3.Апроксимація узагальненими поліномами
Постановка задачі
Припустимо,
що в результаті інженерного або наукового
експерименту отримана система точок:
.
Необхідно знайти аналітичну функцію виду:
, (6.9)
таку що середне квадратичне відхилення цієї функції від заданої системи точок буде мінімальним:
,
(6.10)
Розв’язання
цієї задачі зводиться до знаходження
коефіцієнтів аналітичної функції
.
Визначимо відхилення аналітичної
функції
від експериментальних даних в кожної
i-ої
точці
:
, (6.11)
З
виразу (6.10) видно, що
залежит
від коефіцієнтів
,
тобто є функцією багатьох параметрів.
З відомо, що умовою оптимуму
багатопараметричної функції є умова
виду:
,
(6.12)
підставимо
в (6.12) замість
вираз(6.11) для всіх
і визначимо частинні похідні в виразу
(6.12) по кожному коефіцієнту
.
В результаті отримуємо систему рівнянь
виду:
,
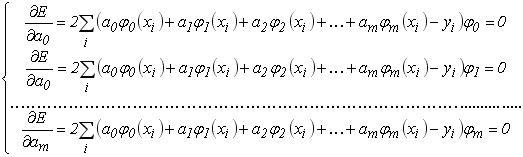(6.13)
Після спрощення та рокриття дужек в кожному рівнянні система (6.13) буде мати вигляд:
,
(6.14)
В матричній формі система (6.14) має вигляд:
,
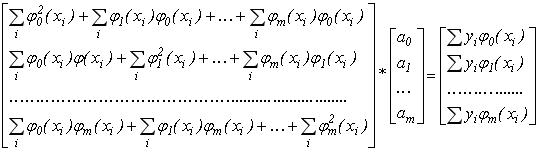(6.15)
Вибір системи функцій здійснюється з врахуванням наявності в експериментальних даних деяких тенденций, наприклад, періодичність експериментальних даних, або експоненціальний або логарифмічний характер їх зміни, властивості симетрії або наявність асимптотики.
4.Апроксимація ортогональними поліномами
Розглянемо спочатку поняття ортогональності та ортогональних функцій або системи функцій.
Функції
і
називаються
ортогональними
на заданій множині точок
,
якщо сума попарних добутків цих функцій
= 0.
,
(6.16)
Система
функцій
називається
ортогональною
на заданій множині точок
, якщо сума попарних добутків цих функцій
дорівнює нулю, виключаючи добуток
функції саму на себе.
,
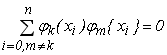(6.17)
Величина
=
називається нормою
системи функцій
.
Якщо для заданої системи функцій на заданій множині точок норма дорівнює одиниці, то така система функцій називається ортонормованою.
Якщо система функцій на заданій множині точок ортогональна і норма системи функції більше 0, то така система функції називається лінійно незалежною.
Розглянемо математичні моделі апроксимації табличних функцій ортогональним поліномом.
Постановка задачі апроксимації
В
результаті інженерного експерименту
отримана система точок
.
Необхідно знайти аналітичну функцію вигляду
, (6.18)
яка
найкращим чином описує задану систему
точок і забезпечує суму квадратів
відхилень аналітичної функції
від
експериментальної на заданій множині
.
Тут
- задана система функций,
- коефіціенти поліному.
Для розв’язування цієї задачі використовують метод найменших квадратів( МНК), який дозволяє звести задачу до двох:
- пошук
коефіцієнтів апроксимуючої функції
;
- пошук
оптимальної кількості ортогональних
функції
.
Для пошуку коефіцієнтів апроксимації використовують критерій СКВ:
за
допомогою якого будують систему лінійних
алгебраїчних рівнянь відносно невідомих
коефіцієнтів
виду:
.(6.19)
Якщо в
якості системи функцій
вибрати
ортогональну систему функцій, то матриця
коефіцієнтів перетворюється в діагональну
матрицю, тобто в матрицю, в якої всі
елементи дорівнюють 0, відповідно умові
ортогональності (6.17), крім діагональних
елементів ( для яких виконується умова
).
В цьому випадку в системі лінійних
алгебраїчних рівнянь (6.19) кожне рівняння
системи має тільки один невідомий
коефіцієнт,
тому
для знаходження коефіцієнтів апроксимуючого
поліному
не треба розв’язувати системи лінійних
алгебраїчних рівнянь а достатньо знайти
їх за формулою:
. (6.20)
Якщо умова ортогональності задовольняє умовам експерименту, то потрібно вибрати апроксимуючий ортогональний поліном або з таблиці 6.1 або з довідників спеціальних функций.
Пошук
оптимальної
кількості m
функцій
не потребує повторного обчислення
коефіцієнтів поліному, тобто кожний
новий коефіцієнт залежить тільки від
заново вибраної функції
. Ця властивість є перевагою метода
апроксимації табличної функції
ортогональними поліномами, тому що в
методі апроксимації табличної функції
степеневими поліномами при пошуку
оптимального степеня поліному потрібно
обчислення всіх коефіцієнтів
заново
при кожному новому значенні m.
Висновок. В порівнянні з апроксимацією табличних функцій степеневими функціями - ортогональні поліноми спрощують задачу апроксимації, зменшують кількість обчислювальних операцій і дозволяють визначити коефіцієнти апроксимуючої функції без розв’язування СЛАР методом Гауса.