2. Розробка алгоритмів та вибір оптимального алгоритму

При розробці алгоритму обчислення значення функції за допомогою інтерполяційної формули Бесселя будемо використовувати формулу яка описана в теоретичних відомостях.

Аналіз формули та прикладу, наведеного в першому розділі, показує що для обчислення значення функції необхідно обчислити значеня кінцевих різниць а також значеннь q та р. Безпосереднє обчислення за формулою вимагає операцій додавання (віднімання), n - операцій ділення та - операцій множення. З врахуванням того, що час виконання операції множення та ділення відповідно в 1,14 та 2,33 рази більший за час виконання операції додавання (віднімання) при використанні математичного співпроцесора, загальна кількість операцій обчислення складає

Алгоритм можна побудувати таким чином, щоб спочатку обчислити всі всі знаменники поліному, а потім провести обчислення за основною формулою. В цьому випадку необхідно комірок пам’яті.

Інший спосіб побудови алгоритму полягає в тому, щоб проводити обчислення знаменників поліному одночасно з обчисленнями за основною формулою виходячи з факторіалу. В цьому випадку для збереження значень необхідно лише n-1 комірок пам’яті.

Комплексний коефіцієнт ефективності Ке одного алгоритму в порівнянні з іншим можна обчислити за формулою

де К_ч – коефіцієнт ефективності за часом виконання;

К_m – коефіцієнт ефективності за затратами пам’яті алгоритму.

Оскільки коефіцієнт ефективності за часом виконання алгоритму можна приблизно оцінити за кількістю арифметичних операцій алгоритму, то комплексний коефіцієнт ефективності описаних вище алгоритмів складає

Для випадку коли n=9

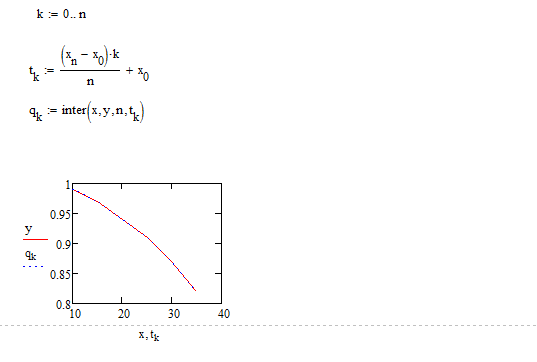
Блок-схеми описаних вище алгоритмів відповідно на рис 2.1 та рис 2.2. В даних алгоритмах вважається, що матриця A використовуються для збереження таблиці різниць, значення x, x0, n, q – однойменні змінні [6].

РОЗДІЛ 8

АПРОКСИМАЦІЯ ЕКСПЕРЕМЕНТАЛЬНИХ ДАНИХ

1.Апроксимація табличних функцій

Інженеру звичайно приходиться працювати з великими масивами даних, тому методи обробки числових даних мають для нього особливе значення. Часто шляхом к правильному розумінню багатьох задач служить продумане уявлення початкових даних. До речі невдале уявлення експериментальних даних буває причиною помилок в розв’язанні складних задач.

Для того щоб отримати аналітичні залежності, що описують великі масиви даних, використовують методи апроксимації, які основані на тому, що масив даних замінюють простою функцією (лінійною або квадратичною або кубічною або іншою), яка не обов’язково проходить через всі експериментальні точки, але описує тенденції зміни цих даних та забезпечує мінімум суми квадратів відхилень експериментальних даних від цією функції.

Постановка задачі

Припустимо, що в результаті інженерного або наукового експерименту отримана система точок . Необхідно знайти аналітичну залежність , таку, яка найкращим чином описує задану систему точок. Поняття "найкращим чином" означає розв’язання задачі по заданому критерію. Найбільш відомим критерієм для задач апроксимації є критерій середньоквадратичних відхилень (СКВ), який являє собою мінімізацію суми квадратів відхилень експериментальних даних від аналітичної функції і визначається на заданій множині точок як

.

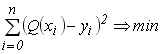Однак при такій постановці задача апроксимації експериментальних даних має багато розв’язків. Для отримання єдиного розв’язку цієї задачі потрібно задавати значення певного вигляду, наприклад:

• степеневим поліномом ; 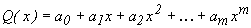(6.1)

• тригонометричним поліномом ; 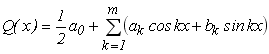(6.2)

• ортогональним поліномом ; 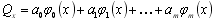(6.3)

• сплайн-функцією та інш.