3.4. Преобразование полосы для цифровых фильтров

По аналогии с фильтрами непрерывного времени существует несколько простых преобразований цифрового фильтра нижних частот (с частотой среза w_c) в другой фильтр нижних частот (с другой частотой среза w_u), а также в цифровой фильтр верхних частот, полосовой или режекторный. Далее приведены формулы для этих преобразований.

1. Фильтр нижних частот фильтр нижних частот:

,

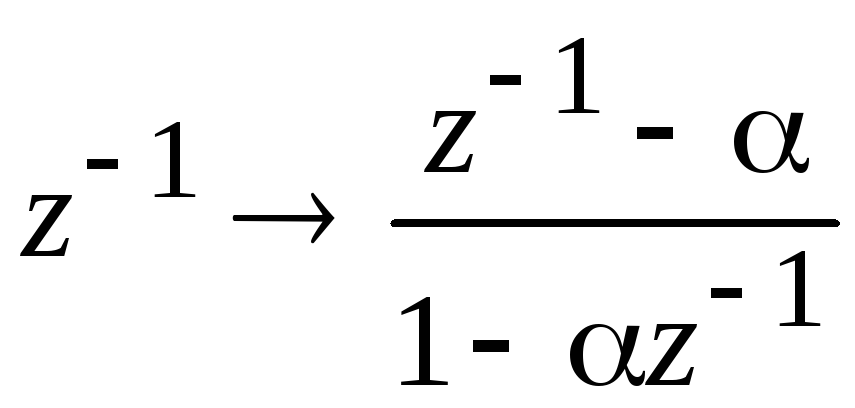где 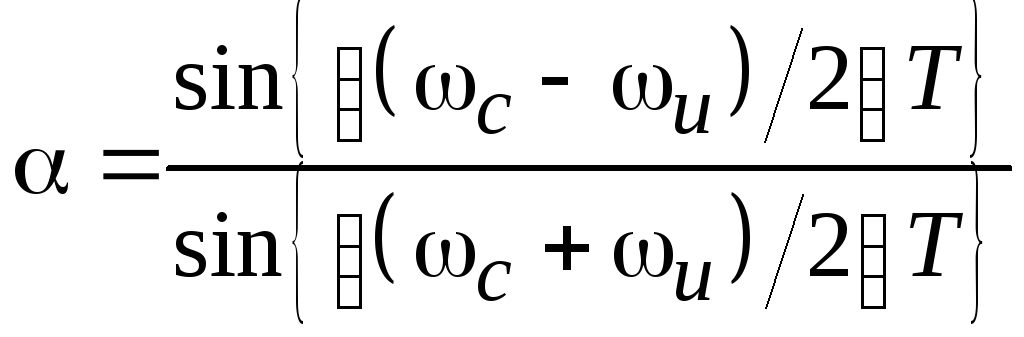;w_u – заданная частота среза фильтра нижних частот.

8. Фильтр нижних частот  фильтр верхних частот:

,

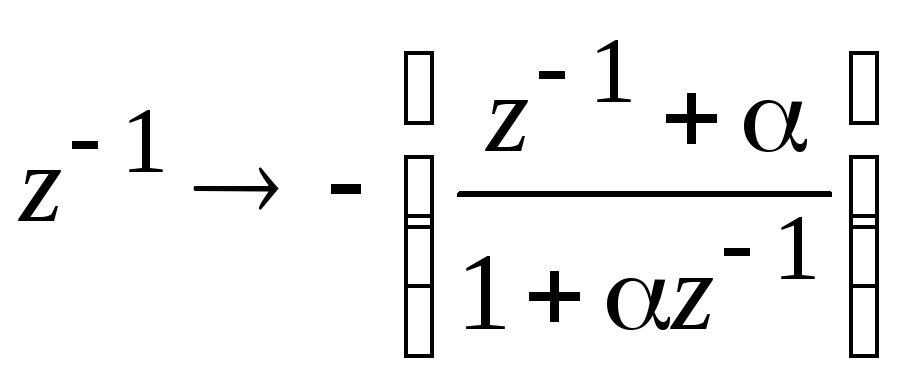где 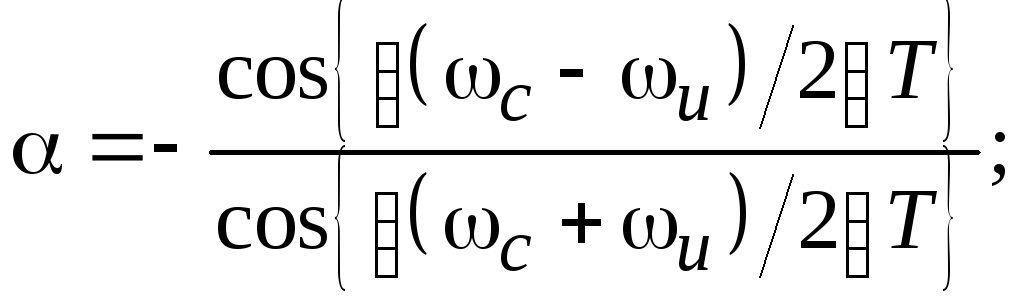w_u – заданная частота среза фильтра верхних частот.

9. Фильтр нижних частот  полосовой фильтр:

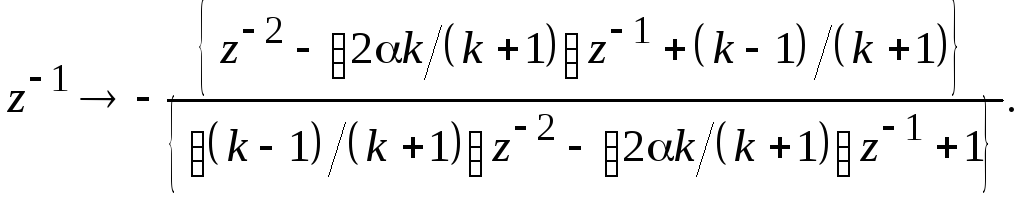
Здесь 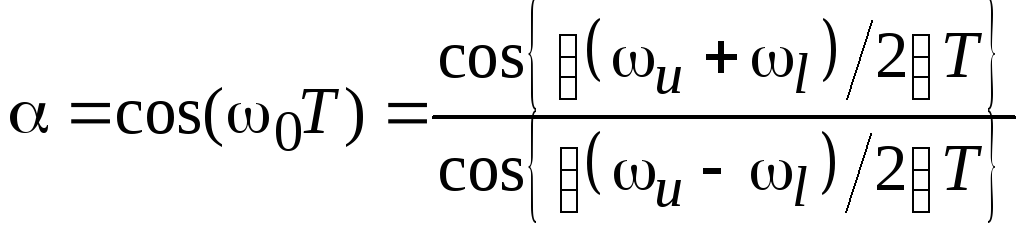;;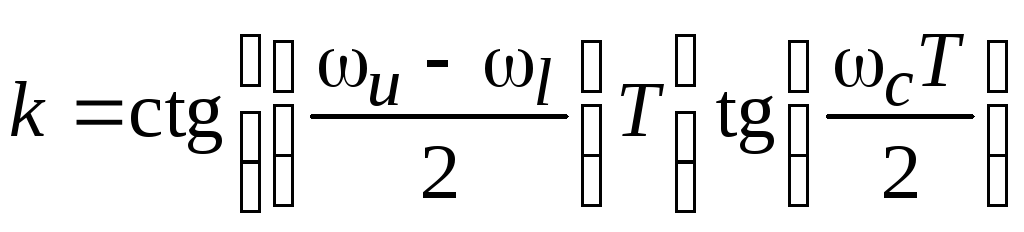w₀ – центральная частота полосового фильтра.

10. Фильтр нижних частот  режекторный фильтр:

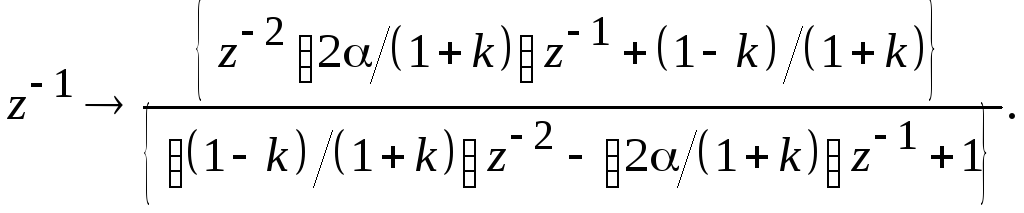
Здесь 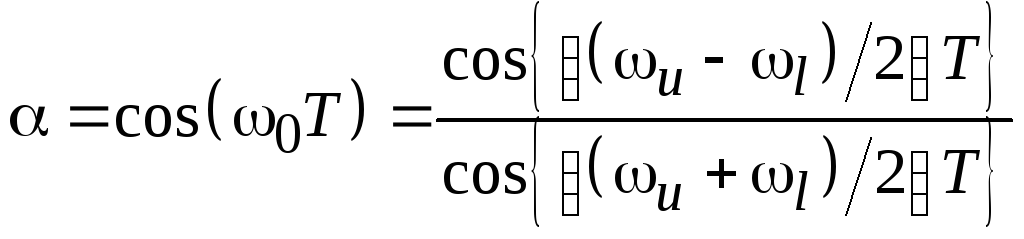; ; w₀ – центральная частота режекторного фильтра.

4. Методы реализации цифровых фильтров

Цифровые фильтры с заданной передаточной функцией можно построить различными способами. В любом реальном фильтре шумы и погрешности, появляющиеся при квантовании, существенно зависят от структуры фильтра. Прежде всего все фильтры можно разделить на два больших класса:

• рекурсивные;

• нерекурсивные.

Для рекурсивных фильтров соотношение между входной последовательностью {x(n)} и откликом фильтра {y(n)} может быть записано следующим образом: т. е. текущий отсчет отклика y(n) определяется не только текущим и предшествующим значениями входной последовательности, но и предшествующими отсчетами отклика.

В нерекурсивных фильтрах связь между входной последовательностью и откликом имеет вид , т. е. текущий отсчет отклика зависит от текущего и предшествующих значений входной последовательности.

Реализация может осуществляться на основе следующих форм построения схем фильтра:

• прямой;

• канонической прямой;

• каскадной;

• параллельной.

4.1. Прямая форма

Рассмотрим передаточную функцию N-го порядка вида

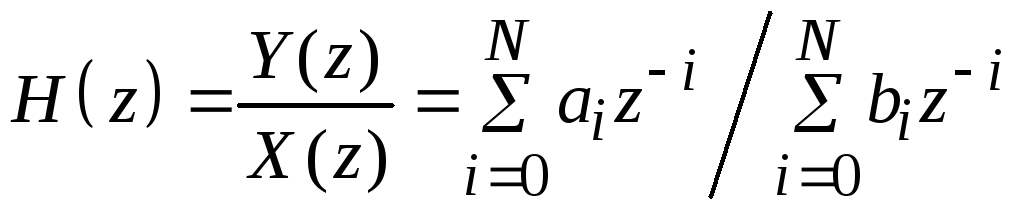, (4.1)

причем b₀ = 1. Приведя это равенство к общему знаменателю, получим:

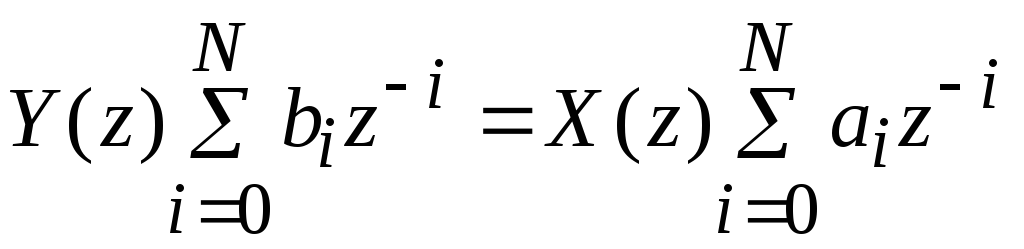
или

.

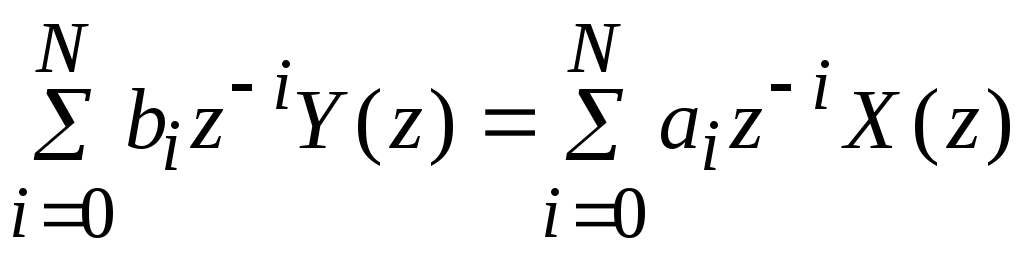Если рассматривать члены вида z^–kY(z) как обратные z-преобразования последовательностей y(n – k), то, взяв обратные z-преобразования обеих частей последнего равенства, можно получить искомое разностное уравнение

.

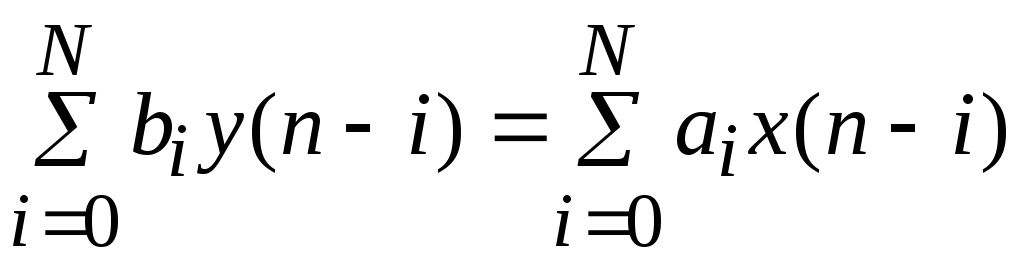Поскольку b₀ = 1, разностное уравнение можно решить относительно y(n):

.

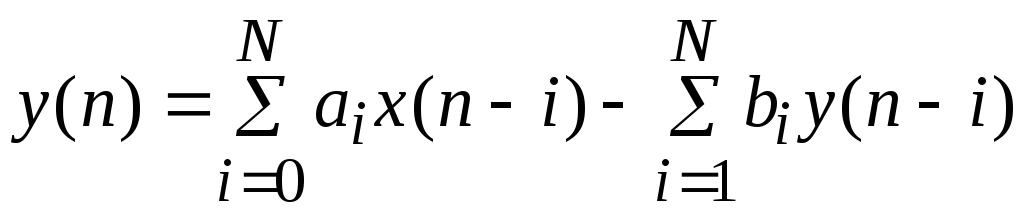Простая структура реализации данного разностного уравнения, называемая прямой формой, показана на рис. 4.1.

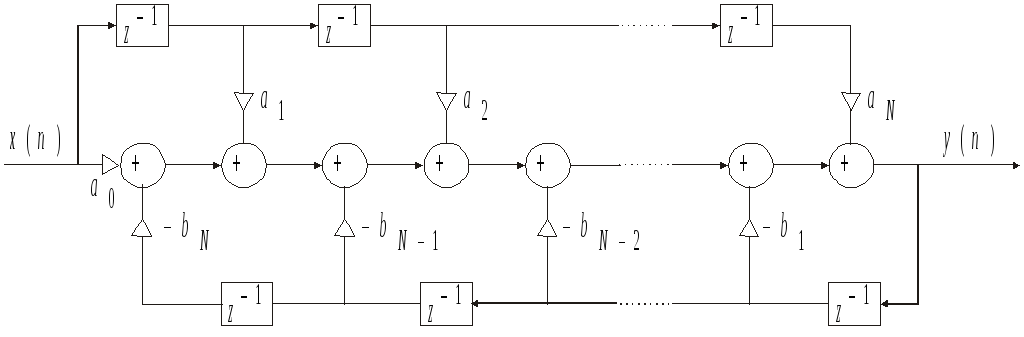
Рис. 4.1

В ней для образования цепей используются раздельные элементы задержки. Характерными чертами этой структуры являются ее простота и непосредственная связь с z-преобразованием. Однако эта структура очень чувствительна к квантованию коэффициентов.

4.2. Прямая каноническая форма

Запишем формулу (4.1) в следующем виде:

.

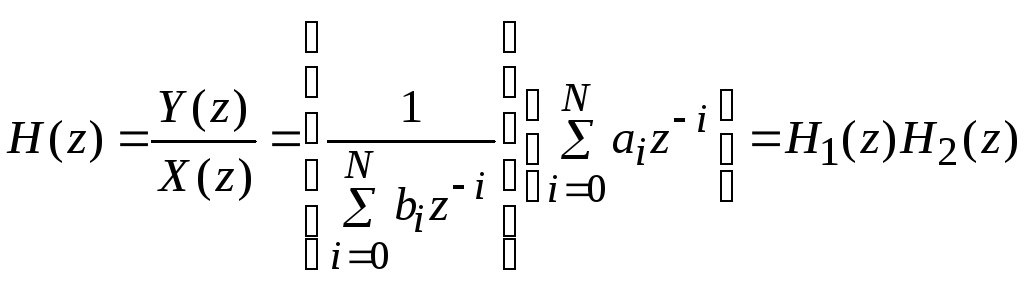Цифровой фильтр, соответствующий этой формуле, состоит из двух последовательно соединенных фильтров с коэффициентами передачи, соответственно, H₁(z) и H₂(z). Первый фильтр имеет только полюсы, а второй – только нули. Если записать

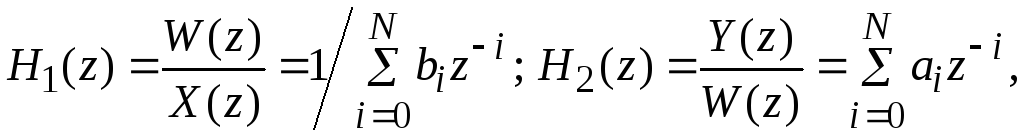
то получится пара разностных уравнений (в предположении, что b₀ = 1)

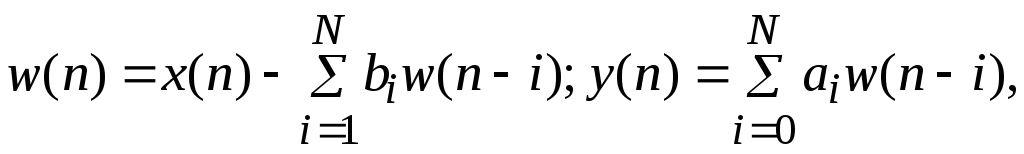
которые можно реализовать, как показано на рис. 4.2.

Рис. 4.2

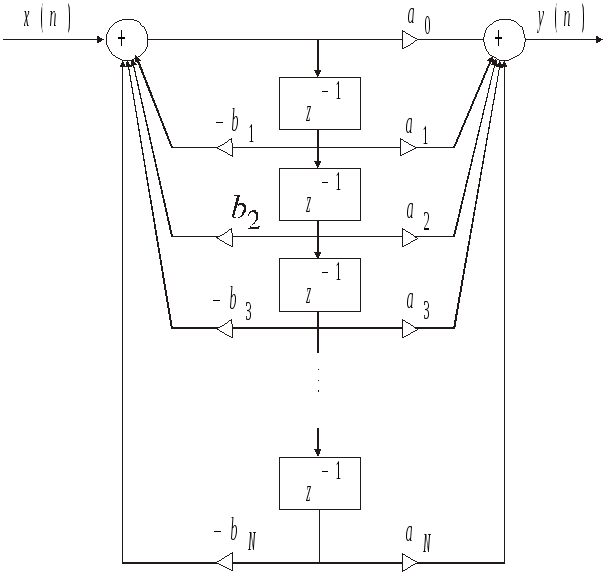
Рис. 4.3

Поскольку в цепях, соответствующих H₁(z) и H₂(z), сигнал w(n) задерживается одинаково, то для построения фильтра достаточно использовать один набор элементов задержки (рис. 4.3). Такую структуру называют канонической формой, так как в ней используется минимальное количество сумматоров, умножителей и элементов задержки.