2.1. Прямоугольное окно

N-точечное прямоугольное окно соответствует простому усечению ряда Фурье. Оно описывается весовой функцией:

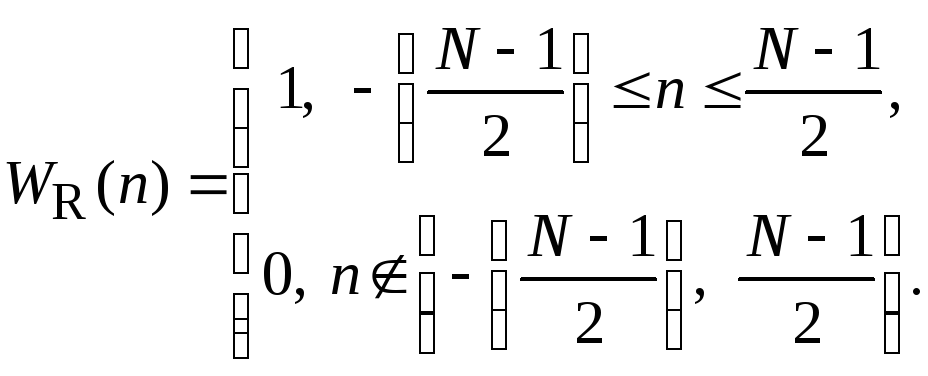
Частотная характеристика прямоугольного окна описывается соотношением

.

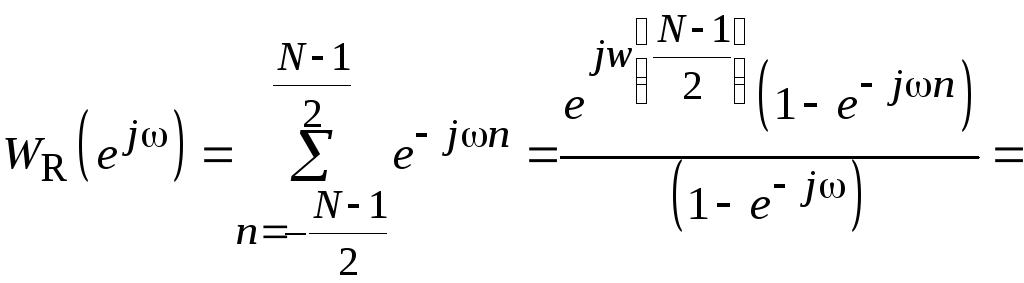
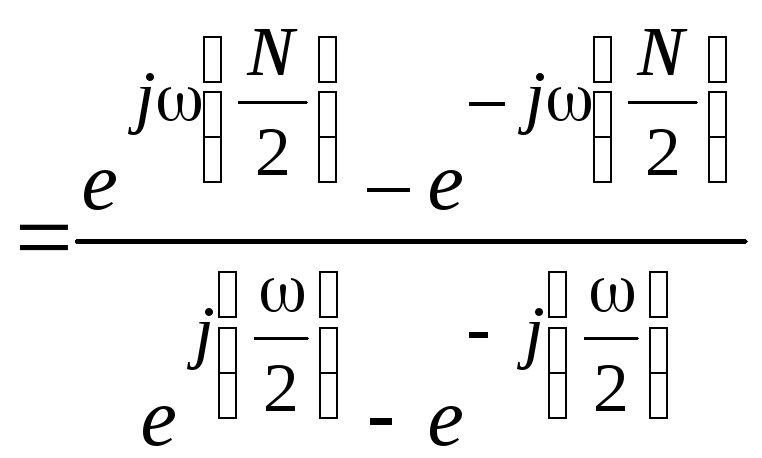Таким образом,

.

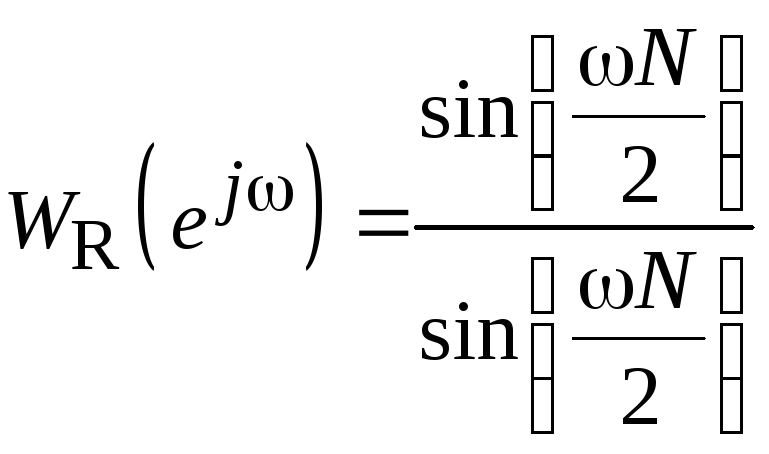2.2. Обобщенное окно Хэмминга

Формула обобщенного окна Хэмминга имеет вид

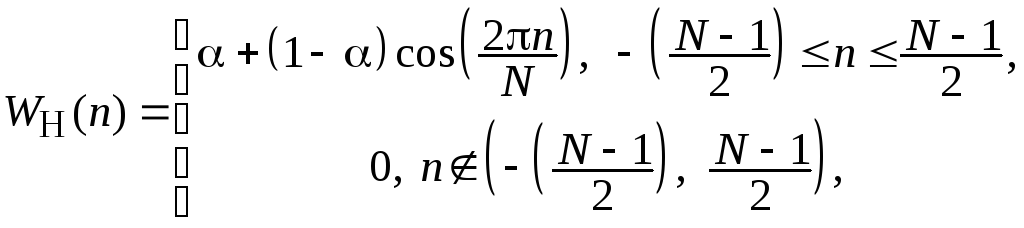
причем, лежит в пределах 0£ a £ 1. Случай = 0.5 соответствует окну Ханна, а случай= 0.54 – окну Хэмминга.

Обобщенное окно Хэмминга для всех n может быть представлено в виде формулы

.

Следовательно, частотная характеристика обобщенного окна Хэмминга равна круговой свертке частотной характеристики прямоугольного окна с последовательностью импульсов и может быть записана в виде

,

откуда

.

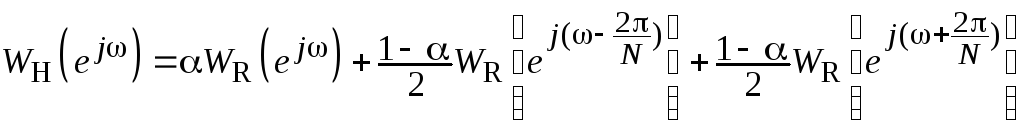Ширина главного лепестка частотной характеристики окна Хэмминга в два раза больше, чем для прямоугольного окна. Уровень боковых лепестков в случае окна Хэмминга значительно ниже, чем у характеристики прямоугольного окна. Боковые лепестки функций 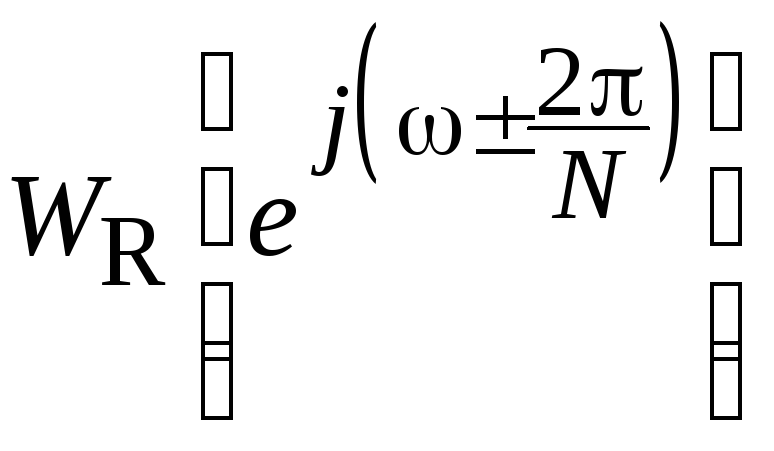находятся в противофазе с боковыми лепестками, поэтому общий уровень боковых лепестков значительно уменьшается.

2.3. Окно Блэкмана

Функция окна Блэкмана подобна функциям окон Ханна и Хэмминга и определяется выражением

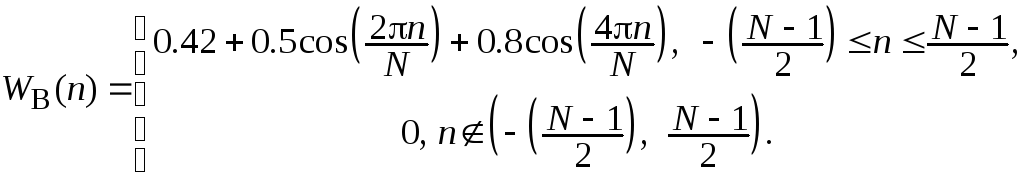
Дополнительный косинусоидальный компонент обеспечивает еще более значительное уменьшение пульсаций Гиббса. Ширина главного лепестка увеличивается и оказывается в три раза больше, чем у прямоугольного окна.

2.4. Окно Кайзера

Задача расчета хороших окон фактически сводится к математической задаче отыскания ограниченных во времени функций, преобразование Фурье которых наилучшим образом аппроксимируют функции, ограниченные по частоте, т. е. имеющие минимальную энергию за пределами заданного интервала частот. При решении этой задачи в замкнутой форме для непрерывных функций времени был выведен класс так называемых вытянутых сфероидальных волновых функций. Эти функции имеют достаточно сложный вид, поэтому Кайзер в качестве наилучшего окна предложил относительно простую аппроксимацию этих функций. Эта аппроксимация, названная окном Кайзера, имеет вид

,

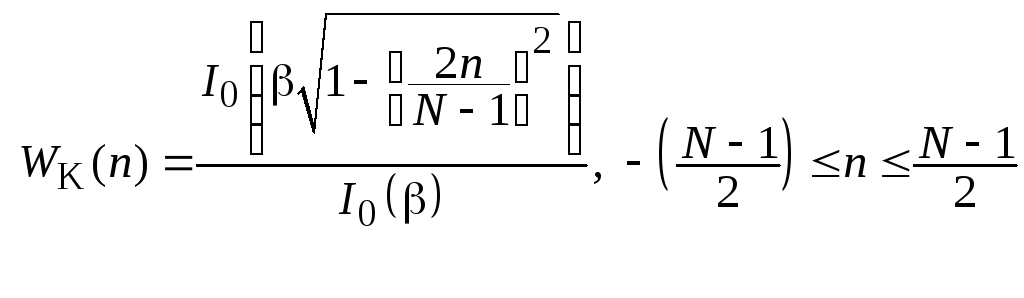где b – константа, определяющая компромисс между максимальным уровнем боковых лепестков и шириной главного лепестка (или долей энергии в главном лепестке) частотной характеристики окна; I₀(x) – функция Бесселя нулевого порядка.

Частотная характеристика дискретного окна Кайзера в замкнутой форме не получена, но Кайзер показал, что для непрерывной функции окна частотная характеристика пропорциональна

,

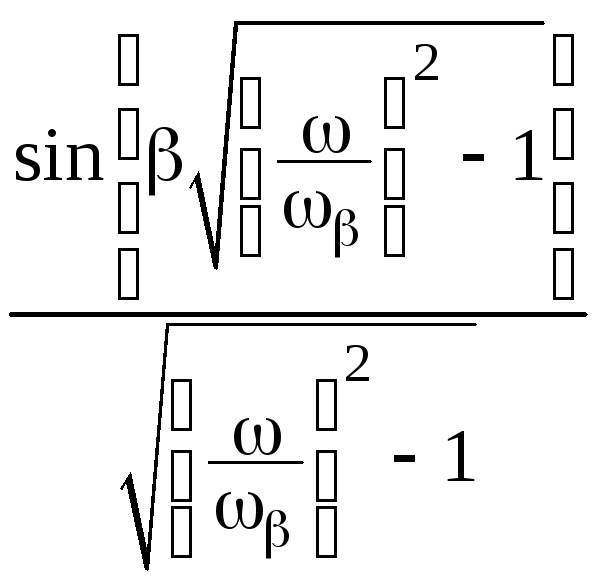где величина w_b приблизительно равна ширине главного лепестка частотной характеристики.

Окно Кайзера является, по существу, оптимальным окном в том смысле, что оно представляет собой последовательность конечной длины, которая имеет минимум энергии спектра за пределами некоторой заданной частоты.

3. Бих-фильтры. Методы синтеза

Фильтром с бесконечной импульсной характеристикой (БИХ-фильтром) называют фильтр, длина импульсной характеристики которого не ограничена справа или слева.

Будем рассматривать БИХ-фильтры при условии, что они являются физически реализуемыми и устойчивыми. Для импульсных характеристик таких фильтров h(n) справедливы следующие ограничения:

Наиболее общая форма записи z-преобразования импульсной характеристики БИХ-фильтров имеет вид

.

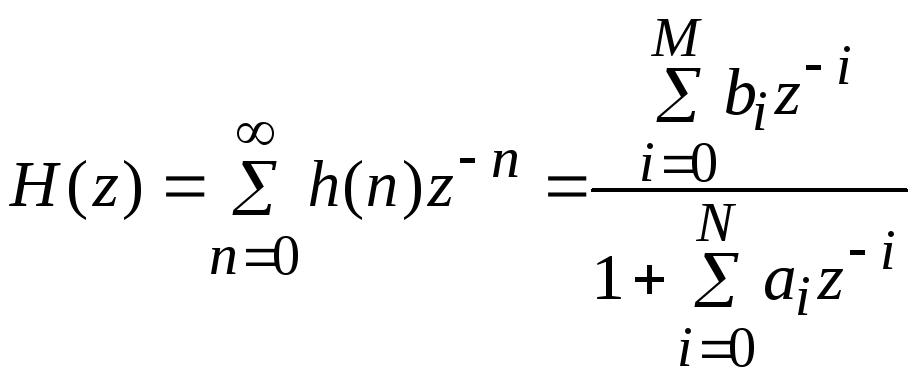Предположим, что M £ N. Системы, удовлетворяющие этому условию, называют системами N-го порядка.

Решение задачи расчета фильтров сводится к нахождению значений его коэффициентов a_i и b_i, обеспечивающих аппроксимацию заданных характеристик фильтра. Таким образом, задача расчета фильтра в значительной степени сводится к задаче аппроксимации и может быть решена чисто математическими методами.

Наиболее распространенным методом расчета цифровых БИХ-фильтров является метод дискретизации аналогового фильтра, удовлетворяющего заданным требованиям. При расчете цифровых фильтров верхних частот, полосовых и режекторных, используются два подхода, представленные на рис. 3.1

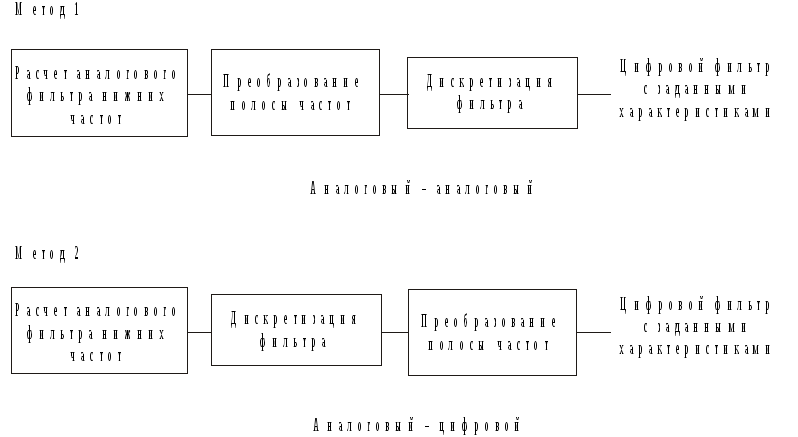
Рис. 3.1

В первом случае нормализованный аналоговый фильтр предварительно преобразуется в другой аналоговый фильтр, из которого путем дискретизации рассчитывается фильтр с заданными характеристиками. Во втором случае нормализованный фильтр нижних частот дискретизуется сразу же, а затем преобразованием его полосы частот формируется цифровой фильтр с заданными характеристиками.