Freqs – частотная характеристика аналогового фильтра:

H = FREQS(B,A,W) возвращает вектор H (комплексный частотный отклик) фильтра B/A

.

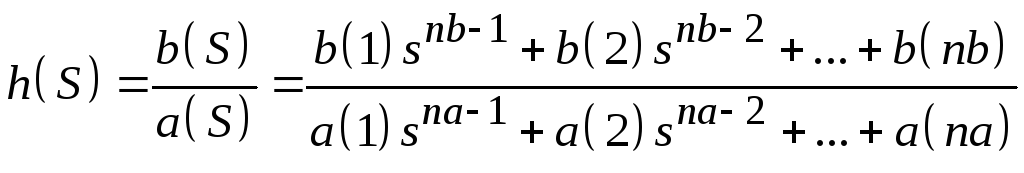Частотный отклик имеет значения в точках вектора W. Амплитуда и фаза могут быть получены вызовом FREQS(B,A,W) без выходных параметров.

[H,W] = FREQS(B,A) автоматически выбирает значение частоты 200, на котором и вычисляется частотная характеристика.

FREQS(B,A,N) выбирает N частот.

Смотри также LOGSPACE, POLYVAL, INVFREQS и FREQZ.

Freqspace – формирование последовательности отсчетов частоты:

FREQSPACE возвращает последовательности отсчетов частоты.

FREQSPACE полезна для получения желаемых частотных ответов для FSAMP2, FWIND1 и FWIND2 так же, как для различных 1D-приложений.

[F1,F2] = FREQSPACE(N) возвращает 2D-частотный диапазон векторов F1 и F2 для матрицы размером NN.

[F1,F2] = FREQSPACE([M N]) возвращает 2D-частотный диапазон векторов для матрицы MN.

Для 2D-векторов и n нечетного F = (–1+1/n: 2/n: 1–1/n).

Для 2D-векторов и n четного F = (–1 : 2/n: 1–2/n).

[F1,F2] = FREQSPACE(...,'meshgrid') – эквивалентно [F1,F2] = freqspace(...); [F1,F2] = meshgrid(F1,F2);

F = FREQSPACE(N) возвращает 1D-частотный вектор F, предполагающий наличие N интервалов на единичной окружности. Для 1D-векторов F= (0 : 2/n : 1). F = FREQSPACE(N,'whole') возвращает все N интервалов, поэтому F = (0 : 2/n : 2(n – 1)/n).

Смотри также FSAMP2, FWIND1, FWIND2.

Freqz – частотная характеристика цифрового фильтра.

Когда N целое, [H,W] = FREQZ(B,A,N) возвращает для вектора частот W в радианах N-точечную комплексную частотную характеристику в векторе H фильтра B/A:

.

Частота отклика оценивается в N точках одинаково расположенных интервалов верхней половины единичной окружности. Если N не определено, то по умолчанию равно 512.

[H,W] = FREQZ(B,A,N,'whole') использует N точек по всей окружности.

H = FREQZ(B,A,W) возвращает частоту отклика на частотах, назначенных в векторе W, в радианах (нормально между 0 и ).

[H,F] = FREQZ(B,A,N,Fs) и [H,F] = FREQZ(B,A,N,'whole',Fs) на заданной частоте дискретизации Fs (в герцах) возвращают вектор частот F (в герцах).

H = FREQZ(B,A,F,Fs) на заданной частоте дискретизации Fs (в герцах) возвращает комплексную частоту ответа на частотах, определенных в векторе F (в герцах).

FREQZ(B,A,...) без выходных аргументов рисует амплитуду и развернутую частоту B/A в текущем графическом окне.

Смотри также FILTER, FFT, INVFREQZ, FREQS и GRPDELAY.

Grpdelay – групповая задержка цифрового фильтра:

[Gd,W] = GRPDELAY(B,A,N) возвращает N-мерные вектора Gd и W, содержащие групповую задержку и частоты (в радианах), на которых будет производиться оценка. Групповая задержка определяется как производная – d{angle(w)}/dw. Частота отклика оценивается в N точках, равномерно расположенных на верхней половине единичной окружности. Когда N – степень 2, то вычисления производятся быстрее с использованием FFT. Если вы не определили N, то по умолчанию оно равно 512.

GRPDELAY(B,A,N,'whole') использует N точек по всей окружности.

[Gd,F] = GRPDELAY(B,A,N,Fs) и [Gd,F] = GRPDELAY(B,A,N,'whole',Fs) на заданной частоте дискретизации Fs (в герцах) возвращает вектор F (в герцах).

Gd = GRPDELAY(B,A,W) и Gd = GRPDELAY(B,A,F,Fs) возвращают задержку группы, оцениваемую в точках W (в радианах) или F (в герцах), где Fs – частота дискретизации (в герцах).

GRPDELAY(B,A,...) без выходных аргументов рисует задержку группы как функцию нормализованной частоты (Nyquist == 1) в текущем графическом окне.

Смотри также FREQZ.