Министерство образования РФ

______________________

Санкт-Петербургский государственный электротехнический

университет "ЛЭТИ"

______________________

А. В. Бадейкин В. В. Геппенер И. А. Корнеев

СИНТЕЗ ЦИФРОВЫХ ФИЛЬТРОВ

С ИСПОЛЬЗОВАНИЕМ ПАКЕТА ПРОГРАММ MATLAB

Учебное пособие

Санкт-Петербург

Издательство СПбГЭТУ "ЛЭТИ"

2001

УДК 621.372.542

ББК 3.973.233–018я7

Б15

Бадейкин А. В., Геппенер В. В., Корнеев И. А. Cинтез цифровых фильтров c использованием пакета программ MATLAB: Учеб. пособие. СПб.: Изд-во СПбГЭТУ "ЛЭТИ", 2001. 72 с.

Содержит основные теоретические сведения о методах синтеза цифровых фильтров. Рассмотрены вопросы использования пакета MATLAB для решения задач синтеза цифровых фильтров на ПЭВМ. Приведены основные сведения по базовым функциям, используемым в задачах синтеза цифровых фильтров. Приведены примеры расчета цифровых фильтров различного типа.

Предназначено для студентов специальности 220400 "Программное обеспечение вычислительной техники и автоматизированных систем".

Рецензенты: кафедра "Радиоэлектронные системы управления" (БГТУ "Военмех" им. Д. Ф. Устинова); канд. техн. наук Н. А. Федоров (ОАО "Радиоавионика").

Утверждено

редакционно-издательским советом университета

в качестве учебного пособия

ISBN 5-7629-0404-0 © СПбГЭТУ "ЛЭТИ", 2001

1. Общая характеристика цифровых фильтров

Различают два общих класса сигналов: аналоговые и дискретные. Аналоговым сигналом называется сигнал, определенный для каждого момента времени, дискретным сигналом – сигнал, определенный только в дискретные моменты времени. Как дискретный, так и аналоговый сигналы могут быть однозначно представлены некоторыми функциями частоты, которые называются их частотными спектрами.

Фильтрацией называется процесс изменения частотного спектра сигнала в некотором желаемом направлении. Этот процесс может привести к усилению или ослаблению частотных составляющих в некотором диапазоне частот, к подавлению или выделению какой-нибудь конкретной составляющей и т. п.

Цифровым фильтром называется цифровая система, которую можно использовать для фильтрации дискретных сигналов. Он может быть реализован программным методом или с помощью специальной аппаратуры, и в каждом из этих случаев цифровой фильтр можно применить для фильтрации сигналов как в реальном времени, так и предварительно записанных.

Цифровой фильтр можно представить структурной схемой, изображенной на рис. 1.1. На этой схеме x(n) и y(n) – соответственно, входное воздействие и реакция фильтра на это воздействие. Функционально они связаны соотношением

,

где вид оператора зависит от свойств конкретной системы.

Рис. 1.1

Реакцию цифрового фильтра на произвольное воздействие можно представить с помощью импульсной характеристики фильтра. Допустим, что x(n) – входная, а y(n) – выходная последовательности фильтра и пусть h(n) – отклик на единичный импульс, называемый импульсной характеристикой. Тогда

.

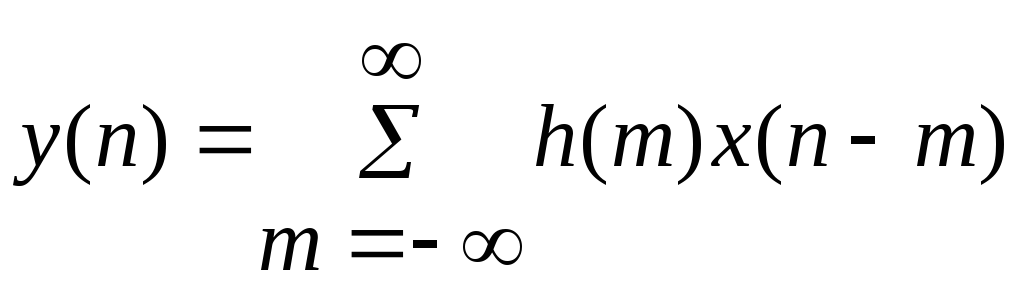Таким образом, x(n) и y(n) связаны соотношением типа свертки. Частотная характеристика фильтра определяется следующим выражением:

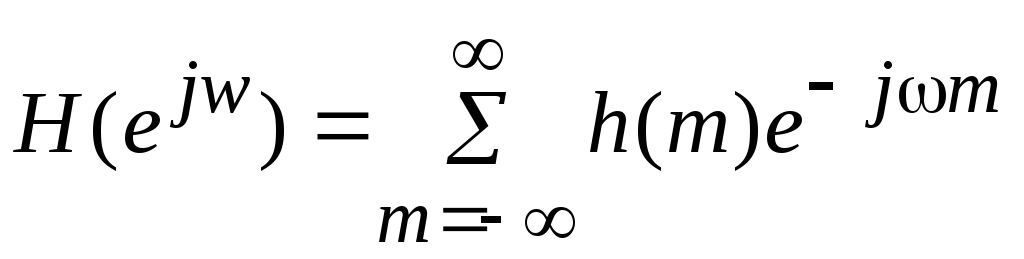. (1.1)

Поскольку частотная характеристика является периодической функцией частоты , равенство (1.1) можно рассматривать как разложение в ряд Фурье, причем коэффициенты являются одновременно отсчетами импульсной характеристики. Согласно теории рядов Фурье, коэффициенты h(n) могут быть выражены через :

.

Из этого соотношения видно, что h(n) по существу является суперпозицией синусоид с амплитудами , которые можно представить следующим образом:

.

Выражение называют амплитудной характеристикой фильтра, а – фазовой характеристикой фильтра.

1.1. Свойства цифровых фильтров

Дадим несколько определений, посвященных цифровым фильтрам.

1. Цифровой фильтр называется стационарным, если его параметры не изменяются во времени, т. е. предварительно невозбужденный фильтр, в котором x(n) = y(n) = 0 при всех n < 0, называют стационарным тогда и только тогда, когда 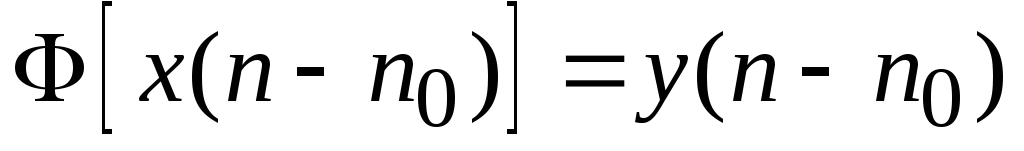для всех возможных воздействий.

2. Цифровой фильтр называют линейным тогда и только тогда, когда 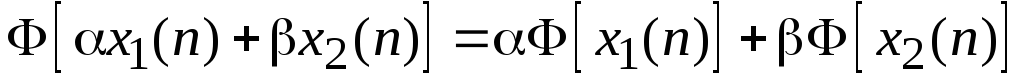для всех a и b – произвольных постоянных и для всех допустимых воздействий x₁(n) и x₂(n).

3. Цифровой фильтр называют физически реализуемым, если величина отклика при n = n₀ зависит только от значений входной последовательности с номерами n £ n₀. Это означает, что импульсная характеристика h(n) равна нулю при n < 0.

4. Цифровой фильтр называется устойчивым тогда и только тогда, когда реакция на ограниченное воздействие ограничена, т. е. если из 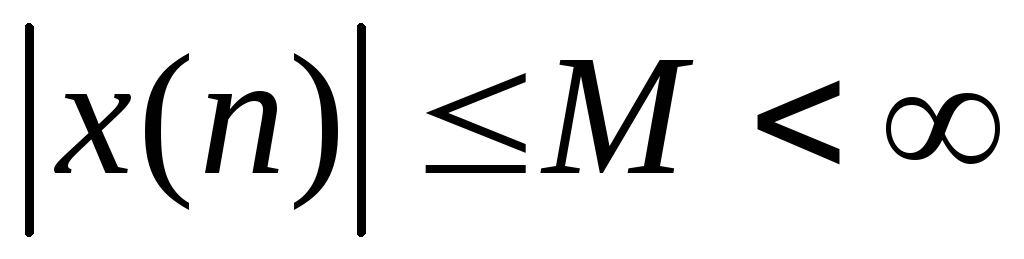при всех n следует 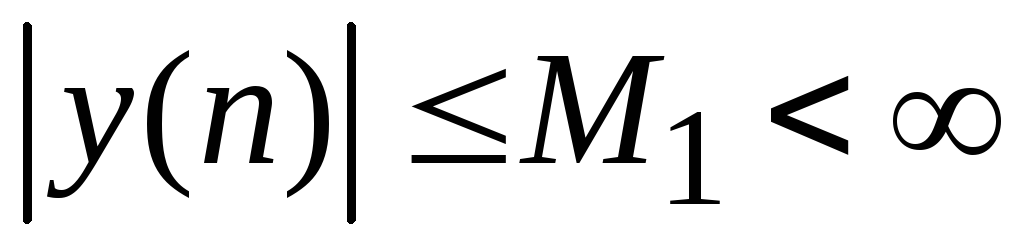при всех n. Необходимым и достаточным условием устойчивости фильтра является следующее требование к его импульсной характеристике:

.
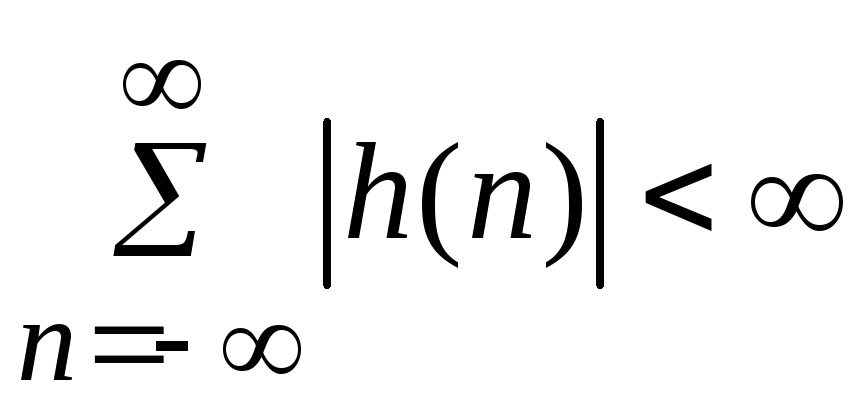