16.Дисперсия появления события а в одном и нескольких независимых испытаниях.

Теорема. Дисперсия числа появлений события А в n независимых испытаниях, в каждом вероятность p появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: D(X)=npq. Доказательство. Рассмотрим случ. величину Х-число появлений события А в n независимых испытаниях. Очевидно, общее число появлений события в этих испытаниях равно сумме появлений события в отдельных испытаниях: Х=Х₁+Х₂+…+Х_n, где Х₁-число наступлений события в первом испытании, Х₂-во втором,…,Х_n-в n-м. Величины Х₁,Х₂,…Х_n взаимно независимы, т. к. исход каждого испытания не зависит от исходов остальных, поэтому мы вправе воспользоваться следствием1: D (Х)= D (Х₁)+ D (Х₂)+…+ D (Х_n). Вычислим дисперсию Х₁ по формуле D(Х₁)=М(Х₁²)-Ї М(Х₁)Ї². Величина Х₁-число появлений события А в первом испытании, потому М(Х₁)= p. Найдем мат. ожидание величины Х₁², которая может принимать только два значения, а именно: 1² с вероят. p и 0² с вероят. q. Подставляя найденные результаты в соотношение имеем D(Х₁)= p- p²= p(1-p)= pq. Очевидно, дисперсия каждой из остальных случ. величин также равна pq. Заменив каждое слагаемое правой части через pq, окончательно получим D(X)=npq.

17.Мат.Ожидание, дисперсия и среднее квадратичное отклонение среднего арифметического одинаково распределенных взаимно независимых случайных величин.

Обозначим через среднее арифметическое рассматриваемых случайных величин-Х. Установим связь между числовыми характеристиками среднего арифметического Х и соответствующими числовыми характеристиками отдельно взятой случайной величины. Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин: М(Х)=а. Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в n раз меньше дисперсии D каждой из величин: D(Х)= D/ n. Среднее квадратическое отклонение среднего арифметического одинаково распределенных взаимно независимых случайных величин в раз среднего квадратического отклонения 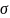каждой из величин: .

18. Закон больших чисел Практика изучения случайных явлений показывает, что хотя результаты отдельных наблюдений, даже проведенных в одинаковых условиях, могут сильно отличаться, в то же время средние результаты для достаточно большого числа наблюдений устойчивы и слабо зависят от результатов отдельных наблюдений. Теоретическим обоснованием этого замечательного свойства случайных явлений является закон больших чисел. Названием "закон больших чисел" объединена группа теорем, устанавливающих устойчивость средних результатов большого количества случайных явлений и объясняющих причину этой устойчивости.

Простейшая форма закона больших чисел, и исторически первая теорема этого раздела - теорема Бернулли, утверждающая, что если вероятность события одинакова во всех испытаниях, то с увеличением числа испытаний частота события стремится к вероятности события и перестает быть случайной. Теорема Пуассона утверждает, что частота события в серии независимых испытаний стремится к среднему арифметическому его вероятностей и перестает быть случайной.

Предельные теоремы теории вероятностей, теоремы Муавра-Лапласа объясняют природу устойчивости частоты появлений события. Природа эта состоит в том, что предельным распределением числа появлений события при неограниченном возрастании числа испытаний (если вероятность события во всех испытаниях одинакова) является нормальное распределение.

Центральная предельная теорема объясняет широкое распространение нормального закона распределения. Теорема утверждает, что всегда, когда случайная величина образуется в результате сложения большого числа независимых случайных величин с конечными дисперсиями, закон распределения этой случайной величины оказывается практически нормальным законом.Теорема, приведенная ниже под названием "Закон больших чисел" утверждает, что при определенных, достаточно общих, условиях, с увеличением числа случайных величин их среднее арифметическое стремится к среднему арифметическому математических ожиданий и перестает быть случайным.

Закон больших чисел. Если случайные величины  ₁,  ₂, …,  _n, … попарно независимы и ,то для любого  > 0

19. интегральная функция распределения и ее свойства. Пример:интегральная функция распределения дискретной случайной величины. Вероятность попадания случайной величины в заданный промежуток.Интегральной функцией распределения называют функцию F(x), определяющую для каждого значения x случайной величины X вероятность того, что величина X примет значение, меньшее x, то есть F(x) = P(X < x).Распределение вероятностей дискретной случайной величины может быть задано перечнем всех ее возможных значений и их вероятностей. Такой способ задания неприменим для непрерывных случайных величин. Общим способом задания распределений любых типов случайных величин является интегральная функция распределения. Пусть x - действительное число. Вероятность события, состоящего в том, что случайная величина X примет значение, меньшее x, то есть вероятность события X < x обозначим через F(x). Интегральной функцией распределения называют функцию F(x), определяющую для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x, то есть F(x) = P(X < x). Интегральная функция распределения имеет следующие свойства. 1. Значения интегральной функции принадлежат отрезку (0,1): 0 і F(x) і 1. Следовательно, график интегральной функции распределения расположен в полосе, ограниченной прямыми y = 0, y = 1. 2. F(x) - неубывающая функция, то есть F(x2) і F(x1), если x2 > x1. Следовательно, при возрастании x в интервале (a, b), в котором заключены все возможные значения случайной величины, график интегральной функции распределения поднимается вверх. 3. Если возможные значения случайной величины принадлежат интервалу (a, b), то F(x) = 0 при a і x, F(x) = 1 при x і b. То есть при a і x ординаты графика интегральной функции распределения равны нулю; при x і b ординаты графика равны единице. Для дискретной случайной величины график интегральной функции распределения имеет ступенчатый вид.

20. Непрерывная случайная величина. Непрерывной случайной величиной (НСВ) называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Множество возможных значений непрерывной случайной величины бесконечно и несчетно.Дифференциальная функция распределения (плотность веро­ятности) f(x) — это первая производная от функции распреде­ления. График функции f(x) называют кривой распределения. Вероятность попадания Х в заданный интервал (a, b) равна Геометрически эта вероятность равна площади криволиней­ной трапеции, ограниченной осью абсцисс, прямыми х = а и х == b и кривой распределения (рис. 1, а). Площадь под всей кривой равна единице.Одним из наиболее часто встречающихся распределений является нормальное распределение. Оно играет большую роль в теории вероятностей и занимает среди других распределений особое положение. Нормальный закон распределения является предельным законом, к которому приближаются другие законы распределения при часто встречающихся аналогичных условиях. Если предоставляется возможность рассматривать некоторую случайную величину как сумму достаточно большого числа других случайных величин, то данная случайная величина обычно подчиняется нормальному закону распределения. Суммируемые случайные величины могут подчиняться каким угодно распределениям, но при этом должно выполняться условие их независимости (или слабой зависимости). При соблюдении некоторых не очень жестких условий указанная сумма случайных величин подчиняется приближенно нормальному закону распределения и тем точнее, чем большее количество величин суммируется. Ни одна из суммируемых случайных величин не должна резко отличаться от других, т. е. каждая из них должна играть в общей сумме примерно одинаковую роль и не иметь исключительно большую по сравнению с другими величинами дисперсию. Для примера рассмотрим изготовление некоторой детали на станке-автомате. Размеры изготовленных деталей несколько отличаются от требуемых. Это отклонение размеров от стандарта вызывается различными причинами, которые более или менее независимы друг от друга. К ним могут относиться: неравномерный режим обработки детали; неоднородность обрабатываемого материала; неточность установки заготовки в станке; износ режущего инструмента и деталей станков; упругие деформаций узлов станка; состояние микроклимата в цехе; колебание напряжения в электросети и т. д. Каждая из перечисленных и подобных им причин влияет на отклонение размера изготовляемой детали от стандарта. Таким образом, общее отклонение размера, фиксируемое измерительным прибором, является суммой большего числа отклонений, обусловленных различными причинами. Если ни одна из этих причин не является доминирующей, то суммарное отклонение является случайной величиной, имеющей нормальный закон распределения. Так как нормальному закону подчиняются только непрерывные случайные величины, то это распределение можно задать в виде плотности распределения вероятности. Определение: Непрерывная случайная величина Х имеет нормальное распределение (распределена по нормальному закону), если плотность распределения вероятности f(x) имеет вид

где а и —некоторые постоянные, называемые параметрами нормального распределения. Функция распределения F(x) в рассматриваемом случае принимает вид

Параметр а- есть математическое ожидание НСВХ, имеющей нормальное распределение,  - среднее квадратическое отклонение, тогда дисперсия равна Выясним геометрический смысл параметров распределения а и . Для этого исследуем поведение функции f(x). График функции f(x) называется нормальной кривой.Рассмотрим свойства функции f(x): 1°. Областью определения функции f(x) является вся числовая ось. 2°. Функция f{x) может принимать только положительные значения, т. е. f(x}>0. 3°. Предел функции f(x) при неограниченном возрастании |х| равен нулю, т. е. ось ОХ является горизонтальной асимптотой графика функции  4°. Функция f{x) имеет в точке х = a  максимум, равный 5°. График функции f(x) симметричен относительно прямой х = а.6°. Нормальная кривая в точках х = а +  имеет перегиб,

  На основании доказанных свойств построим график плотности нормального распределения f(x).

 

 

 

  Как видно из рисунка, нормальная кривая имеет колоколообразную форму. Эта форма является отличительной чертой нормального распределения. Иногда нормальную кривую называют кривой Гаусса. При изменении параметра а форма нормальной кривой не изменяется. В этом случае, если математическое ожидание (параметр а) уменьшилось или увеличилось, график нормальной кривой сдвигается влево или вправо .

При изменении параметра  s изменяется форма нормальной кривой. Если этот параметр увеличивается, то максимальное значение  функции f(x) убывает, и наоборот. Так как площадь, ограниченная кривой распределения и осью Ох, должна быть постоянной и равной 1, то с увеличением параметра  кривая приближается к оси Ох и растягивается вдоль нее, а с уменьшением   кривая стягивается к прямой х=а .

Использование формул  f(x) и F(x) для практических расчетов затруднительно. Но решение задач по этим  формулам  можно упростить, если от нормального распределения с произвольными параметрами а и перейти  к нормальному распределению с параметрами а=0,  = 1. Функция плотности нормального распределения f(x) с параметрами а=0,   =1 называется плотностью стандартной нормальной случайной величины и ее график имеет вид:

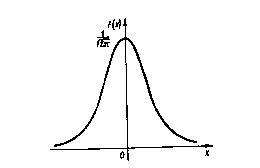Функция плотности и интегральная функция стандартной нормальной СВ будут иметь вид:

Для вычисления вероятности попадания СВ в интервал (a, b) воспользуемся функцией    Лапласа: Перейдем к стандартной нормальной случайной величине   Тогда

Значения функции Ф(u) необходимо взять из таблицы приложений "Таблица значений функции Ф(х)" .

21. Равномерное распределение прямоугольное распределение, специальный вид распределения вероятностей случайной величины Х, принимающей значения из интервала (а — h, a + h); характеризуется плотностью вероятности:

        

         Математическое ожидание:  Ех = a, дисперсия Dx = h²/3, характеристическая функция: С помощью линейного преобразования интервал (а — h, a + h) может быть переведён в любой заданный интервал. Так, величина Y = (X — a + h)/2h равномерно распределена на интервале (0, 1). Если Y₁, Y₂, ..., Y_n равномерно распределены на интервале (0, 1), то закон распределения их суммы, нормированной математическим ожиданием n/2 и дисперсией n/12, при возрастании n быстро приближается к нормальному распределению (даже при n = 3 приближение часто бывает достаточным для практики).

22.Нормальное распределение вероятностей Гаусса, дифференциальная функция распределения, вероятностный смысл параметров, нормированное нормальное распределение, интегральная функция распределения, функция Лапласа.

Нормальным называется распределение вероятностей непрерывной случайной величины,которое описывается плотностью . Мы видим,что нормальное распределение определяется двумя параметрами : а и … .Достаточно знать эти парамеры,чтобы задать нормальное распределение.Вероятностный смысл таков : а есть мат ожидание , … -среднее квадратическое отклонение нормального распределения. а) Математическое ожидание нормального распределения равно параметру а.б)Среднее квадратическое отклонение нормального распределения равно параметру σОбщим называют нормальное распределение с произвольными параметрами а и σ (σ>0). Нормированным называют нормальное распределение с параметрами а=0 и σ=1. Плотность нормированного распределенияϕ(х)=