1.Средние величины(гармоническое, геометрическое, арифметическое, квадратичное); примеры их применения; неравенства между средними; взвешенные средние.Средняя величина - обобщающая характеристика изучаемого признака в совокупности. Она отражает его типичный уровень в расчете на единицу совокупности в конкретных условиях места и времени.Средним гармоническим нескольких положительных чисел называется число, обратное среднему арифметическому их обратных, т. е. число Средним геометрическим нескольких положительных вещественных чисел называется такое число, которым можно заменить каждое из этих чисел так, чтобы их произведение не изменилось.

Среднее геометрическое взвешенное набора вещественных чисел Х1……Хn с вещественными весами W1…..Wn определяется так

В том случае, если все веса равны между собой, среднее геометрическое взвешенное равно среднему геометрическому.В математике и статистике сре́днее арифмети́ческое (или просто среднее) набора чисел — это сумма всех чисел в этом наборе, делённая на их количество.Среднее арифметическое является наиболее общим и самым распространённым понятием средней величины. Термин "среднее арифметическое" предпочитают в математике и статистике, чтобы отличать его от других средних величин, таких как медиана и мода. Частными случаями среднего арифметического являются генеральное среднее (генеральной совокупности) и выборочное среднее (выборки).Среднее квадратическое (квадратичное) — число s, равное квадратному корню из среднего арифметического квадратов данных неотрицательных чисел a1,a2,...,an:

Среднее квадратическое — частный случай среднего степенного и потому подчиняется неравенству о средних. В частности, для любых чисел оно не меньше среднего арифметического:

Среднее квадратическое находит широкое применение во многих науках. В частности, через него определяется основное понятие теории вероятностей и математической статистики — дисперсии (среднеквадратическое отклонение). Также тесно связан с этим понятием метод наименьших квадратов, имеющий общенаучное значение.

Средние величины применяются для оценки достигнутого изучаемого показателя, при анализе и планировании производственно-хозяйственной деятельности предприятий, фирм, банков.

Неравенства между средними

2.Элементы комбинаторики: перестановки, размещения, сочетания; формулы для вычесления;примеры.ПерестановкаПерестановки без повторений — комбинаторные соединения, которые могут отличаться друг от друга лишь порядком входящих в них элементов. Перестановкой из n элементов называется всякий способ нумерации этих элементовТеорема 1. Число всех различных перестановок из n элементов равно n!

Число всех перестановок обозначается PnРазмещения.Размещения без повторений — комбинаторные соединения, составленные из n элементов по m. При этом два соединения считаются различными, если они либо отличаются друг от друга хотя бы одним элементом, либо состоят из одних и тех же элементов, но расположенных в разном порядке.

Сочетания — комбинаторные соединения из n элементов по m, составленные из этих элементов и отличающиеся друг от друга только составом.

3.Бином Ньютона. Свойства биномиальных коэффициентов. Примеры:….Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид

, где - биномиальные коэффициенты.В математике биномиальные коэффициенты — это коэффициенты в разложении бинома Ньютона (1 + x)n по степеням x. Коэффициент при xk обозначается (иногда )

В комбинаторике биномиальный коэффициент интерпретируется как число сочетаний из n по k, равное количеству всех подмножеств (выборок) размера k в n-элементном множестве.Биномиальные коэффициенты часто возникают в задачах комбинаторики и теории вероятностей.Обобщением биномиальных коэффициентов являются мультиномиальные коэффициенты.Биномиальные коэффициенты обладают множеством различных свойств:-правило симметрии-внесение-вынесение-суммирование по K-суммирование по N-суммирование квадратов-взвешенное суммирование

4. Классическое, статистическое и математическое определение вероятности.

Классическое определение вероятностиВероятностью события А при проведении некоторого испытания называют отношение числа исходов, в результате которых наступает событие А, к общему числу всех равновозможных между собой исходов этого испытания.Классическим подходом к вероятности удобно пользоваться, когда количество всех равновозможных исходов в опыте ограничено и не слишком велико. Однако эти условия не всегда соблюдаются на практике: иногда приходится решать задачи, в которых число исходов постоянно меняется или бесконечно велико. Кроме того, не всегда события могут быть равновероятными.Практика показывает, что массовые случайные явления обладают одним уникальным свойством: с увеличением числа испытаний повышается устойчивость их появления. Например, если повторить опыт бросания монетки 100 раз, то примерно в 50% испытаний выпадет "орел", а в 50% - "решка". Если увеличить число испытаний до 1000 раз, это в конце концов приведет к еще большей устойчивости частоты полученных значений, а это уже определенная закономерность.При статистическом подходе нас интересует не исход отдельно взятого испытания, а то, что получается в результате его многократного повторения, то есть в качестве статистической вероятности события принимают частоту появления того или иного события при неограниченном увеличении числа испытаний.

Например, если в результате достаточно большого числа испытаний оказалось, что относительная частота весьма близка к 0.4, то это число можно принять за статистическую вероятность события.

5. Достоверное, невозможное, противоположное события; совместные, несовместные, зависимые независимые события, сумма и произведение событий. Примеры.

Достове́рным собы́тием в теории вероятности называется событие , которое в результате опыта или наблюдения непременно должно произойти.Для достоверного события P(U) = 1То есть вероятность события U равна единице.Невозмо́жным собы́тием в теории вероятностей называется событие, которое не может произойти в результате эксперимента. То есть событие, не содержащее ни одного элементарного исхода (что соответствует «пустому множеству» Ø в пространстве элементарных исходов).Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначеночерез A, то другое принято обозначать совместное событие в теории вероятности - событие, представляющее собой одновременное возникновение двух или нескольких других событий.Случайные события называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. Два события называют зависимыми, если вероятность появления одного из них зависит от наступления или ненаступления другого события.

Два события называют независимыми, если вероятность одного из них не зависит от появления или непоявления другого. Если каждые два из нескольких событий независимы, их называют попарно независимыми.Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий.Суммой А + B двух событий A и B называют событие, состоящее в появлении события A или события B, или обоих этих событий.Сложное событие, состоящее в совместном появлении нескольких простых событий. Например, событие A·B·C состоит в совмещении событий A, B и C.

6.Теорема сложения вероятностей; условная вероятность; теорема умножения вероятностей.

Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: P(A1+A2) = P(A1)+P(A2).Вероятность появления хотя бы одного из двух совместных событий A или B равна сумме вероятностей этих событий без вероятности их совместного появления: P(A+B) = P(A)+P(B)-P(AB). События A и B могут быть как независимыми, так и зависимыми.Условной вероятностью P(A|B) называют вероятность случайного события B , вычисленную в предположении, что случайное событие A , являющееся особым условием осуществления или неосуществления события B уже наступило.

Теорема. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: P(AB)=P(A)P(A|B).Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий: P(A1A2... An)=P(A1)P(A2)...P(An).

7.Вероятность появления хотя бы одного из нескольких событий,вероятность появления только одного события.Вероятность - P появления хотя бы одного из событий A1, A2, ... , An, независимых в совокупности, равна разности между единицей и произведением вероятностей - q противоположных событий `A1, `A2,..., `An: P(A) = 1- q1 q2...qn.

8.Полная группа событий, формула полной вероятности; формулы Бейеса вероятности гипотез.

Пусть в результате испытания наступит одно из единственно возможных событий A1,A2,...,An. Группу единственно возможных событий A1,A2,...,An называют полной. Сумма вероятностей событий, образующих полную группу, равна единице: P(A1+A2+...+An) = 1.

Вероятность события A, которое может наступить лишь при условии появления одного из несовместных событий B1,B2, ..., Bn, равна сумме произведений вероятностей из этих событий на соответствующую условную вероятность события A: P(A) = P(B1)·P(B1|A)+P(B2)·P(B2|A)+... +P(Bn)·P(Bn|A).Пусть опыт проведен, в результате его появилось событие А. Найдем вероятность гипотез, при условии, что А произошло

P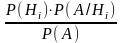 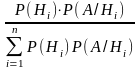(Hi|A) = =

9.Повторение испытаний, формула Бернулли.

Повторение испытаний. Пусть эксперимент повторяется n раз Используются незавивимые испытания (результаты каждого повторения не зависят от исходов предыдущих повторений)Событие А наступает в каждом испытании Р(А)=р. Найдём Рm,n, m- число испытаний, n – появление события АПусть в результате n независимых испытаний, проведенных в одинаковых условиях, событие А наступает с вероятностью Р(А) = р, а противоположное ему событие   с вероятностью Если в результате n опытов событие А наступает ровно т раз, то остальные n -т раз это событие не наступает Появление события А m раз в n испытаниях Вероятность каждой комбинацииПрименяя теорему умножения вероятностей несовместных событий:

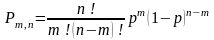- ---Формула Бернулли

10. Случайные величины, дискретные и непрерывные случайные величины.

. Случайной называют величину, которая в результате испытания примет с определенной вероятностью одно и только одно из возможных значений, наперед неизвестное и зависящее от причин, которые заранее не могут быть учтены. Переменную величину, значения которой жестко предопределены (детерминированы) вполне определенной причиной называют неслучайной переменной величиной. Дискретной (прерывной) случайной величиной называют случайную величину, которая может принимать отдельные, изолированные значения с определенными вероятностями. Непрерывной случайной величиной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.

11.Закон распределения дискретной случайной величины. Примеры.

Законом распределения дискретной случайной величины называют перечень всех возможных ее значений и их вероятностей. Обычно закон распределения задается в виде таблицы, одна графа которой содержит все возможные значения случайной величины, а вторая - соответствующие им вероятности: X : x1, x2 ,..., xn; P : p1, p2 ,..., pn. Представление закона распределения возможно также в виде формулы, посредством параметров или в виде графика.

12. Биномиальное распределение. Распределение Пуассона.Биномиальное распределение, распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях. Если при каждом испытании вероятность появления события равна р, причём 0 £ p £ 1, то число m появлений этого события при n независимых испытаниях есть случайная величина, принимающая значения m = 1, 2,.., n с вероятностями Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

13. Математическое ожидание дискретной случайной величины и его эмпирический смысл. Свойства матем. Ожидания:…….Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: M(X) = x1 p1+ x2 p2+...+ xn pn. Реально на основе данных выборки мы не можем вычислить M(X). Однако эту характеристику можно оценить. В качестве оценки можно использовать среднее арифметическое, то есть M(X) ≈`X. Чем больше объём выборки (число наблюдений), тем точнее эта оценка. Математическое ожидание обладает следующими свойствами: 1. Математическое ожидание постоянной величины равно самой постоянной: M(C) = C. 2. Постоянный множитель можно выносить за знак математического ожидания: M(CX) = CM(X). 3. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых: M(X+Y+Z) = M(X)+M(Y)+M(Z). 4. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий: M(XЧYЧZ) = M(X)ЧM(Y)ЧM(Z). Все эти свойства имеют большое практическое значение.

14.Мат.ожидание числа появления события А в одном и нескольких независимых испытаниях. Теорема. Математическое ожидание числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события испытаний: M(X)=np. Доказательство. Будем рассматривать в качестве случайной величины Х число независимых испытаний. Очевидно, общее число Х появлений события А в этих испытаниях складывается из чисел появлений события в отдельных испытаниях. Поэтому если Х₁-число появлений события в первом испытании, Х₂-во втором,…,Х_n-в n-м, то общее число появлений события Х=Х₁+Х₂+…+Х_n. По третьему свойству мат. ожидания, М(Х)=М(Х₁)+М(Х₂)+…+М(Х_n). Каждое из слагаемых правой части равенства есть мат. ожидание числа появлений события в одном испытании: М(Х₁)-в первом, М(Х₂)-во втором и т. д. Т. к. мат. ожидание числа появлений события в одном испытании равно вероят. события, то М(Х₁)= М(Х₂)= М(Х_n)= p. Подставляя в правую часть равенства вместо каждого слагаемого p, получим M(X)=np.

15.Дисперсия дискретной случайной величины формула для вычисления дисперсии. Свойства дисперсии: D(C), D(CX), D(X+Y), D(X-Y). Среднее квадратичное отклонение.Дисперсией случайной величины X называется математическое ожидание квадрата отклонений случайной величины от ее математического ожидания. Дисперсия обозначается как D(Х).Для дискретных случайных величин    т. е. дисперсия дискретной случайной величины равна сумме квадратов отклонений отдельных значений случайной величины от ее математического ожидания, умноженных на вероятности этих значений.Для непрерывных случайных величин  Положительный корень квадратный из дисперсии называется средним квадратическим (стандартным) отклонением случайной величины.

Эта величина обозначается, как .Дисперсия и стандартное отклонение характеризуют изменчивость (вариативность) случайной величины. Чем сильнее случайная величина отклоняется от своего математического ожидания, тем больше величины D(X) и . Последнюю ( ) использовать удобнее, так как его размерность совпадает с размерностью случайной величины (например, если Х - кол-во долларов, выигранное в лотерею, то - измеряется в $.

Свойства дисперсии 1. Дисперсия постоянной величины С равна нулю: D(C)=0.

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(CX)= C2D(X).3. Дисперсия суммы 2-х независимых случайных величин равна суме дисперсий этих величин: D(X+Y)= D(X)+D(Y),если X и Y – независимые с.в.4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: D(X-Y)= D(X)+D(Y)