Книги / Пискунов Н. С. Дифференциальное и интегральное исчисления. Том 1
.pdf

32
ПРЕДЕЛ
НЕПРЕРЫВJiОСТЬ
ФУНlЩИА
(ГЛ.
11
Докажем,
что
эта
nеременная величина имеет nредел, lхп-11=1(1+~)-1/=~.
равный
единице.
Имеем
Для где
любого 1/п < 8,
8 все
или п
nоследующие |
|
> 1/8, |
будут |
значения |
переменной, начиная с номера |
п, |
|
удовлетворять |
неравенству lхп-11 < 8, |
что |
|
и
требовалось
доказать,
Заметим,
что
здесь
nеременная
величина
стремится
к
пределу, П р и м
убывая. |
|
е р |
2. Переменная |
величина
х
последовательно
принимает
значения
Х1=1-
1 2
,
Х2=1+
1 22
;
Хз=l-
1 23
,
х,=1+
1 |
|
2 |
,, |
|
|
,
..
,
Хп=l+(-1)
11
1 |
|
2 |
п, |
|
|
Эта |
nеременная |
имеет предел, равный единице. |
Действительно, |
||||
|
|
|
1Хп-1.1 = 1(1 |
+(-l)nJ2n)- l l= 1J2n. |
|||
Д11я |
любого |
8, |
начиная с |
номера |
п, удовлетворяющего соотношению |
||
нз которого |
следует |
пJg 2 > lg (1/8), |
или |
п > lg)~, ), |
|||
|
|
|
2п > 1/8, |
||||
|
|
|
|
|
|
|
8 |
l/2n
<
8,
все
nоследующие
значения
х
будут
удовлетворять
соотношению
I
Хп-1
1<
8.
Оrметим,
что
здесь
значения
переменной
величины
то
больше,
то
меньше
nредела.
Переменная
величина
стремится
к
пределу,
«колеблясь
вокруг
него».
3
а
меч
ан
и
е
1.
Как
указывалось
в
§
3,
гл.
J,
постоянную
величину
с
часто
рассматривают
как
переменную
величину,
все
значения
которой
одинаковы:
х
=
с.
Очевидно,
что
предел
постоянной
будет
равен
самой
постоян
ной, |
|
так |
как |
всегда |
выполняется |
неравенство |
||
=0 |
< е |
при |
любом |
е. |
|
|
|
|
3 |
а меч ан и е 2. |
Из |
определения |
предела |
||||
Iх- с\= 1с -
следует, что
с1= пере
менная |
величина |
не |
может |
|
-нr |
''1.:))IS• |
|||
., |
1 |
|||
8 |
|
2, |
|
|
иметь
двух
пределов.
Действительно,
S<'!J./
если
~~- limx=a
и
limx=b
(а<Ь),
то
х
Р~.- должен
удовлетворять
сразу
двум
неравенствам
при
произвольно
lx-al малом в,
<е и
а это
lx-bl <в невозможно,
если
е
<
(Ь-а)/2
(рис. З
29). а меч
ан и
е
3.
Не
следует
думать,
что
каждая
переменная
величина
имеет
предел.
Пусть
переменная
величина
х
последова
тельно
принимает
следующие
значения:
X;t=
1 2
,
Ха=
1 1-·:р
1 Хв=s•
•
•
•t
Хм=
1-
1 22.t•
1 X211+t=~




§4)
БЕСI<ОНЕЧНО
МАЛЫЕ
И ИХ
ОСНОВНЫЕ
СВОЙСТВА
39
Теорем
а
2.
Если
lim
f
(х)
=
b=f=O,
то
функция
у=
1/f
(х)
|
|
|
|
|
|
|
х-+а |
при х - |
|
|
||
есть ограниченная функция |
а. |
|
||||||||||
|
До к аз ат ель ст в о. |
Из |
условия |
теоремы |
||||||||
произвольном |
8 > О |
в |
|
|
|
|
|
|||||
некоторой |
окрестности |
|
|
|
|
|
||||||
точки |
х=а будем |
иметь |
|
|
|
|
|
|||||
lf (x)-bl |
< 8, |
|
или |
|
|
|
|
|
||||
llf(x)I-IЬ11<8, |
или |
|
|
|
|
|
||||||
- |
< |
|
1- |
1Ь1 < 8, |
|
|
|
|
|
|||
8 |
1f (х) |
|
|
|
|
|
||||||
или |
\Ь\-8 |
< lf |
(х) |
1< |
|
|
|
|
|
|||
<1Ь1+8. |
|
|
|
нера- |
|
|
|
|
|
|||
|
Из |
пос..ледних |
|
|
|
|
|
|||||
следует,
что
при
венств
следует
1 Jb/-e
>
lf
1 (x)I
>
>
1 /Ьl+в
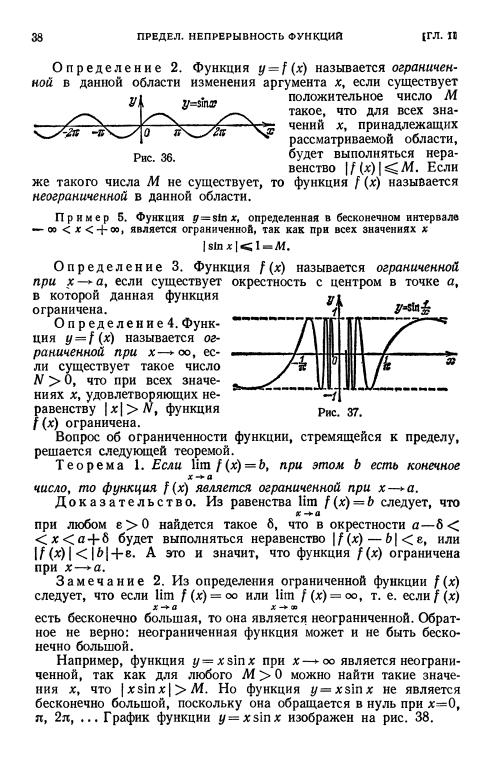
Рис.
38.
взяв,
например,
8
=
1 10
1Ь
\,
получаем
А
это
и
значит,
|
|
10 |
1 |
|
10 |
|
9 |
1Ь1> lf (х) 1 > -ТГТЪТ ' |
|||
что |
функция |
1/f |
(х) |
ограничена. |
|
§
4.
Бесконечно
малые
и
их
основные
свойства
В
этом
параграфе
будем
рассматривать
функции,
стремящиеся
к
нулю
при
некотором
характере
изменения
,аргумента.
О п р еде л е н и е.
.малой при х-а или
Функция а = а (х)
при х-+ оо, если lim
называется |
бесконечно |
et (х)=О или lima (х)=О. |
|
Из
определения
предеJJа
следует,
x
что
-J,,a если,
х--+rл например, lim
et
(х)=О,
то
это
значит,
что
для-любого
наперед
заданного
х-+а произвольно
малого
положительного8 найдется 6>0 такое, что для всех х, удовлетворяю
щих условию I х-а 1< 6, будет удовлетворяться условиеIа (х) \ < 8,
Пример |
1. |
Функция |
|
|
так как lim а= |
lim |
(х-1) |
2 |
|
х-+1 |
x • l |
|
|
|
Пр им ер |
2. |
Функция |
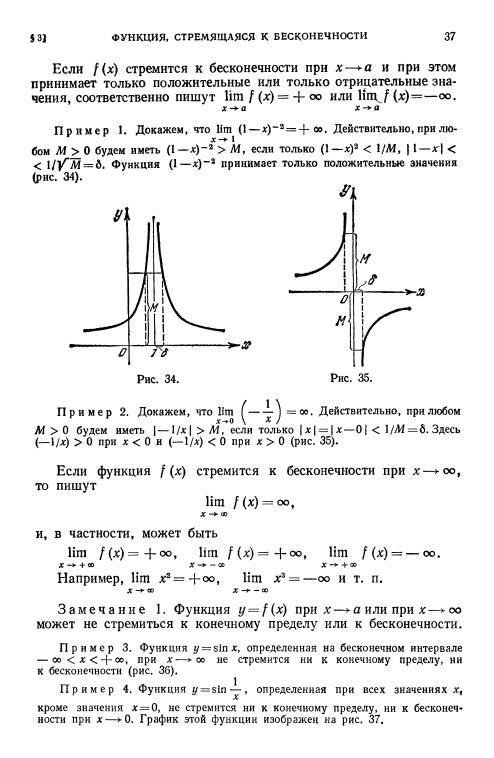
||
(рис. 40) (см. |
пример |
З § 2), |
||
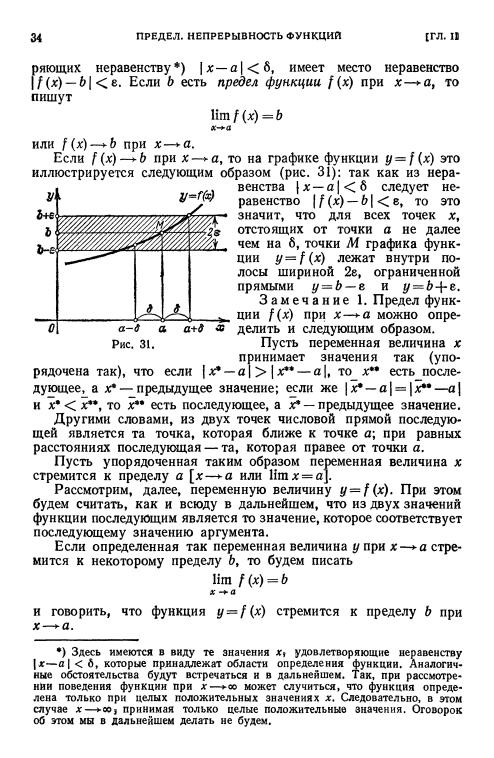
а=(х-1) |
2 |
есть бесконечно малая |
nри |
||
=0 (рис. |
39). |
|
|
||
а= 1/х |
|
есть |
бесконечно малая |
nри |
|
х->-1 |
1 |
|
|
х-+ оо |
|
Установим |
важное для |
дальнейшего |
соотношение: |
Теорема |
1. Если функция y=f |
(х) представляется |
|
суммы постоянного числа |
Ь и бесконечно малой а: |
||
в
виде
у=Ь+а:,
(1)