

ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования
«САНКТ-ПЕТЕРБУРГСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М. А. БОНЧ-БРУЕВИЧА»
Ю. Б. Фарфоровская, Е. Л. Рабкин
МАТЕМАТИКА
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ И БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
СПбГУТ)))
САНКТ-ПЕТЕРБУРГ
2013
УДК 51(077) ББК 22.1я73 Ф25
Рецензент заведующий кафедрой высшей математики СПбГЭТУ,
доктор физико-математических наук Н. А. Бодунов
Рекомендовано к печати редакционно-издательским советом СПбГУТ
Фарфоровская, Ю. Б.
Ф25 Математика. Дискретное преобразование Фурье и быстрое преобразование Фурье : методические указания / Ю. Б. Фарфоровская, Е. Л. Рабкин ; СПбГУТ. – СПб., 2013. – 32 с.
Написаны в соответствии с рабочим планом дисциплины «Математика».
Дискретное преобразование Фурье (ДПФ) – это преобразование временного сигнала (т. е. вектора отсчетов с равноотстоящими узлами) в частотную область. БПФ (быстрое преобразование Фурье) – алгоритм, позволяющий вычислять ДПФ достаточно быстро. Часто исследование ДПФ в частотной области позволяет увидеть и проанализировать особенности сигналов, которые более явно выражены в частотной области, чем во временной. С помощью ДПФ можно выделить (отфильтровать) полезный сигнал из смеси его с шумом. Огромное значение имеет возможность быстрого вычисления свертки двух временных последовательностей (в этом случае ДПФ этой свертки вычисляется как покоординатное произведение двух ДПФ от каждой из последовательностей). Это позволяет «быстро» решать очень важную «обратную» задачу, а именно быстро находить последовательность, круговая свертка которой с данной последовательностью дает требуемую последовательность.
Предназначены для студентов, обучающихся по специальностям
210700, 230400, 231000.
УДК 51(077) ББК 22.1я73
©Фарфоровская Ю. Б., Рабкин Е. Л., 2013
©Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «Санкт-Петербургский государственный университет телекоммуникаций им. проф. М. А. Бонч-Бруевича», 2013
2
|
СОДЕРЖАНИЕ |
|
ВВЕДЕНИЕ..................................................................................................................... |
4 |
|
1. |
ОПРЕДЕЛЕНИЕ ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ (ДПФ) И |
|
|
ЕГО ПРОСТЕЙШИЕ СВОЙСТВА.......................................................................... |
5 |
2. |
ЛИНЕЙНЫЕ И КРУГОВЫЕ СВЕРТКИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ. |
|
|
СВЯЗЬ ИХ С ДПФ..................................................................................................... |
12 |
|
2.1. Линейная свертка......................................................................................... |
12 |
|
2.2. Круговая свертка.......................................................................................... |
14 |
|
2.3. 4 свойства ДПФ, связанные с круговой сверткой.................................... |
15 |
|
2.4. Выражение линейной свертки через круговую........................................ |
17 |
3. |
БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ (БПФ).................................................... |
18 |
4. |
ДВА ПРИМЕРА ИСПОЛЬЗОВАНИЯ ДПФ И ИНДИВИДУАЛЬНЫЕ |
|
|
ЗАДАНИЯ К ЭТИМ ПРИМЕРАМ .......................................................................... |
22 |
|
Индивидуальные задания 1–20 .......................................................................... |
24 |
|
Индивидуальные задания 21–40 ........................................................................ |
27 |
СПИСОК ЛИТЕРАТУРЫ ............................................................................................. |
28 |
|
3
ВВЕДЕНИЕ
Дискретное преобразование Фурье (ДПФ) – это преобразование временного сигнала (т. е. вектора отсчетов с равноотстоящими узлами) в частотную область. Часто исследование ДПФ в частотной области позволяет увидеть и проанализировать особенности сигналов, которые более явно выражены в частотной области, чем во временной. Например, такое исследование позволяет идентифицировать голос отдельного человека и охарактеризовать числами особенности голоса отдельного человека, т. е. то, что мы выражаем словами «низкий голос», «высокий голос», «красивый голос» и т. д. Большое значение имеет также частотный анализ временного сигнала (т. е. анализ ДПФ этого сигнала), в частности, энергия спектральной плотности мощности этого сигнала (СПМ). Кроме того, ДПФ играет большую роль в «уплотнении» временного сигнала или, наоборот, в его «разнесении» по времени для различных целей. С помощью ДПФ также можно выделить (отфильтровать) полезный сигнал из смеси его с шумом.
ДПФ используется и для сжатия (компрессии) информации, передаваемой по каналам связи. Огромное значение имеет возможность быстрого вычисления свертки двух временных последовательностей. (В этом случае ДПФ этой свертки вычисляется как покоординатное произведение двух ДПФ от каждой из последовательностей). Это позволяет «быстро» решать очень важную «обратную» задачу, а именно, быстро находить последовательность, круговая свертка которой с данной последовательностью дает требуемую последовательность (то есть, грубо говоря, это означает, что можно быстро находить «переходную характеристику» предполагаемого устройства). Именно это мы рассматриваем как пример применения ДПФ в п. 4. Разумеется, мы не можем здесь коснуться всех многочисленных приложений ДПФ. Наша цель – дать математический аппарат основных понятий ДПФ, не касаясь огромного количества алгоритмов, связанных с реальными применениями ДПФ.
4

1. ОПРЕДЕЛЕНИЕ ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ (ДПФ) И ЕГО ПРОСТЕЙШИЕ СВОЙСТВА
Пусть имеется пространство последовательностей комплексных чисел длины п, которое будем обозначать Сn. Тогда элементы этого пространства
являются п-мерными векторами при этом вектор z = {z1, z2, …, zn} где zk – комплексные координаты вектора Z.
Естественным образом здесь определяются две линейные операции:
а) сложение векторов – при сложении векторов соответствующие координаты складываются, т. е. z + w = {z1 + w1, …, zn + wn};
б) умножение на комплексное число αz = {αz1, αz2,…, αzn}.
Эти две линейные операции обладают привычными свойствами линейных операций (можно их перечислить).
Более того, в Сп можно ввести скалярное произведение. Именно, если
n
z, w Cn , то (z, w) zk wk , где wk – комплексные числа, сопряженные с wk,
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т. е. если wk k ki, |
i |
1, |
то |
w |
k k ki. |
|
|
|
|
|||||
Напомним, что w |
w |
k |
| w |
|2 |
|
2 |
2 |
, |
|
k |
, |
k |
– вещественные числа |
|
k |
|
|
k |
|
|
k |
k |
|
|
|
|
|||
и что wk имеет тот же модуль, что и wk, а аргумент отличается знаком. Можно доказать следующие свойства скалярного произведения:
1)(z, w) (w, z) ; если z и w – вещественны, то (z, w) = (w, z);
2)(αz1+βz2, w) = α(z1, w) + β(z2, w); (z, w1 w2 ) (z, w1) (z, w2 ) .
Следствие: постоянный множитель из 1-го множителя выносится сам,
аиз 2-го сомножителя – как сопряженное число.
n |
n |
|
0 . Длиной вектора z в Cn (аналогично ве- |
||
3) (z, z) zk zk | zk |2 |
|||||
k 1 |
r 1 |
|
|
|
|
|
|
|
|
|
n |
щественному случаю) называется число | z | |
| zk |2 . |
||||
|
|
|
|
|
k 1 |
|
|
n |
zk |2 |
|
|
Таким образом, | z | |
| |
(z, z) . Число |z| будем называть моду- |
|||
|
|
k 1 |
|
|
|
лем вектора, или его нормой. |
|
n |
|
||
|
|
|
|
|
|
Заметим, что (z, z) 0 |
и (z, z) 0 |
| zk |2 0 , откуда все zk = 0, т. е. z |
|||
k 1
–нулевой вектор: z = 0 = {0, 0, …, 0} – нулевой вектор.
4)Неравенство Коши-Буняковского: модуль скалярного произведения не превосходит произведения модулей сомножителей, т. е.
5
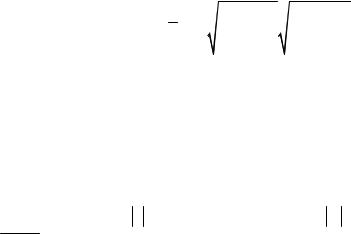
n |
n |
n |
|
||
| (z, w) | | zk |
w |
k | |
| zk |2 |
| wk |2 . |
(1.1) |
k 1 |
k 1 |
k 1 |
|
||
Доказательство. Пусть α – вещественное число. Рассмотрим скалярное произведение вектора z + αw самого на себя:
A(α) = (z + αw, z + αw) = (z, z) + (αw, z) + (z, αw) + (αw, αw).
Так как α вещественно, его можно выносить из любого сомножителя. Поэтому
A( ) z 2 (w, z) (z, w) 2 w 2 . Но (w, z) (z, w) и (w, z) (z, w) 2 Re(z, w).
Значит, A(α) = |z|2 + 2α Re(z, w) + α2|w|2 ≥ 0. Так как квадратный трехчлен А(α) ≥ 0 при всех α, то его дискриминант ≤ 0, и поэтому [Re(z, w)]2 –
|z|2|w|2 ≤ 0,
|z|2|w|2 ≥ [ Re(z, w)]2 |
или |
|Re(z, w)| ≤ |z| · |w|. |
(1.2) |
Из (2) следует (1). Пусть |
arg(z, |
w) = φ. Тогда вместо |
z возьмем |
z1 = z·e–iφ, а так как φ – вещественно, |z1| = |z|, и если r = |
|(z, w)|, то |
||
(z, w) = r·eiφ, откуда |
|
|
|
Re(z1, w) = Re(ze–iφ, w)) = Re(e–iφ(z, w)) = Re(e–iφ reiφ) = Re(r) = r = |(z, w)|.
Получаем из (1.2):
|z||w|=|z1||w| ≥ |Re(z1, w)|=|(z, w)|,
и неравенство (1.1) доказано.
Два вектора в Сп называются ортогональными, если их скалярное произведение равно 0:
z w (z, w) 0 .
Базисом в Сп называется набор из п векторов, через которые можно выразить все остальные векторы, т. е. таких векторов, что любой другой вектор пространства является линейной комбинацией базисных векторов (векторы базиса обязательно линейно независимы). Коэффициенты этой линейной комбинации и называются координатами этого вектора в данном базисе. Базис – максимальный (по числу элементов) набор линейно независимых векторов. Базис называется ортогональным, если любые 2 вектора базиса ортогональны между собой (в этом случае линейная независимость базисных векторов выполняется автоматически). Базис называется ортонормальным (или декартовым), если он ортогонален и нормы всех его векторов равны 1. Число векторов в базисе равно п и это число п называется
6
размерностью пространства Сп. Стандартный базис в Сп – (скользящая единица):
е1 = {1, 0, …, 0},
е2 = {0, 1, …, 0},
………………
еn = {0, 0, …, 1}.
Заметим, что в пространстве последовательностей длины п элементы каждой последовательности являются соответствующими координатами в стандартном базисе.
Любой набор из п линейно независимых векторов пространства также образует базис. Если в пространстве есть 2 базиса: новый { e1 , e2 ,...,en } и
старый {е1, е2, …, еn}, то матрицей перехода от старого базиса к новому называется матрица п-го порядка, в столбцах которой стоят координаты новых базисных векторов в старом базисе. Если А – такая матрица, то обяза-
тельно detA ≠ 0, и следовательно, существует А–1 – матрица перехода от нового базиса к старому; поэтому в ее столбцах стоят координаты старых базисных векторов в новом базисе.
Если z = {z1, z2, …, zn} – координаты вектора z в старом базисе, а w – в новом, w = {w1, w2, …, wn}, то w = Az, z = A–1 w (в обоих равенствах и сле-
ва, и справа записаны столбцы).
Наряду со стандартным базисом (из скользящих единиц) рассмотрим новый базис (что он действительно базис, будет доказано позднее):
|
|
|
|
2 ij |
, e |
4 ij |
2 (n 1)ij |
|
|
|
|
Z |
j |
|
1, e |
n |
n ,...,e |
n |
|
, |
j 0, |
1, ..., n 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом,
Z0 = {1, 1,…,1},
|
|
|
|
2 i |
|
4 i |
, ..., e |
2 (n 1)i |
|
|||
Z |
|
|
1, e |
|
n , e |
|
n |
n |
|
, |
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 i |
, e |
8 i |
,...,e |
4 (n 1)i |
|
||
Z |
2 |
|
1, e |
n |
n |
n |
|
, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
…………………………………
|
|
|
2 i(n 1) |
|
|
4 i(n 1) |
|
|
2 (n 1)i(n 1) |
|
|
|
n |
|
n |
|
n |
|
|||
Zn 1 |
1, e |
|
, e |
|
, ..., e |
|
. |
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
Тогда матрица перехода F= fij in, j 1 от стандартного базиса к базису
{Z |
} имеет вид (где обозначено b e |
2 i |
|
|
|
|||
|
n ) |
|
|
|
||||
k |
|
|
|
|
|
|
|
|
|
1 |
1 |
1...... 1 |
|
|
|
||
|
|
b |
b2....... bn 1 |
|
||||
|
1 |
|
||||||
|
|
b2 b4....... b2(n 1) |
|
|||||
|
F 1 |
. |
||||||
|
.......................... |
|
|
|||||
|
|
|
n 1 |
|
2(n 1) |
|
(n 1)2 |
|
|
|
b |
b |
...b |
|
|||
|
1 |
|
|
|
|
|||
Очевидно, что эта матрица симметрична, т. е. fij = fji. Кроме того, все элементы этой матрицы являются корнями п-ой степени из единицы, поэтому число различных элементов этой матрицы равно п и все эти числа находятся в ее второй строчке (кроме того, сумма элементов каждой строчки (кроме первой) равна нулю, что следует из доказанной далее леммы).
Докажем теперь что векторы Zj образуют ортогональный базис. Это доказательство основано на достаточно очевидном утверждении, которое мы оформим в виде леммы (оно нам понадобится и в дальнейшем).
Лемма. Пусть n, j, s натуральные числа. Рассмотрим сумму
n 1 |
|
2 ik ( j s) |
L e |
|
n |
|
|
|
k 0 |
|
|
n 1 |
k ( j s) |
b |
n . |
k 0 |
|
Тогда, если j s 0 (или j s 0 по модулю |
п, т. е. |
j s pn , где р – |
|
целое число), то L = 0, а в случае j s 0(mod n) |
L n . |
|
|
Доказательство. Заметим, что L представляет собой геометрическую |
|||
|
2 i |
( j s) 1 тогда и |
|
прогрессию со знаменателем q b j s , поэтому |
q e |
n |
|
только тогда, когда j – s делится на п. Поэтому при j s 0 и значит, q 1, по формуле для суммы членов геометрической прогрессии получаем
|
|
n |
|
|
|
2 i( j s)n |
|
|
2 i( j s) |
L |
1 q |
|
1 e |
|
n |
|
1 e |
||
|
|
|
|
||||||
1 q |
|
1 q |
1 q |
||||||
|
|
|
|
||||||
При j = s(mod n) bj – s, очевидно,
1 1 0. 1 q
равно 1 при всех k, и поэтому
n 1
L 1 n .
k 0
Лемма доказана.
8

Следствие. Базис Zj, (j = 0, 1, 2, …, n – 1) ортогонален и длина каждого
его вектора равна n .
Действительно, вычислим скалярное произведение
n 1 |
2 ikj |
2 iks |
n 1 |
2 ik ( j s) |
Z j , Zs e n |
e n |
e |
n |
|
k 0 |
|
|
k 0 |
|
n 1
bk ( j s). k 0
По лемме при j ≠ s это скалярное произведение равно 0, и значит, базисные векторы попарно ортогональны. При j = s это скалярное произведе-
ние равно квадрату длины вектора Zj и, по лемме, равно п. Следствие доказано.
Отсюда следует, что этот базис можно сделать ортонормальным (разделив все координаты каждого вектора на n ). Такая процедура часто осуществляется в математических исследованиях, но в многочисленных приложениях ДПФ обычно этого не делают.
Докажем, что обратной матрицей к F является матрица F*, состоящая из комплексносопряженныхэлементовматрицыF, поделенныхнап, т. е.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
1...... |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
b |
|
|
.......b 2 |
|
|
|
|
b n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
|
2(n 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
F* |
n |
1 |
|
b |
|
|
b |
|
|
....... |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.......................... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
2(n 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
b |
...b |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
k |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
напомним, что |
|
bk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рассмотрим произведение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
1 1 1...... |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 1 1...... |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
b b2 |
|
|
|
|
bn 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
n 1 |
|
|
|||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
b |
|
|
|
b |
|
|
|
|
|
b |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
F F* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2(n 1) |
|
|
|
|
|
|
|
|
|
2 b 4 |
|
|
|
|
b 2(n 1) |
|
|||||||||||||||||||||||||||||||
1 b2 b4 |
....... |
|
|
|
|
|
|
1 b |
|
....... |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
n |
.......................... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.......................... |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
n 1 |
|
|
2(n 1) |
|
|
|
n 1 2 |
|
|
|
|
|
|
n 1 |
|
|
|
|
|
2(n 1) |
|
|
|
|
|
n 1 2 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
b |
b |
...b |
|
|
b |
|
b |
...b |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
z |
0 |
, z |
0 |
z |
0 |
, z |
z |
0 |
, |
z |
2 |
...... |
|
|
|
|
|
z |
0 |
, |
|
z |
n 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
|
z1, z0 |
|
z1, z1 z1, |
|
z2 ...... |
|
|
|
|
|
z1, zn 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||
|
|
|
......................................................... |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
z |
n 1 |
, |
z |
0 |
z |
n 1 |
, |
z |
z |
n 1 |
, z |
2 |
..... |
|
|
z |
n 1 |
, z |
n 1 |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
В силу ортогональности все недиагональные элементы этой матрицы равны нулю, а на главной диагонали стоит число п, поэтому
9
|
|
n 0 |
0 ... 0 |
|
|
|||
|
|
|
0 |
n 0 ... 0 |
|
|
||
|
1 |
|
|
|
||||
F F* |
|
0 |
0 |
n ... 0 |
|
E , |
||
|
||||||||
n |
|
|||||||
|
|
................ |
|
|
||||
|
|
|
0 |
0 |
0 ... n |
|
|
|
|
|
|
|
|
||||
где Е – единичная матрица. Это и значит, что матрица F* является обратной к матрице F.
Замечание. Напомним, что матрицей, сопряженной к матрице А, называется матрица A* для которой при любых элементах х и у справедливо ра-
венство (Ах, у) = (х, A*y). Легко доказать, что элементы a*ij сопряженной матрицы задаются формулой a*ij = a ji . Так как F симметрична, а матрица
nF* состоит из элементов, комплексно сопряженных к элементам матрицы F, то матрица nF* и является сопряженной к матрице F, и значит, для всех х и у справедливо равенство (Fx, y) = n(x, F*y).
Заметим, что F* равна 1n , умноженной на матрицу, у которой в показа-
телях степеней экспонент нет минусов. Кроме того, все элементы этой матрицы, как и у матрицы F, являются корнями п-ой степени из единицы, поэтому число различных элементов этой матрицы равно п. Теперь мы можем дать определения прямого и обратного преобразования Фурье.
Определение. Прямым дискретным преобразованием Фурье (ДПФ) вектора z = (z0, z1, z2, …, zn – 1) в п-мерном пространстве называется новый
вектор w = (w0, w1, w2,…,wn – 1) этого пространства, определяемый формулой w = Fz, т. е.
w0 |
|
1 |
1 |
1...... 1 |
|
|
|
z0 |
|
z |
|
z |
z |
|
...z |
n 1 |
|
|
|
|
|
|
|||||||||
|
|
|
b2....... bn 1 |
|
|
0 |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1 |
b |
|
|
|
|
|
z |
0 |
bz |
b2 z |
2 |
... bn 1z |
|
|
|
|
||||||||||||
w1 |
|
1 |
|
|
|
|
|
|
|
|
z1 |
|
z |
|
1 |
|
|
|
|
|
|
|
|
n 1 |
|
. |
|||||
w |
|
b2 |
b4....... b2(n 1) |
z |
2 |
|
0 |
b2 z |
|
b4 z |
2 |
... b2(n 1) z |
n 1 |
||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
... |
.......................... |
|
|
... |
.......................................... |
|
|
|
|||||||||||||||||||||||
w |
|
|
|
|
|
|
|
|
(n 1)2 |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n 1)2 |
|
|
|
b |
n 1 |
b |
2(n 1) |
...b |
|
n 1 |
|
|
b |
n 1 |
z2 |
b |
2(n 1) |
z2 |
... |
b |
|
|||||||||||||
|
n 1 |
|
1 |
|
|
|
|
|
|
|
z0 |
|
|
|
|
|
zn 1 |
||||||||||||||
Таким образом, координаты вектора прямого преобразования Фурье определяются формулой
n 1 |
n 1 |
|
2 ikj |
|
|
wj bkj zk e |
|
n zk , |
j 0, 1, 2,..., n 1. |
(1.3) |
|
k 0 |
k 0 |
|
|
|
|
Это и есть общепринятые формулы прямого дискретного преобразования Фурье (прямого ДПФ). Вектор w = (w0, w1, …, wn) называют дискрет-
10

ным спектром вектора z = (z0, z1, …, zn). На практике очень удобно и часто применяется обозначение дискретного спектра w = zˆ .
Далее, из (3) получаем: z = F–1w = F*w. Так как F* отличается от F множителем 1n и знаков «минус» у экспонент нет, то верны формулы
|
1 |
n 1 |
2 ikj |
|
|
z j |
e |
n wk , |
j 0, 1, 2,..., n 1. |
(1.4) |
|
|
n |
|
|
|
|
|
|
k 0 |
|
|
|
Это и есть формулы обратного дискретного преобразования Фурье (обратного ДПФ).
Приведем, для примера, конкретные матрицы F4, F4*, F8.
1
11
1 F8 1
11
1
|
1 |
1 |
1 |
1 |
|
|
|
|
|
i |
1 |
i |
|
|
|
F 1 |
|
, F |
* |
||||
4 |
|
1 |
1 |
1 |
|
4 |
|
|
1 |
|
|
|
|||
|
1 |
i |
1 |
i |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
1 |
|
||||
1 |
|
(1 |
i) |
i |
1 |
|
( 1 i) |
||||||||||||
2 |
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
i |
|
1 |
|
|
|
|
|
i |
|
||||||
|
1 |
( 1 i) |
i |
1 |
|
(1 i) |
|||||||||||||
|
|
|
|
2 |
|
||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
1 |
|
|
|
1 |
|
||||||||
|
|
|
|
1 |
( 1 i) i |
|
1 |
|
|
(1 |
i) |
||||||||
|
|
|
|
2 |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
i |
|
1 |
|
|
|
|
i |
|
|||||
|
|
|
|
1 |
|
|
(1 i) |
i |
1 |
|
( 1 i) |
||||||||
|
|
|
|
2 |
|
|
|
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
1 |
1 |
1 |
|
|
1 |
|
i 1 |
i |
|
|
|
1 |
|
F 1 |
||||
4 |
|
1 |
1 |
1 |
|
4 |
1 |
|
|
||||
|
1 |
i |
1 |
i |
|
|
1 |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
1 |
|
|
( 1 i) |
i |
|
|
|
(1 i) |
|
||||||||||||
2 |
|
|
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
|
|
|
i |
1 |
|
|
|
|
|
i |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
(1 i) |
i |
1 |
|
|
( 1 i) |
|
||||||||||
|
|
|
|
|
|||||||||||||||||
2 |
|
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||
1 |
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
||||||
1 |
|
|
|
|
(1 i) |
i |
|
( 1 |
i) |
||||||||||||
|
|
|
|
|
2 |
|
|
|
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
i |
1 |
|
|
|
|
|
i |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
1 |
|
|
|
|
|
|
( 1 i) i |
|
|
|
|
(1 i) |
|||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
Замечание. Пусть заданная на всей оси функция f(x) такова, что для всех х вне отрезка [0, 1] все ее значения равны 0: для x [0, 1] f (x) 0 .
Тогда ее обычное преобразование Фурье задается равенством
fˆ ( ) |
1 |
f (t)e i t dt f (t)e i t dt. |
|
|
0 |
Интегральная сумма для последнего интеграла при разбиении отрезка [0, 1] на п равных частей (или, что то же, приближенное значение этого ин-
11

теграла по формуле прямоугольников) имеет вид |
fˆ ( ) |
1 |
n |
k |
|
|
2 ik |
||
f |
|
e |
|
n . |
|||||
|
|
|
|
n k 1 |
n |
|
|
||
Для j j эта формула принимает вид fˆ ( j) |
1 |
n |
k |
|
2 ikj |
Справа |
|||
|
f |
e |
n |
. |
|||||
|
n k 1 |
n |
|
|
|
|
|
|
|
стоит значение ДПФ для вектора z = (z0, z1, z2, …, zn – 1), где zk |
f k |
. Та- |
|||||||
|
|
|
|
|
|
|
n |
|
|
ким образом, ДПФ можно рассматривать как приближенное преобразование Фурье. Конечно, реальный сигнал не обязательно сосредоточен на отрезке [0, 1], но любой отрезок может быть преобразован в этот отрезок за счет линейного преобразования временной оси. Заметим также, что так как ДПФ вектора с одинаковыми координатами а равно вектору, у которого только первая координата равна па, а остальные координаты равны нулю, то «сдвиг» по оси y меняет у ДПФ только нулевую координату. «Сдвиг» сигнала по временной оси (с соответствующим изменением интервала) вообще ничего не меняет.
2. ЛИНЕЙНЫЕ И КРУГОВЫЕ СВЕРТКИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ.
СВЯЗЬ ИХ С ДПФ 2.1. Линейная свертка
Важным свойством любого линейного преобразования является действие этого преобразования на линейную свертку. Поясним это более подробно. Пусть имеется линейное (техническое) устройство, которое схематически выглядит так:
вход |
|
выход |
y |
|
z = Ly |
|
|
|
Здесь у – входной сигнал, а z = Ly – выходной. Линейность этой системы означает, что преобразование входного сигнала является линейным, т. е.
L(y1 + y2) = Ly1 + Ly2 и L(cy) = cLy.
Иными словами, линейным комбинациям входных сигналов соответствуют линейные комбинации с теми же коэффициентами выходных сигналов. Естественно, мы считаем, что любой входной сигнал – это элемент линейного пространства, т. е. вектор или функция. Например, линейными устройствами являются линейные электрические цепи или разного рода
12
фильтры (т. е. устройства, умеющие распознать и разделить разного рода входные сигналы, в частности, устранять определенного рода помехи).
Предположим, что на вход такой линейной системы подается единичный по величине достаточно короткий импульс. На выходе на этот сигнал последует определенная реакция (которая считается всегда одинаковой). Часто эта реакция оказывается гораздо длиннее по времени поданного импульса. Приближенно эту реакцию представляют в виде конечной последовательности
чисел (коэффициентов) zk, k = 0, 1, 2, …, n – 1, причем каждое число рассматривается как реакция системы за единичный по времени такт, который имеет некоторый номер k. Эта последовательность называется переходной характеристикой данного устройства. Если же на вход подается конечная последовательность (единичных по времени) сигналов с коэффициентами
{yk}, k = 0, 1, 2,…, m – 1, то на выходе должна получиться линейная свертка
последовательностей {yk} и {zk}. Действительно, обозначим начало реакции нашего устройства нулевым тактом (единичным по продолжительно-
сти), а ее величину в k-ом такте символом {wk}. Тогда очевидно, что
w0 = y0z0,
w1 = y0z1 + y1z0,
w2 = y0z2 + y1z1 + y2z0,
…………………………
wn–1 = y0zn-1 + y1zn-2 + …+yn-1z0,
wn = y1zn-1 + y2zn–2 +y3zn-3 +… + ynz0.
…………………………………………
wm + n-2 = ym – 1zn–1.
Предполагается, что последовательность {yk} продолжена нулями, когда т < п. Таким образом, реакция на сигнал из т тактов содержит ровно т + п – 1 такт.
Последовательность {wk} и называется линейной сверткой последова-
тельностей {yk} и {zk}. Заметим, что если обе последовательности продолжить нулями, то координату свертки с номером r можно записать в виде
|
|
|
wr ys zr s , |
r 0, 1, 2, , m n – 2. |
(2.1) |
s 0
Таким образом, линейная свертка двух последовательностей {yk} и {zk} – это новая последовательность {wk}, обозначаемая символом
w = y z = {wr}.
13
