Коррекционный и регрессионный анализ

1. Общее понятие о коррекционном и регрессионном.

2. Основные показатели парной корреляции и их оценивание по выборочным данным.

3. Формализация корреляционной связи путем построения уравнения регрессии

4. Понятие множественной корреляции. Множественный регрессионный анализ

Коррекционный и регрессионный анализ - смежные разделы статистики и теории вероятностей предназначенной для выявления измерения силы и формализации статистических связей между теми или иными статистическими признаками.

Детерминированные связи – связи в которых одному значению факторного признака соответствует единственное значение результативного признака (наиболее часто это различные функции)

Стакастические (статистические) связи – связи в которых одному значению факторного признака соответствует целое распределение значения результативного признака.

Корреляционная связь – является частным случаем статистической связи, когда факторные и результирующий признак имеют количественное выражение

Если фактор один – говорят о парной корреляции

Если факторов много – говорят о множественной корреляции

Выявление наличия корреляционной связи, её измерение проводят путем решения следующих задач.

1. Построение корреляционного поля

2. Расчет выборочных корреляционных характеристик

3. Проверка значимости

Построение корреляционного поля

X – факторный признак

Y – результативный признак

Корреляционное поле – график отражающий характер совместного поведения значений факторного и результативного признака. График является точечным. Строится так чтобы график имел форму квадрата

В зависимости от характера расположения точек можно предположить

1. Наличие прямой корреляционной связи (точки на одной линии)

2. Отсутствие корреляционной связи (точки расположены хаотично)

3. Наличие нелинейной корреляционной связи (точки на ломаной линии)

4. Наличие обратной корреляционной связи (точки расположены *сверху вниз*)

Дальнейшее задачей является измерение силы связи для чего используют 3 показателя

1. Коэффициент ковариации

COV_XY = .

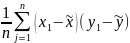Если связь линейная то ковариация положительная, если обратная линейная то отрицательная. Если ковариация = 0, то линейной связи нет.

Неудобство коэффициента в том, что он зависит от абсолютных значений принимаемых факторным и результативным признаком. в связи с этим вводят коэффициент линейной корреляции (нормированный коэффициент ковариации)

2. Коэффициент линейной корреляции (в случае предположения линейной связи)

ρ_XY=

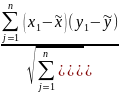
P=-1 – наличие строгой обратной функциональной связи

P=1- наличие прямой функциональной связи

В остальных случая ковариационная связь

Ковариация = 0 то и корреляция = 0 => отсутствие связи

3. Корреляционное отношение (в случае любой формы связей). Является универсальным показателем связи. Расчет этого показателя основан на применении правила сложения дисперсий

S²=Ϭ²+

S²=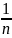

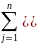
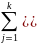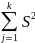Ϭ ²= f_i

= f_i

=

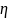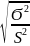
В связи с тем что коэфициент корреляции оценивается по выборочным данным, то он является случайной величиной и => может принять любое значение выборки (например значение 0,95 – связь сильная, а в генеральной совокупности этой связи нет) в связи с этим необходимо проверить статистическую гипотезу о значимости коэффициента корреляции.

Проверка данной гипотезы зависит от объема выборочных наблюдений

Z=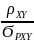

Ϭ_PXY – среднее квадратическое отклонение

Проверка значимости корреляционного отношения

H₀: _xy=0

H₁: _xy≠0

Нулевая гипотеза принимается если

F< _a(k-1,n-k)

Формализация корреляционных связей путем построения уравнения регрессии

Е сли наличие линейной корреляционной связи доказано, то следующим этапом является формализация связей – представление её в виде некоторого уравнения

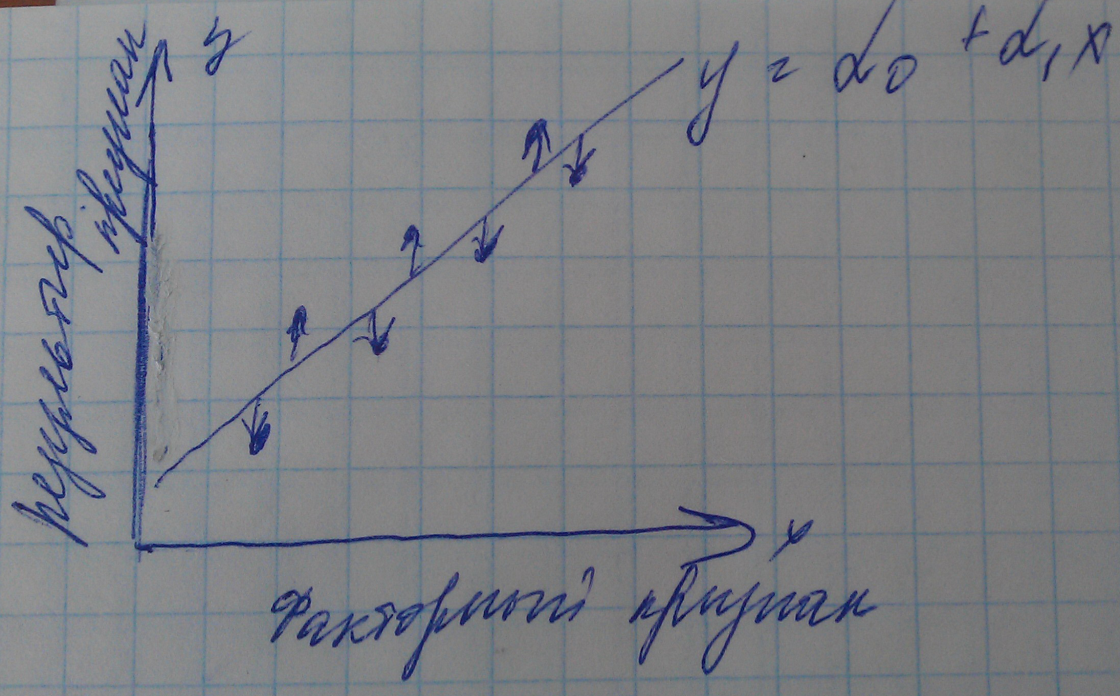
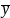=α₀+ α₁X

Коэффициенты α – коэффициенты регрессии

Задачей регрессионного анализа является – нахождение неизвестных коэффициентов уравнения регрессии по выборочным данным.

Основным методом определения неизвестных коэффициентов α₀ и α₁ является метод наименьших квадратов (МНК). Сущность метода заключается в минимизации суммы квадратов отклонений наблюдаемых значений результирующего признака У от значений рассчитываемых по уравнению регрессии.

Y^ - значение результата признака рассчитываемое по уровню регрессии Х

Y- значение результата признака полученное в результате наблюдений

F(α₀ α₁) =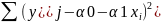 Для определения значения неизвестных коэффициентов α₀ и α₁ необходимо от функции F взять частные производные от α₀ и α₁ и приравнять к 0

СИСТЕМА УРАВНЕНИЙ

Полученная система уравнений называется системой нормальных уравнений метода наименьших квадратов

Из полученного соотношения следует что уравнение регрессии должно проходить через точку с координатами ( )

Пусть имеются данные по группе предприятий по производительности труда (результирующий признак) и величине фонда вооруженности.

Номер предприятия	Производительность (тыс. руб) У	Фондоотдача (тыс.руб.чел.) Х	xy	x*x	Y*Y
1	360	15,2	5472	231,04	129600
2	298	12,8	3814,4	163,84	88804
3	328	13,8	4526,4	190,44	107584
4	330	14	4620	196	108900
5	366	16,3	5965,8	265,69	133956
6	316	12,6	3981,6	158,76	99856
7	334	13,2	4408,8	174,24	111556
8	300	12,9	3870	166,41	90000
СУММА	2632	110,8	36659	1546,42	870256

Коэффициенты α₀ и α₁ полученные по данным регрессии являются случайными и могут принять ЛЮБЫЕ значения генеральной совокупности значений результирующего и факторного признака

Отсюда возникает задача проверки статистической значимости коэффициенты уравнения регрессии α₀ и α₁.

Порядок проверки

1. Определяется величина называемая остатком, для каждого наблюдения

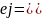
2. Определяется дисперсия остатка

Ϭ²=

3. Для коэффициентов α₀ и α₁ определяются их средние квадратические ошибки.

Ϭ_α0=Ϭ/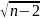 Ϭ_α1=Ϭ/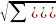

4. Для каждого коэффициента рассчитываются критерии Стьюдента

T_α0/1 = |α_0/1|/Ϭ_α0/1

5. Полученные значения сравниваются с критической границей распределения Стьюдента с n-2 степенями свободы при уровне значимости р.

Если выполняется условие t_α0>t_p(n-2) коэффициент α₀ признается статистически значимым.

Коэффициент α₀ признается не значимым то это не свидетельствует об отсутствии связи между факторным и результирующим признаком

Если коэффициенты регрессии оказались значимым то для них принято указывать доверительные интервалы с уровнем доверительной вероятности 1-р

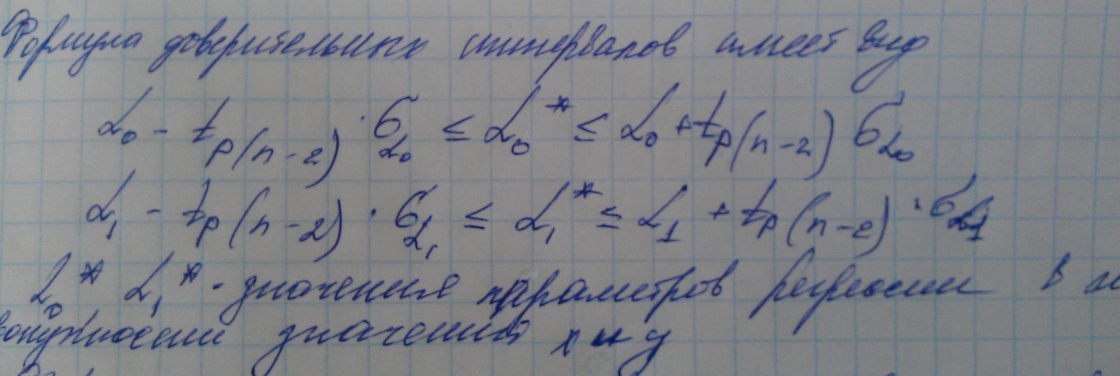
Формулы для расчета доверительных интервалов показывают что неизвестные значения параметров регрессии с вероятностью 1-р содержатся в указанных интервалах

После определения значимости и построения доверительных интервалов для параметров регрессии осуществляют оценку качества всего уравнения регрессии в целом. Такую оценку проводят с использованием коэффициента детерминации R²

R²= 1 -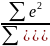

R²=

Точечная форма прогноза (прогноз в среднем) осуществляется подстановкой значения х* в уравнение регрессии

По полученому уравнению регресии принято также определять коэффициенты эластичности бета-коэфициент и дельта-коэфициент

Э=α₁* /

Данный коэффициент показывает на сколько % изменится

Β= α₁*Sx\Sy

Показывает на сколько % изменится значение среднего квадратического отклонения результирующего признака если среднее квадратическое отклонение факторного признака изменится на 1%

∆=ρ_XY*β/R²

Показывает какая доля вариации результирующего признака объясняется влиянием факторного признака