
- •По гСтатитика!!
- •Статистика как наука. Предметы и объект статистической науки. Основные категории.
- •Социально-экономическая статистика и статистика населения
- •Статистические показатели
- •Получаемы данные должны быть сопоставимы
- •Данные должны быть своевременны
- •Группировка и сводка результатов статистического наблюдения.
- •Абсолютные, относительные и средние статистические величины
- •Описательные статистики
- •Любой центральный момент порядка может быть выражен через -начальных моментов
- •Показатели вариации альтернативного признака
- •Выборочный метод в статистике
- •Проверка статистических гипотез
- •Анализы взаимосвязей социально-экономических явлений
- •Коррекционный и регрессионный анализ
- •Анализ множественной корреляции. Множественный регрессионный анализ
- •Сезонные колебания в рядах динамики. Моделирование сезонности
- •Индексный метод в статистике
- •По степени охвата элементов совокупности
- •По содержанию и характеру индексируемой величины
- •По методологии расчета
- •Индексы качественных показателей
- •Статистика доходов и расходов
- •Основные виды доходов и расходов населения
- •Статистика цен и статистика инфляции
- •Расчет ипц
- •V.Cтатистические показатели инфляции
Любой центральный момент порядка может быть выражен через -начальных моментов
ɱ2
=
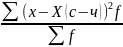 =
=
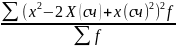 =
=
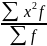 – 2х(сч)
+ х(сч)^2
– 2х(сч)
+ х(сч)^2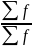 = m2
– 2m12+m12
= m2-m12
=
- (x(сч))^2
= m2
– 2m12+m12
= m2-m12
=
- (x(сч))^2
Кроме начальных и центральных моментов в некоторых случаях рассматривают условные моменты
Mβ
=

Асимметрия
As
=
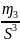
Если асимметрия + то основная масса частот находится правее средней арифметической, если – то левее средней арифметической.
При проведении статистических наблюдений асимметрия в рядах распределений может быть как случайной так и закономерной .
Для анализа случайностей или закономерностей асимметрии (несущественности или существенности) рассчитывают среднюю квадратическую ошибку асимметрии
ϬAS
=
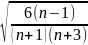
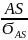 >
3
- существенна
>
3
- существенна
=< 3 – несущественная
Ex – эксцесс
Ex
=
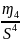 – 3
– 3
Показатель эксцесса рассчитывают с целью сравнения распределения статистической совокупности с теоретическим нормальным законом распределения случайных величин. (закон Гаусса)
Ex < 0 – распределение плосковершинное
Ex > 0 – распределение островершинное
Значение величины эксцесса также может быть обусловлено случайными и не случайными причинами
Для определения существенности или не существенности эксцесса рассчитывают среднеквадратическую ошибку эксцесса
ϬEx=
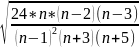
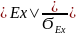 >
3 – существенный
>
3 – существенный
=< 3 – несущественный
Показатели вариации альтернативного признака
При измерении вариации альтернативного признака его значениям присваивают условно числовые значения 0 или 1
0 – отсутствие признака
1 – присутствие признака
В этом случае ряд распределения будет выглядеть так
Значение признака |
Частота повторений |
0 1 |
n-f f |
Итого |
n |
Х
(сч) =
=
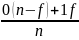 =
=
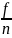 = -
= -
1 - = 1- p =q
S2=
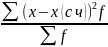 = p2q
+ q2p
= qp (p+q) = qp =
= p2q
+ q2p
= qp (p+q) = qp =
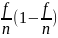
S
=
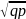
Правило сложения дисперсий
Если статистическая совокупность разбита на несколько групп и в каждой из групп известны индивидуальные значения признака, то в этом случае по каждой из групп могут быть определены групповые средние и групповые дисперсии
Xj(сч) – среднее арифметическое значение признака в j-й группе совокупностей
X(сч) – среднее значение признака по всей совокупности
S2j - дисперсия признака в j-й группе
S2 – общая дисперсия по все совокупности
∆2
=
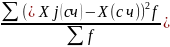 – дисперсия
групповых средних
– дисперсия
групповых средних
S2(сч)
=
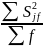
S2= ∆2 + S2(сч) – правило сложения дисперсий
Использование этого правила позволяет проанализировать какая доля вариаций исследуемого признака определяется вариацией значения признака положенного в основание группировки.
Данный анализ проводится на основе коэффициента детерминации
R2=
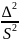
Выборочный метод в статистике
Основные понятия. Классификация выбора
Выборочные характеристики. Средние и предельные ошибки выборочного наблюдения
Средние предельные ошибки в выборках в условиях малых выборок
Доверительные интервалы для характеристики генеральной совокупности
Различные формы организации выборочного наблюдения
Сущностью выборочного метода является получение надежных и достоверных выводов об общих характеристиках изучаемого явления на основе наблюдений за ограниченной частью статистической совокупностью. При этом выводы о характеристиках явления должны содержать в себе указания на степень надежности получаемых результатов.
При использовании выборочного метода все результаты содержат указания на их достоверность с вероятностной точки зрения.
Выборка – часть статистической совокупности, отобранная из нее для получения данных о характеристиках всей совокупности в целом. В это случае всю статистическую совокупность называют генеральной совокупностью, а часть совокупности называют выборочной совокупностью.
Любая выборка должна обладать тремя основными свойствами
Репрезентативность – выборочная совокупность должна правильно представлять пропорции генеральной совокупности
Случайность – любой элемент генеральной совокупности должен иметь равную со всеми остальными вероятность быть отобранным в выборку.
Достаточность – объем выборочной совокупности должен обеспечить заранее заданную степень надежности получаемых выводов
Классификация выборок проводится
по форме отбора единиц
повторные
бесповторные выборки
по степени охвата единиц
большие
малые
по способу формирования
простые случайные
расслоенные
серийные
механические
комбинированные
ступенчатые
многофазные
Простые выборки. Выборочные характеристики. Средние предельные ошибки выборки
В условиях простой случайной выборки единицы наблюдения извлекаются из генеральной совокупности без её предварительного расчленения на какие-либо группы.
Отбор может быть
повторным – исследованная единица наблюдения возвращается в генеральную совокупность
без повторный – обследованная единица в генеральную совокупность не возвращается
Все характеристики получаемые по выборочным данным принято называть выборочными (эмпирическими) и считать оценками соответствующих характеристик генеральной совокупности.
В связи с различием выборочных характеристик и характеристик генеральной совокупности для них принято использовать различное обозначение, либо изначально оговаривать о какой характеристике идет речь
Проблемой использования выборочных характеристик как оценок характеристик генеральной совокупности заключается в том что все выборочные характеристики являются случайными величинами, что предопределяет наличие возможных расхождений между выборочными и генеральными характеристиками. Эти расхождения принято называть ошибками выборочного наблюдения (ошибки репрезентативности).
Пусть например для генеральной совокупности состоящей из трех семей требуется определить среднее количество детей в семье по выборке из двух семей.
Семьи |
1 2 3 |
Кол-во детей |
1 2 3 |
Номера семей в выборках
1.1 - 1
1.2 - 1.5
1.3 - 2
2.1 - 1.5
2.2 - 2
2.3 - 2.5
3.1 - 2
3.2 - 2.5
3.3 – 3
Любая выборочная характеристика является случайной величиной.
Это определяет наличие возможных или расхождений между характеристиками генеральной совокупности и характеристиками выборочной совокупности
То что математическое ожидание выборочной средней равно среднему значению в генеральной совокупности (данное свойство справедливо практически для всех выборочных характеристик предопределяет их использование
D(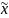 )
=
)
=
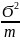
D(p)
=
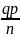
Средние квадратические отклонения выборочных характеристик принято называть средними ошибками выборки.
Для случая повторного отбора
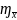 =
=
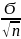
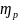 =
=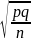
Для случая без повторного отбора
=
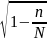
=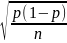 (1-
(1-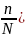
Наряду со средними ошибками выборки при проведении выборочных наблюдений принято вычислять предельную ошибку выборки
Предельная ошибка выборки – максимально допустимая по модулю отклонение выборочной характеристики от характеристики генеральной совокупности.
Одновременно с понятием предельной ошибки выборки, вводится понятие риска или уровня значимости.
Риск или уровень значимости – вероятность того, что выборочная характеристика отклонится от характеристики генеральной совокупности на величину большую предельной ошибки выборки.
P(|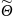 – Θ| > ∆) = α
– Θ| > ∆) = α
Θ – характеристика генеральной совокупности
- выборочная характеристика
∆ - предельная ошибка выборки
α – риск и уровень значимости
Вероятность противоположного события принято называть доверительной вероятностью или уровнем надежности.
P(| – Θ| =< ∆) = 1-α
Предположим
что,
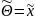 ,
Θ=
,
Θ=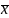
P(| – | =< ∆) = 1-α =
 =
1- α
=
1- α
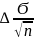 =
Uα
-
предположим
=
Uα
-
предположим
При выполнении определенных условий левая часть неравенства будет являться стандартной нормально распределенной случайно величиной.
 =
|Z|
=
|Z|
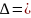 Uα
= Uα
*
(1)
Uα
= Uα
*
(1)
В итоге
P(|Z| =< Uα) = 1- α
ИЛИ
P(|Z|
=< Uα)
= 2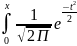 dt=
2Ф(Uα)
dt=
2Ф(Uα)
Функция Ф(….) является нормированной функцией Лапласа и её значения для разных значений функции является табулированным.
Следовательно
2 Ф(Uα)
= 1- α
Ф(Uα)
= 1- α
Ф(Uα)
=
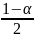 (2)
(2)
Сравнивая выражения 1 и 2 можно сделать выводы:
величина предельной ошибки выборки полностью определяется величиной средней ошибки выборки
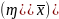 и значением коэффициента Uα
и значением коэффициента Uα
значение коэффициента Uα полностью определяется заранее назначенным уровнем доверительной вероятности
чем больше уровень доверительной вероятности (1-α), тем большим является значение Uα, причем если (1- α) -> 1 то Uα -> ∞. Отсюда следует что при проведении выборочных наблюдений невозможно обеспечить 100% достоверность определения характеристик генеральной совокупности. Эти характеристики могут быть определены с определенной долей вероятности от 0,9 до 0,99.
Полученные формулы и сделанные выводы позволяют записать последовательность определения предельных ошибок выборки в виде следующего алгоритма.
Задать уровень доверительной вероятности (1 – α) и с использованием формулы 2 по таблицам нормированной функции Лапласа определить значение коэффициента Uα
Определить среднюю ошибку выборки
Рассчитать предельную ошибку выборки
Окончательно получаем формулу для расчета предельной выборки
∆x
= Uα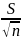 = Uα
*
Ф(Uα)
=
(3)
= Uα
*
Ф(Uα)
=
(3)
∆p
=
Uα
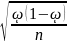 Ф(Uα)
=
(4)
Ф(Uα)
=
(4)
Рассмотрим следующий пример
Пусть при 100 подбрасываниях монетки было получено 55. Определить с вероятность 0,95 величину предельной ошибки выборки при определении генеральной вероятности выпадения одной решки в одном испытании.
F = 55 (количество решек)
N = 100 (общее количество бросков)
Следовательно
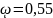
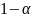 =
0,95 => Uα
=
1,95
=
0,95 => Uα
=
1,95
∆p
=
1,96
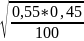 =
0,1
=
0,1
Формулы 3 и 4 получены для условий повторной выборки
Для условий без повторной выборки предельные ошибки вычисляются по формулам
∆x
= Uα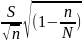 =
Uα
*
(5)
=
Uα
*
(5)
∆ p
=
Uα
p
=
Uα
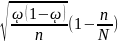 (6)
(6)
Формулами 3, 4 ,5 и 6 пользуются также для определения необходимого объема выборочных наблюдений обеспечивающего заранее заданный уровень надежности результатов и заранее заданную предельную ошибку. \
n
=
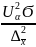
n
=
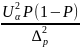
Формула для малых выборок
В условиях малых выборок для расчета предельной ошибки выборки для генеральной средней использую формулу (Стьюдента)
∆x
=
tα
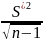
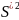 =
=
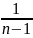
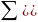 )2f
)2f
Значение величины tα определяется использованием распределением таблиц Стьюдента в зависимости от уровня значимости α и числа степеней свободы n-1
Значение величины tα определяется с использованием распределительных таблиц Стьюдента в зависимости от уровня значимости α и числа степеней свободы n-1
Доверительные интервалы для характеристик генеральной совокупности
Умение находить предельные ошибки выборки позволяет рассчитывать так называемые доверительные интервалы с уровнем доверительной вероятности 1-α для характеристик генеральной совокупности
P(| – Θ| =< ∆) = 1-α
P( – ∆ ≤ Θ ≤ + ∆) = 1-α – доверительный интервал]
Для повторного отбора больших выборок
P( – Uα ≤ ≤ + Uα ) = 1-α Uα
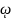 – Uα
≤ P
≤
+ Uα
– Uα
≤ P
≤
+ Uα
Для бесовторного отбора больших выборок
P(
– Uα ≤
≤
+ Uα
)
= 1-α
≤
≤
+ Uα
)
= 1-α
– Uα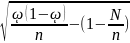 ≤ P
≤
+ Uα
-
≤ P
≤
+ Uα
- )
)
