Проверка статистических гипотез

Статистическая гипотеза – некоторое предположение о генеральной совокупности которая проверяется с использованием выборочных данных

Примеры статистических гипотез

1. в генеральной совокупности генеральное среднее значение = a₀

2. Генеральные средние в двух различных генеральных совокупностях равны между собой

= a₀

₁= a₀

3. Выборка х₁, х₂ и т.д. извлечена из генеральной совокупности которая подчиняется нормальному закону распределения случайных величин

4. Две выборки х_11, х_21, х_22, и т.д. извлечены из одной и той же генеральной совокупности

Все статистические гипотезы делятся на две группы

1. Параметрические. Если в статистической гипотезе содержится утверждение о числовых характеристиках (параметрах) генеральной совокупности то такие гипотезы называются параметрическими

1. Простые (1 параметр)

2. Сложные (2 и более параметров)

2. Непараметрические. Если в гипотезе содержится утверждение о генеральной совокупности в целом то они называются непараметрическими.

Правила записи статистических гипотез

Любую статистическую гипотезу принято формулировать в виде основной или нуль-гипотезы

H₀: содержание гипотезы

H₀: = a₀

На ряду с нулевой гипотезой формируется альтернативная гипотеза являющаяся логическим отрицанием нулевой гипотезы

H₁: ≠ a₀

Общие алгоритмы проверки статистических гипотез

1. Сформулировать основную или нуль-гипотезу

2. Сформулировать альтернативную гипотезу

3. По данным выборочного наблюдения рассчитать величину Θ которая называется статистикой гипотезы

4. Установить закон распределения статистики Θ

5. Область возможных значений статистики разбить на две взаимодополняющие подобласти:

первая – область принятия статистической гипотезы

вторая – область отвержения статистической гипотезы

Если статистика Θ попадает в область принятие гипотезы – гипотеза не отвергается, в противном случае отвергается в альтернативной

Разбиение области значения статистики производится по определенным правилам и определяется назначенным уровнем значимости проверки статистической гипотезы

При проверки уровень значимости – α, а область значения статистики разбивается таким образом чтобы выполнялось условие P(Θ> Θ_α) = α

Θ_α принято называть критической границей при проверки статистической гипотезы

Гипотезы о параметрах генеральных совокупностей

Н₀: = a₀

Среднее квадратическое отклонение в генеральной совокупности является известным.

Статистикой для проверки гипотезы является величина

Z=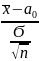

Критические границы при проверке такой гипотезы устанавливаются в зависимости от вида альтернативной гипотезы

Н₁: < a₀ Принимается при | Z|< -U_2α

Н₂: > a₀ Принимается при | Z|< U_2α

Н₃: ≠ a₀ Принимается при | Z|< U_α

1. Пусть утверждается что в генеральной совокупности рост студента составляет 175 см. по результатам выборочного обследования 100 человек. Установлено что выборочный средний рост составляет 178 см. Среднее квадратическое отклонение составляет 2 необходимо на уровне значимости 0,05 (5%) установить можно ли согласиться с данным утверждением

Н₀: =175

n=100

α= 0,05

Ϭ = 2 см

= 178

Назначаем альтернативную гипотезу

Н₁: >175

Z=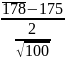 = 15

Ф(U_0,1) = 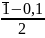= 0,45 => U_0,1= 1,65

2. Гипотеза о проверке среднего в генеральной совокупности при неизвестном генеральном среднем квадратическом отклонении

Н₀: =a₀

Ϭ – неизвестно

t=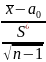

S* - исправленное выборочное среднее квадратическое отклонение

В зависимости от вида альтернативной гипотезы нулевая гипотеза принимается при выполнении условий

Н₁: < a₀ принимается при t> -t_2α

Н₂: < a₀ принимается при t< t_2α

Н₃: < a₀ принимается при |t|> t_α

t_2α, t_α – значение критических границ распределения Стьюдента с n-1 степенью свободы соответствующих 2α и α

Гипотеза о дисперсии генеральной совокупности

1. Н₁: Ϭ²= b₀

- известно

χ² =

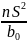
В зависимости от вида альтернативной гипотезы нулевая гипотеза принимается при выполнении условий

Н₁ * Ϭ² < b₀ χ² > 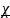²_α(n-1)

Н₂ * Ϭ² > b₀ χ² < 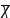²_α(n)

Н₃ * Ϭ² ≠ b₀ 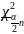< χ² <

²_{α(n) –} правосторонняя критическая граница с n степенями свободы отвечающая вероятности α

_α² – левосторонняя критическая граница

2. Н₁: Ϭ²= b₀

- неизвестно

χ² =

В зависимости от вида альтернативной гипотезы нулевая гипотеза принимается при выполнении условий

Н₁ * Ϭ² < b₀ χ² > ²_α(n-1)

Н₂ * Ϭ² > b₀ χ² < ²_α(n-1)

Н₃ * Ϭ² ≠ b₀ 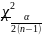< χ² <

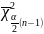
Гипотеза о вероятности наступления события в одном испытании (гипотеза о генеральной доле единиц обладающих исследуемым признаком)

Н₀: p=p₀ (некоторое число)

Z=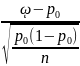

В зависимости от вида альтернативной гипотезы гипотеза H₀ принимается при выполнении условий

Н₁: p < p₀ принимается при | Z|> -U_2α

Н₂: p > p₀ принимается при | Z|< U_2α

Н₃: 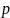≠ p₀ принимается при | Z|< U_α

При 100 подбрасываниях монетки выпало 55 решек можно ли на уровне значимости α=0,05 согласиться с теоретическим утверждением о том, что вероятность появления решки в одном испытании = 0,5

p₀ = 0,5

= 0,55

n=100

α=0,05

Н₀: p=0,5

Н₁: p ≠ 0,5

Z=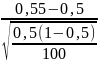 = 1 => U _α = 1,96

Гипотеза относительно законов распределения (непараметрических). Теории согласия.

Гипотеза относительно законов распределения предполагают использование для установления закономерностей в распределении тех или иных статистических признаков в этом случае нулевая статистическая гипотеза может звучать следующим образом

H₀: выборка извлеченная из генеральной совокупности подчиняющейся закону распределения F(X) – функциональная форма закона распределения

H₀: выборки извлечены из одной и той же генеральной совокупности

Указанные гипотезы проверяются с использованием специальных статистических критериев, которые называются критериями согласия.

Наиболее часто используемыми критериями согласия являются

1. Критерий Пирсона χ² – самый используемый. Сущность заключается в анализе расхождений между наблюдаемыми частотами и теоритическими частотами (теми частотами, которые наблюдались бы если бы выборка в точности подчинялась закону распределения F(x)

2. Критерий Колмагорова-Смирнова λ

3. Критерий фон Мизеса ῳ²

Алгоритм использование критерия Пирсона (χ²)

1. Всю совокупность выборочных значений разбивают на K непересекающихся групп или интервалов

2. Подсчитывается количество наблюдений f_i (i= 1….k) попавших в i-ю группу/интервал.

3. Предположив справедливость гипотезы H₀ определяют вероятность того, что значение признака будет принадлежать i-му интервалу/группе.

P₁=P(X [X_i-1,X₁)) = F(x_i) – F(x_i-1)

ϕ(x) = -функция распределения нормального закона

4. По вычисленным вероятностям P_i определяются значения теоретических частот f_i^’ = n* p_i

5. Если в каком-то из интервалов значение теоретической частоты оказалось менее 5 то производят объединение этого интернвала с соседними так чтобы для каждого из интервалов выполнялось условие f_i^’ > 5. Новое количество интервалов обозначают K*.

6. Для каждого из вновь образованных интервалов рассчитывают величину расхождения между эмпирическими и теоретическими частотами

χ² =

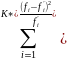
7. Полученную величину расхождения сравнивают с правосторонней критической границей χ² распределения соответствующей уровню значимости проверки гипотезы альфа при степенях свободы

m=k*-L-1

L – количество параметров/характеристик генеральной совокупности, оценивающихся по выборочным данным

8. Если выполняется условие χ²< χ^-2_a(m), то нулевая гипотеза принимается и говорится что выборка хорошо согласуется с выбранным законом распределения.

ПРИМЕР

Значение признака	Количество наблюдений	Вероятность(3 шаг) Pi	Теор частота (4 шаг)	расхождение (6 шаг)
190-192	1	0,0081	0,81	0,007
192-194	5	0,0385	3,85
149-196	10	0,1102	11,02
196-198	14	0,212	21,2	2,18
198-200	22	0,258	25,8	0,58
200-202	28	0,212	21,2	2,45
202-204	15	0,1102	11,02	1,074
206-208	5	0,0488	4,88
ИТОГ	100	1,00	100	6,291

Выборка извлечена из генеральной совокупности подчиняющейся нормальному закону распределения случайных величин

= 199

S = 3,0

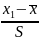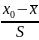P_i= Ф( ) - Ф( ) = 0,0081

Критерий Пирсона как критерий однородности выборок

При использовании χ² как критерии однородности выборок, нулевая критическая критерия звучит следующим образом

H₀: выборки извлечены из одной и той же генеральной совокупности.

Постановка задачи

Имеется L выборок каждый из которых имеет равный объем n₁,n₂…..n_L

Требуется проверить можно ли считать что выборки извлечены из одной и той же генеральной совокупности

Алгоритм использования критерия однородности χ²

1. Результаты первой, второй и т.д. L-й выборки группируют K-одинаковых групп или интервалов

2. Подсчитывают количество наблюдений f_ij (количество наблюдений i-й выборки попавших в j-ую группу/интервал). Данные представляют в виде групповой таблицы

3. Определить величину n_j по формуле. n_j=

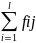
4. Определить суммарный объем наблюдений. n=

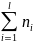
5. Рассчитываются вероятности принадлежности одного наблюдения к k-й группе интервалу

P_i=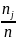 i=1….k

6. Расчитываются теоретические частоты - частоты которые наблюдались бы, если при полной однородности выбора

f_ij^’= p_jn_j=n_j

7. Рассчитывается мера расхождения между эмпирическими и теоретическими частотами

χ²=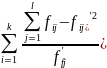

8. Рассчитанное значение χ² сравнивается с правосторонней критической границей распределения χ² отвечающей уровню значимости α при числе степеней свободы m=(l-1)(k-1)

ПРИМЕР: Для проведения респондентам задавался вопрос: будете ли вы принимать участие в выборах? Опрос проводился в дух регионах

Ответы	Номер региона		Nj
	1	2
Да	40	25	65
Нет	75	100	175
Итоги	115	125	240

P₁=65\240=0,27

P₂=175\240 = 0,73

t₁₁^’= P₁ n₁ = 0,27 * 115 = 31

t₁₂^’= 84

t₂₁^’= 34

t₂₂^’= 91

χ²= 81\31+81\34+81\84+81\91 = 6,9

При 5% степенях значимости и одной степени свободы

χ²_0,05(1)=3,84

Поскольку χ²-расчетная оказалась больше критического значения то гипотезу H₀ отвергнуть и считать что отношения к выборам в первом и втором регионе являются различным