Задача 1.1.

Для безынерционного звена, описываемого уравнением y(t) = kf(t), или ПФ W(s) = k при произвольно выбранном коэффициенте передачи k>0 определить переходную и частотные характеристики (АФХ и ЛЧХ).

Пусть k=6, W(s)=6

Переходная характеристика:

Частотные характеристики:

АФХ

ЛЧХ

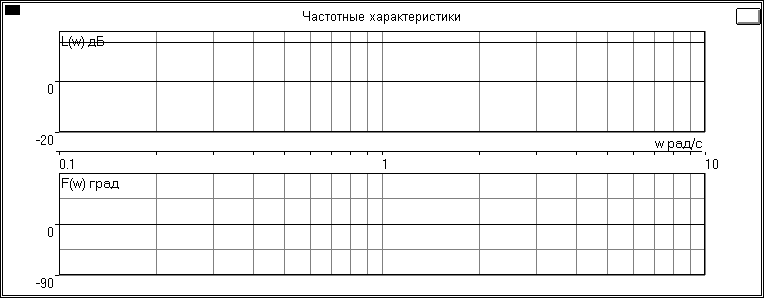
L(ω)=15,563025 дБ =20lg(6)

Ответить на следующие вопросы:

• На сколько дБ изменится значение ЛАЧХ, если коэффициент передачи увеличится в 10 раз?

Ответ: значение ЛАЧХ станет L(ω)=20lg(60)=35,563025 дБ, т.о. оно

увеличится на 20дБ т.е. на 20lg(10).

• Уменьшится в 2 раза?

Ответ: значение ЛАЧХ станет L(ω)=20lg(3)=9,542425 дБ, т.о. оно уменьшится на ≈6дБ ,т.е . на 20lg(1/2)

• Как влияет значение параметра k на фазовую характеристику?

Ответ: никак не влияет.

• Чему равен коэффициент передачи k, если значение ЛАЧХ равно -20 дБ?

L(ω)=20lg(k)

L(ω)=-20 дБ => k=0,1

Задача 1.2.

Для интегрирующего звена, описываемого ДУ вида

или ПФ

с любым положительным значением постоянной времени T (постоянная интегрирования) построить переходную и частотные характеристики (АФХ и ЛЧХ).

Пусть T=4=> W(s)=1/4s=0.25/s

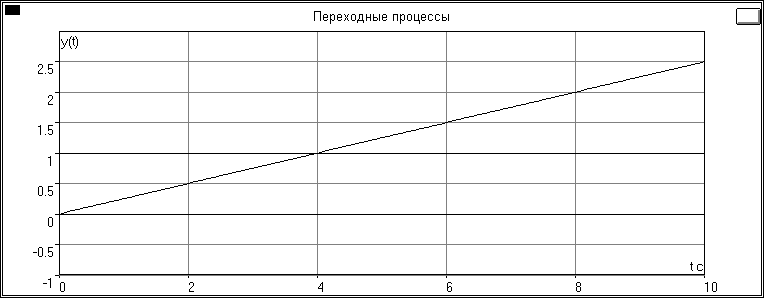
Переходная характеристика:

Частотные характеристики:

АФХ:

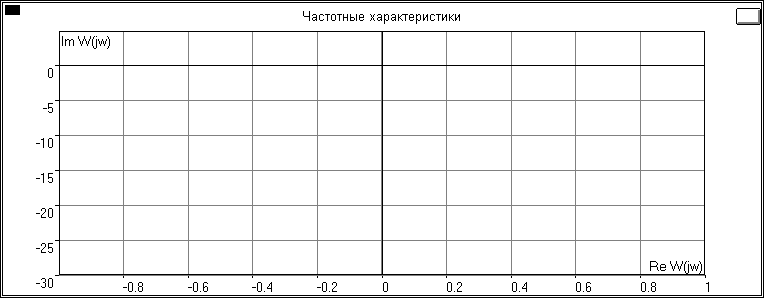
ЛЧХ:

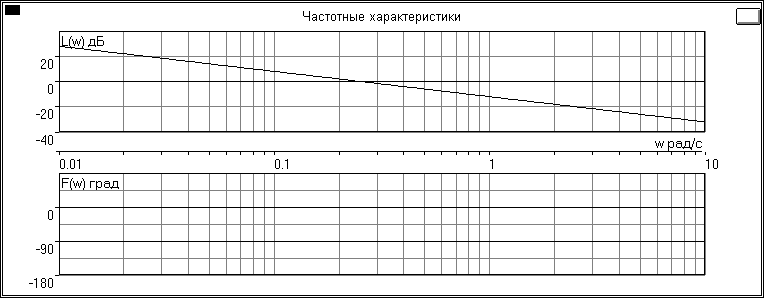
Ответить на следующие вопросы:

• Чему равно значение переходной характеристики h(t) при t = 1 c?

h(1)=0.25 т.к для интегрирующего звена h(1)=k*t k=0.25

T=4 t=1c h(1)=0.25

K=1/T

• Чему равны значения ЛАЧХ L() и ЛФЧХ () на частоте  = k = 1/T?

L(1/T)= L(0.25)=0 ,т.к. L(ω)=20lg(k)-20lg(ω)=

= 20lg(k/ ω)=[ω=1/T]=20lg(kT)=

=[k=1/T]=20lg(1)=0

(1/T)=-90град

• Как изменяются переходная характеристика и ЛАЧХ при увеличении постоянной интегрирования T в два раза?

переходная характеристика:

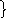h(t)=k*t

k=1/T =>при увеличении Т в 2 раза, k-коэф.наклона ПХ

уменьшается в 2 раза (1/4->1/8)

Частотные характеристики:

L(w) параллельно сдвинется вниз на 6 дБ ,т.к. ∆L(w)= 20lg(k1/ ω)- 20lg(k2/ ω) = 20lg(k1/k2)= [k2=2*k1] 20lg(1/2)=-6 дБ.

частота  = 1/T уменьшится в 2 раза, L(1/T)=0 , (1/T)=-90град

• Чему равна постоянная времени T, если L( = 10 c^-1) = -20 дБ?

L(10 c^-1) = -20 дБ

L(ω)=-20lg(Tω).

-20lg(10T)=-20 дБ => T=1с.

Задача 1.3.

Для дифференцирующего звена, описываемого уравнением вида

или ПФ

определить (для произвольного значения постоянной T) переходную и частотные характеристики (АФХ и ЛЧХ).

Пусть T=1/4=> W(s)=4s

Переходная характеристика:

Частотные характеристики:

АФХ

ЛЧХ

Ответить на следующие вопросы:

• Как отражается параметр T на переходной характеристике звена?

Пусть Т=6 вместо 4, тогда

т.о. происходит пропорциональное увеличение(уменьшение) значений ПХ, в зависимости от увеличения(уменьшения) Т, т.к. ПХ W(s)=Ts.

• Как изменяется ЛАЧХ при увеличении (уменьшении) параметра T в два раза?

При увеличении Т ω=1/Т уменьшится в 2 раза, ЛАЧХ сдвинется влево, при уменьшении –увеличится=>ЛАЧХ сдвинется вправо

L(w)=20lg(k*w)=> ∆L(w)=L1(w)-L2(w)=20lg(k1*w)-20lg(k2*w)=20lg(k1/k2)

k=1/T;

если k1>k2: т.е. T1<T2(увеличение Т в 2 раза),тогда

∆L(w)=20lg(k1/k2)=20lg((2*k2)/k2)=20lg(2)=6 дБ => ЛАЧХ

сдвинется параллельно вверх на 6 дБ.

если k1<k2: т.е. T1>T2(уменьшение Т в 2 раза),тогда

∆L(w)= 20lg(k1/k2)=20lg(k1/(2*k1))=20lg(1/2)=-6дБ => ЛАЧХ

сдвинется параллельно вниз на 6 дБ.

• Чему равно значение постоянной времени T, если L( = 2c^-1) = 0 дБ?

L(2 c^-1) =0 дБ

L(ω)=20lg(k)+20lg(ω).

lg(k)+lg(ω)=0

lg(k)=-lg(2)

lg(1/T)=lg(1/2)

=> T=2c