9. Методы статистического изучения взаимосвязи социально-экономических явлений.

Понятие причинности применяется всегда, когда осуществление одного события оказывается достаточным основанием для ожидания того, что произойдет другое событие. В этом случае первое событие выступает причиной, а второе - следствием.

В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, что позволяет выявлять факторы (признаки), оказывающие основное влияние на вариацию изучаемых массовых явлений и процессов.

В реальной действительности причину и следствие необходимо рассматривать как смежные явления, появление которых обусловлено комплексом сопутствующих более простых причин и следствий. Между сложными группами причин и следствий возможны многозначные связи, когда за одной причиной будет следовать то одно, то другое действие или одно действие имеет несколько различных причин. При изучении сложных процессов и явлений необходимо выявлять главные, основные причины, абстрагируясь от второстепенных.

Статистическое изучение связи между причиной и следствием состоит из нескольких этапов.

На первом этапе изучается качественный анализ рассматриваемого явления, связанный с анализом природы явления. На втором этапе строится модель связи. Этот этап базируется на методах статистики: группировках, средних величинах, таблицах и т.д. На третьем, последнем этапе осуществляется интерпретация результатов. Этот этап так же, как и первый, связан анализом природы изучаемого явления.

Корреляция - это статистическая зависимость между величинами, не имеющая строго функционального характера, при которой изменение одной из случайных величин приводит к изменению другой величины.

В статистике принято различать следующие варианты зависимостей:

1. Парная корреляция - связь между двумя признаками (результативным и факторным или между двумя факторными);

2. Частная корреляция - зависимость между результативным и одним факторным признаком при фиксации значений других факторных признаков;

3. Множественная корреляция - зависимость результативного и двух или более факторных признаков, включенных в исследование.

Графически взаимосвязь двух признаков изображается с помощью поля корреляции. В системе координат на оси абсцисс откладываются значения факторного признака, а на оси ординат - результативного. Точки с соответствующими абсциссами и ординатами наносятся на плоскость. При отсутствии тесных связей имеет место беспорядочное расположение точек на графике. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии.

Корреляционный анализ имеет своей задачей количественное определение тесноты связи между признаками: при парной корреляции - между двумя признаками; при множественной корреляции - между несколькими.

Корреляционный анализ изучает взаимозависимости показателей и позволяет решить следующие задачи:

1. Задача оценки тесноты связи между показателями с помощью парных, частных и множественных коэффициентов корреляции;

2. Задача оценки уравнения регрессии.

Основной предпосылкой применения корреляционного анализа является необходимость подчинения совокупности значений всех факторных признаков (Х1, Х2, ...Хк) и результативного признака (У) нормальному закону распределения или близость к нему. Если объем исследуемой совокупности большой и превышает 50 наблюдений, то нормальность распределения может быть подтверждена на основе расчета и анализа специальных критериев: Пирсона, Ястремского, Боярского, Колмогорова и пр. Если объем совокупности меньше 50, то закон распределения исходных данных определяется на базе построения и визуального анализа поля корреляции. При этом если в расположении точек имеет место линейная тенденция, то можно предположить, что совокупность исходных данных (У, Х1,Х2,...Хк) подчиняется нормальному распределению.

Целью регрессионного анализа является оценка функциональной зависимости условного среднего значения результативного признака (У) от факторных (Х1, Х2, ..., Хк).

Основной предпосылкой регрессионного анализа является то, что только результативный признак (У) подчиняется нормальному закону распределения, а факторные признаки Х1, Х2, ..., Хк могут иметь произвольный закон распределения. В динамических рядах в качестве фактора выступает время. При этом в регрессионном анализе заранее подразумевается наличие причинно-следственных связей между результативным (У) и факторными (Х1, Х2, ..., Хк) признаками.

Уравнение регрессии, или статистическая модель связи массовых процессов и явлений, выражаемая функцией

Ух = Ф (Х1, Х2, ..., Хк), является достаточно адекватным реальному моделируемому явлению или процессу в случае соблюдения следующих требований их построения:

1. Совокупность исследуемых исходных данных должна быть однородной и математически описываться непрерывными функциями;

2. Возможность описания моделируемого явления одним или несколькими уравнениями причинно-следственных связей;

3. Все факторные признаки должны иметь количественное (цифровое) выражение;

4. Наличие достаточно большого объема исследуемой выборочной совокупности;

5. Причинно-следственные связи между явлениями и процессами следует описывать линейной или приводимой к линейной формами зависимости;

6. Отсутствие количественных ограничений на параметры модели связи;

7. Постоянство территориальной и временной структуры изучаемой совокупности.

Соблюдение данных требований позволяет исследователю построить статистическую модель связи, наилучшим образом аппроксимирующую моделируемые массовые процессы и явления.

Теоретическая обоснованность моделей взаимосвязи, построенных на основе корреляционно-регрессионного анализа, обеспечивается соблюдением следующих основных условий:

а. Все признаки и их совместное распределение должны подчиняться нормальному закону распределения;

б. Дисперсия моделируемого признака (У) должна все время оставаться постоянной при изменении величины У и значений факторных признаков;

в. отдельные наблюдения должны быть независимыми, то есть результаты, полученные в к-ом наблюдении, не должны быть связаны с предыдущими и содержать информацию о последующих наблюдениях, а также не влиять на них.

Отступление от выполнения этих (а. - в.) условий и предпосылок приводит к тому, что параметры регрессии не будут отражать реальное воздействие на моделируемый показатель.

Основной проблемой построения уравнения регрессии является его размерность, то есть определение числа факторных признаков, включаемых в модель. Их число должно быть оптимальным, то есть наилучшим. Сокращение размерности за счет исключения второстепенных, несущественных факторов позволяет получить модель, реализуемую быстрее и качественнее. В то же время построение модели малой размерности может привести к тому, что она будет недостаточно полно описывать исследуемое явление или процесс.

Практикой выработаны определенные критерии, позволяющие установить оптимальное соотношение между числом факторных признаков, включаемых в модель, и объемом исследуемой совокупности. Согласно данному критерию число факторных признаков (к) должно быть в 5 - 6 раз меньше объема изучаемой совокупности.

Построение корреляционно-регрессионных моделей, какими бы сложными они не были, само по себе не вскрывает полностью всех причинно-следственных связей. Основой их адекватности является предварительный качественный анализ, основанный на учете специфики и особенностей сущности исследуемых массовых процессов и явлений.

Парная регрессия характеризует связь между двумя признаками: результирующим и факторным. Аналитическая форма записи этой связи имеет вид:

прямая -

гиперболы -

параболы -

Определить тип уравнения можно, первоначально исследуя зависимость графически. Однако существуют также более общие указания, позволяющие выявить уравнение связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, примерно в арифметической прогрессии, то это свидетельствует о том, что связь между ними линейная, а при обратной связи - гиперболическая. Если факторный признак изменяется значительно быстрее результативного, то используется степенная регрессия. Если же результативный признак изменяется значительно быстрее факторного, то используется параболическая или степенная регрессионная зависимости.

Оценка параметров уравнений регрессии осуществляется методом наименьших квадратов (МНК), в основе которого лежит предположение о независимости наблюдений исследуемой совокупности.

Сущность МНК состоит в том, что ищутся параметры модели , при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, то есть полученных по выбранному уравнению регрессии:

где Y - фактическое значение признака;

- теоретическое значение признака.

Для прямой зависимости это выглядит так:

Из курса математики известно, что функция достигает своего минимума, когда равны нулю ее производные. Производные берутся по параметрам и . Так как и не заданы, то именно они являются неизвестными и должны быть определены.

Откуда система нормальных уравнений для нахождения параметров линейной регрессии имеет следующий вид:

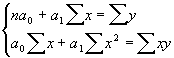
где n - число наблюдений.

В уравнениях регрессии параметр показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов; а параметр (в уравнении параболы и ) - коэффициент регрессии показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения (то есть скорость изменения результативного при изменении на единицы факторного признака).

Существуют другие методы минимизации ошибки (разности между теоретическим значением результирующего фактора и его фактическим значением). Однако наиболее оптимальным вариантом является оценка ошибки по МНК. Этот метод обладает тем замечательным свойством, что делает число нормальных уравнений равным числу неизвестных коэффициентов.

Оценка существенности связи

Проверка адекватности модели регрессии, построенной на основе того или иного уравнения связи, начинается с проверки значимости каждого коэффициента регрессии.

Оценка значимости коэффициентов регрессии осуществляется с помощью t- критерия Стьюдента:

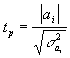
где - дисперсия коэффициента регрессии.

Параметр модели регрессии признается статистически значимым, если выполняется неравенство:

( ; =n-k-1)

где - уровень значимости критерия проверки гипотезы о равенстве нулю параметров, измеряющих связь, то есть статистическая существенность связи утверждается (признается) при отклонении нулевой гипотезы об отсутствии связи;

=n-k-1 - число степеней свободы, которое характеризует число свободно варьирующих элементов совокупности.

Дисперсия коэффициента регрессии может определяться одним из двух способов:

где - дисперсия результативного признака;

- число факторных признаков в уравнении.

Или:

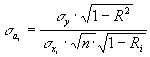
где - величина множественного коэффициента корреляции по фактору с остальными факторами;

- среднее квадратическое отклонение рассматриваемого фактора;

- среднее квадратическое отклонение результирующего фактора.

Проверка адекватности всей модели осуществляется с помощью расчета F -критерия и величины средней ошибки аппроксимации.

Если средняя ошибка аппроксимации не превышает 12 - 15%, то уравнение построено верно.

При проверке адекватности уравнения регрессии исследуемому процессу возможны следующие варианты:

1. Построенная модель на основе ее проверки по критерию Фишера в целом адекватна, и все коэффициенты регрессии значимы. Такая модель может быть использована для принятия решений к осуществлению прогнозов.

2. Модель по критерию Фишера адекватна, но часть коэффициентов регрессии незначима. В этом случае модель пригодна для принятия некоторых решений, но не для прогнозов.

3. Модель по критерию Фишера адекватна, но все коэффициенты регрессии незначимы. Модель в этом случае отвергается. На ее основе никаких решений проводит нельзя.

Наиболее сложным этапом, завершающим регрессионный анализ, является интерпретация уравнения регрессии, то есть перевод его с языка статистики и математики на содержательный уровень.

С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле:

где - среднее значение соответствующего факторного признака;

- среднее значение результативного признака;

- коэффициент регрессии при соответствующем факторном признаке.

Частный коэффициент детерминации также используется для расширения возможностей содержательного анализа модели регрессии. Он рассчитывается по формуле:

где - парный коэффициент корреляции между результативным и i - факторным признаком;

- соответствующий коэффициент уравнения множественной регрессии в стандартизованной форме.

Частный коэффициент детерминации показывает, на сколько процентов вариация результативного признака объясняется вариацией i - го признака, входящего в множественное уравнение регрессии.

Рассчитываются также множественный коэффициент детерминации, который представляет собой множественный коэффициент корреляции в квадрате. Он характеризует, какая доля вариации результативного признака обусловлена изменением факторных признаков, входящих в многофакторную модель.

Рассчитываются также некоторые другие коэффициенты, позволяющие интерпретировать модель регрессии.

Отрицательными свойствами уравнений регрессии являются:

-хорошо аппроксимируются только те значения результативного признака, которые стоят в середине вариационного ряда индивидуальных значений. Ошибка аппросимации не превышает 1 - 2%;

-ошибка аппроксимации на концах исходного ряда может достигать 50%;

-уравнения регрессии пригодны только для краткосрочных прогнозов;

-на основе уравнения регрессии невозможно получить оптимального значения моделируемого показателя.

Непараметрические показатели связи

Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи массовых процессов и явлений. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака от одного или нескольких факторов.

Для оценки тесноты и существенности связи между двумя коррелированными признаками используется линейный коэффициент корреляции. Этот коэффициент был введен в начале 90-х годов Пирсоном, Эджвортом и Велдоном. В практике применяются различные математические формулировки этого коэффициента. Приведем три из них:

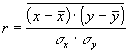
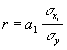
Линейный коэффициент корреляции изменяется в пределах от -1 до 1. Знаки коэффициентов регрессии и корреляции совпадают.

Для измерения тесноты связи используются также и другие показатели: корреляционное отношение (эмпирическое и теоретическое); множественный коэффициент корреляции; частные коэффициенты корреляции и некоторые другие.

Ранговые коэффициенты связи

В анализе массовых процессов и явлений часто приходится прибегать к различным условным оценкам, которые называются рангами, а взаимосвязь между отдельными признаками измерять с помощью непараметрических коэффициентов связи. Эти коэффициенты исчисляются при условии, что исследуемые признаки подчиняются различным законам распределения.

Ранжирование - процедура упорядочивания объектов изучения, которая выполняется на основе предпочтения.

Ранг - порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической от соответствующих номеров мест, которые они определяют. Данные ранги называются связными.

Среди непараметрических методов оценки тесноты связи наибольшее значение имеют ранговые коэффициенты Спирмена ( ) и Кендала ( ). Эти коэффициенты могут быть использованы для определения тесноты связей как между количественными, так и между качественными признаками при условии, если их значения упорядочить или проранжировать по степени убывания или возрастания признака.

Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывается для случаев, когда нет связных рангов. Его формула:

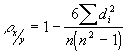
где - квадрат разности рангов;

n - число наблюдений (число пар рангов).

Коэффициент Спирмена принимает любые значения в интервале (-1;1) . Значимость коэффициента корреляции рангов Спирмена проверяется на основе критерия Стьюдента.

Расчет коэффициента Спирмена осуществляется по следующему алгоритму. Сначала ранжируются значения результирующего признака. Затем ранжируются значения факторного признака. Значения рангов парных признаков : результирующего и факторного сравниваются, вычисляется разница рангов, которая возводится в квадрат и далее подставляется в формулу.

Ранговый коэффициент корреляции Кендалла может использоваться для измерения взаимосвязи между качественными и количественными признаками, характеризующими однородные объекты. Ранжированные по одному принципу. Расчет рангового коэффициента Кендалла осуществляется по формуле

где n- число наблюдений;

S - сумма разностей между числом последовательностей и числом инверсий по второму признаку. S = P + Q

Расчет данного коэффициента выполняется в следующей последовательности:

1) значения Х ранжируются в порядке возрастания или убывания;

2) значения У располагаются в порядке, соответствующем значениям Х;

3) для каждого ранга У определяется число следующих за ним рангов, превышающих его величину. Суммируя таким образом числа, определяется величина Р как мера соответствия последовательностей рангов Х и У и учитывается со знаком (+);

4) для каждого ранга У определяется число следующих за ним рангов, меньших его величины. Суммарная величина обозначается через Q и фиксируется со знаком (-);

5) определяется сумма баллов по всем членам ряда.

Формула Кендалла используется и для связных рангов.

Как правило коэффициент Кендалла меньше коэффициента Спирмена.

Связь между признаками можно признать статистически значимой, если значения коэффициентов ранговой корреляции Спирмена и Кендалла больше 0.5.

Для определения тесноты связи между произвольным числом ранжированных признаков применяется множественный коэффициент ранговой корреляции (коэффициент конкордации) (W), который вычисляется по формуле:

где m - количество факторов;

n - число наблюдений;

S - отклонение суммы квадратов рангов от средней квадратов рангов.

Коэффициент конкордации принимает любые значения в интервале (-1;1) .

Ранговые коэффициенты корреляции Спирмена, Кендалла и конкордации обладают тем преимуществом, что с их помощью можно измерять и оценивать связи как между количественными, так и между атрибутивными признаками, которые поддаются ранжированию.