5. Перевірка значимості параметрів регресійної моделі за допомогою t-критерію Ст’юдента

Для перевірки на значимість параметрів регресійної моделі, при умові, що вона адекватна дійсній, потрібно спочатку знайти оцінку дисперсії залишків (помилок):

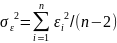
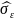називають стандартною помилкою рівняння регресії.

Тож потрібно знайти дисперсійно-коваріаційну матрицю параметрів моделей регресії:

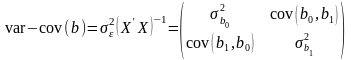
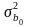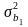, - оцінки параметрів дисперсії

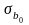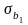, - стандартні похибки коефіцієнтів

Алгоритм перевірки значимості коефіцієнта

лінійної регресії

1. Висувають статистичні гіпотези:

2. Задають критерій:

( )

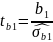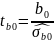Вважають, що цей критерій має розподіл Ст’юдента (t-розподіл) з

3. Знаходять фактичне значення критерію ( ).

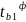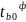4. Знаходять за таблицями t-розподілу 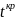для рівня значимост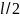і і 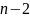ступенів вільності.

5. Порівнюють між собою два знайдені значення.

Якщо 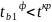( 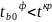) тоді приймається нульова гіпотеза і коефіцієнт ( ) вважається статистично не значимий, тобто його моделі можна опустити (відкинути). В противному випадку коефіцієнт ( ) вважають статистично значимим при прийнятті альтернативної гіпотези.

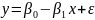
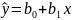- вибіркова модель

Зауваження: функція розподілу Ст’юдента або t-розподілу має вигляд: (графік).

Перевірка значимості коефіцієнта кореляції за допомогою

t-критерію Ст’юдента.

Перевірка на значимість вибіркового коефіцієнта кореляції здійснюється за допомогою t-критерію Ст’юдента.

Для перевірки вибирають критерій:

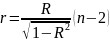
Вважають, що цей критерій має розподіл Ст’юдента з 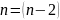ступенями вільності. Гіпотези мають вигляд:

Якщо приймається нульова гіпотеза, то вважають, що між змінними у та х не існує лінійної залежності. При гіпотезі вважається, що така залежність між у та х існує.

Якщо отримана вибіркова модель лінійної регресії адекватна дійсній моделі, оцінки параметрів статистично значимі та між змінними х та у існує лінійний зв'язок, то цю вибіркову модель можна використати для дослідження процесу, який вона описує. Дослідження полягає в тому, щоб встановити рівень впливу, в певному розумінні, незалежної змінної на залежну, а також можливі значення різного типу прогнозованих значень у.

6. Коефіцієнт еластичності. Довірчі інтервали (інтервали довіри). Прогнозування за допомогою моделі парної лінійної регресії

Середнім коефіцієнтом еластичності моделі парної регресії називається величина:

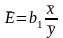
Цей коефіцієнт показує на скільки процентів (відсотків) зміниться змінна у, якщо змінна х зміниться (збільшиться) на 1 процент (відсоток).

Довірчі інтервали (інтервали довіри)

Якщо для регресійної моделі 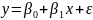отримати вибіркову регресійну модель 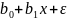, то тоді за знайденими оцінками параметрів моделі можна знайти інтервали, які з деякою імовірністю попадають в невідомі параметри . Ці інтервали називаються довірчими інтервалами або інтервалами довіри.

Інтервал довіри (довірчий інтервал) – це інтервал, в який з ймовірністю 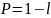( – рівень значимості, Р – рівень надійності) попадає в параметр при знайдених оцінках параметрів при заданому рівні значимості .

Інтервали довіри мають вигляд:

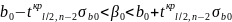
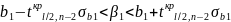
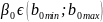
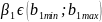
(графік)

Геометрична інтерпретація:

Якщо полоса між прямими 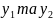є неширокою, це означає, що оцінки параметрів досить добре наближають дійсні значення параметрів моделі .

Прогнозування за допомогою моделі парної лінійної регресії

Для регресійних моделей використовують в основному два типи прогнозів: точковий та інтервальний.

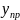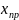Точковий прогноз – дає змогу знайти прогнозоване значення , якщо задане прогнозоване значення . Прогнозоване значення знаходять за формулою:

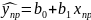
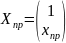
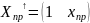
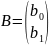
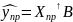
Інтервальний прогноз задає інтервал, який з ймовірністю попадає в дійсне значення змінної у при заданому рівні значимості .

Інтервальний прогноз знаходиться наступним чином: