
- •1. Оцінка параметрів лінійної регресії методом найменших квадратів
- •2. Коефіцієнт кореляції та детермінації
- •3. Властивості оцінок параметрів лінійної регресії
- •4. Перевірка лінійної регресії на адекватність (значимість) за допомогою f-критерію Фішера.
- •5. Перевірка значимості параметрів регресійної моделі за допомогою t-критерію Ст’юдента
- •6. Коефіцієнт еластичності. Довірчі інтервали (інтервали довіри). Прогнозування за допомогою моделі парної лінійної регресії
- •7.Нелінійна регресія
- •8. Поняття мультиколінеарності, основні її ознаки та наслідки
- •9. Методи усунення мультиколінеарності
- •10. Алгоритм Фарара-Глобера
- •11. Поняття гетероскедастичності та її наслідки
- •12. Тест Голдфельда-Квандта
- •13. Знаходження оцінок параметрів моделі за допомогою узагальненого методу найменших квадратів (метод Ейткена)
- •14. Поняття автокореляції та її наслідки
- •15. Критерій Дарбіна-Уотсона
- •16. Оцінювання параметрів економетричної моделі узагальненим методом найменших квадратів при наявності автокореляції
1. Оцінка параметрів лінійної регресії методом найменших квадратів
Існують
різні методи знаходження оцінок
параметрів
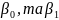 .
Розглянемо один із них: метод найменших
квадратів.
.
Розглянемо один із них: метод найменших
квадратів.
Суть
методу: оцінки парламентів
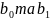 знаходять так, щоб сума квадратів
відхилень (помилок) між заданими
значеннями змінної у і розрахунковими
була найменшою. Похибка між заданими
значеннями і розрахунковими має вигляд:
знаходять так, щоб сума квадратів
відхилень (помилок) між заданими
значеннями змінної у і розрахунковими
була найменшою. Похибка між заданими
значеннями і розрахунковими має вигляд:

Функція квадрату похибок має вигляд:
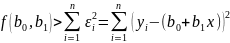
Функція
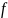 залежить
від змінних параметрів
,
для знаходження її найменшого значення
потрібно знайти критичні її точки. Для
цього потрібно знайти частинні похідні,
прирівняти їх до 0 і знайти розв’язок
отриманої системи рівнянь
(3).
залежить
від змінних параметрів
,
для знаходження її найменшого значення
потрібно знайти критичні її точки. Для
цього потрібно знайти частинні похідні,
прирівняти їх до 0 і знайти розв’язок
отриманої системи рівнянь
(3).
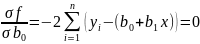

Отримана система (3) є лінійною системою рівняння для знаходження оцінок параметрів (4)
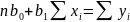
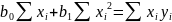
Введемо позначення:
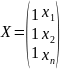
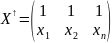
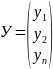
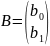
Система (4) в матричному вигляді:
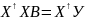 (5)
(5)
Система (5) називається нормальною системою рівняння для рівняння лінійної регресії.
Матрицю
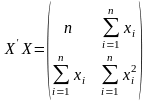 називають матрицею спостереження. Вона
завжди має симетричний вигляд.
називають матрицею спостереження. Вона
завжди має симетричний вигляд.
Із рівняння (5) отримаємо оцінки параметрів лінійної регресії:
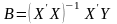 (6)
(6)
Зауваження:
оцінки параметрів лінійної регресії
методами найменших квадратів знаходять
при умові, що випадкова складова
економетричної моделі
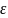 задовольняє певним умовам.
задовольняє певним умовам.
Оцінки параметрів моделі можна обчислити за наступними формулами (7):
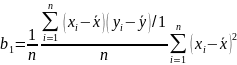
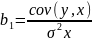
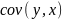 – величина,
яка показує залежність змінної у до х
по відношенню до своїх середніх значень.
– величина,
яка показує залежність змінної у до х
по відношенню до своїх середніх значень.
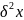 -
визначає середній квадрат відношень
значень змінної х по відношенню до своїх
середніх значень.
-
визначає середній квадрат відношень
значень змінної х по відношенню до своїх
середніх значень.
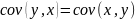
Оцінки
параметра
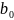 можна обчислити за формулою:
можна обчислити за формулою:
 (8)
(8)
Зауваження:
Для оцінки параметрів знайдені методом найменших квадратів, тоді сума всіх похибок (залишок відхилень) дорівнює 0.
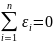
Вибіркова
регресійна пряма завжди проходить через
середню точку (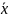 ,
,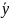 ).
).
З
вибіркового регресійного рівняння:
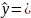
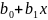 отримуємо значення
отримуємо значення
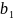 рівне величині на яку збільшується
залежна змінна у при збільшенні незалежної
змінної х на 1.
рівне величині на яку збільшується
залежна змінна у при збільшенні незалежної
змінної х на 1.
Величина називається перетином, а – нахилом рівняння регресії.
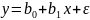
2. Коефіцієнт кореляції та детермінації
Якщо побудована вибіркова регресійна модель, то виникають наступні задачі:
Чи в дійсності існує лінійний зв'язок між змінними х та у.
Наскільки отримана модель адекватна (відповідає) дійсній моделі.
Наскільки точно знайдені оцінки параметрів моделі.
Як можна здійснити прогноз за побудованої регресійною моделлю.
Кількісним критерієм, який оцінює тісноту зв’язку між х та у є вибірковий коефіцієнт кореляції, який обчислюється за формулою:
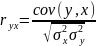
Значення
коефіцієнта кореляції знаходиться в
межах від
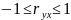 .
.
Якщо
 ,
то вважають, що між змінними у та х існує
прямий зв'язок, якщо
,
то вважають, що між змінними у та х існує
прямий зв'язок, якщо
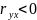 ,
то зворотній (обернений зв'язок).
,
то зворотній (обернений зв'язок).
Якщо
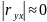 ,
тоді змінна х істотно не впливає на
змінну у. В цьому випадку потрібно
вибрати (знайти) іншу змінну, яка більш
істотно впливає на змінну у.
,
тоді змінна х істотно не впливає на
змінну у. В цьому випадку потрібно
вибрати (знайти) іншу змінну, яка більш
істотно впливає на змінну у.
Якщо
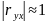 ,
тоді вважають, що між х
та у
існує тісний зв'язок (залежність).
,
тоді вважають, що між х
та у
існує тісний зв'язок (залежність).
Для встановлення чинності зв’язку між змінними х і у та перевірки на адекватність (значимість) моделі парної регресії реального економічного процесу використовують вибірковий коефіцієнт детермінації, який обчислюється за формулою:
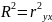
Якщо
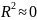 ,
то вважають, що побудована регресійна
модель неадекватна дійсній моделі
(дійсному процесу).
,
то вважають, що побудована регресійна
модель неадекватна дійсній моделі
(дійсному процесу).
Якщо
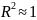 ,
то вважають, що отримана модель адекватна
дійсній моделі, тобто є значимою.
,
то вважають, що отримана модель адекватна
дійсній моделі, тобто є значимою.
