1.Разложение дробно-рац. Фун-ии на простейшие дроби
Метод неопределенных коэффициентов является универсальным способом при разложении дроби на простейшие.
Алгоритм метода неопределенных коэффициентов.
Во-первых, раскладываем знаменатель на множители.
Здесь все методы хороши – от вынесения за скобки, применения формул сокращенного умножения, до подбора корня и последующего деления столбиком (при знаменателе в виде многочлена с рациональными коэффициентами степени выше второй).
Во-вторых, раскладываемую дробь представляем в виде суммы простейших дробей с неопределенными коэффициентами. (Возьмите на заметку: какая степень – столько и слагаемых.)
В-третьих, приводим полученную сумму простейших дробей с неопределенными коэффициентами к общему знаменателю и группируем в числителе слагаемые при одинаковых степенях х.
В-четвертых, приравниваем коэффициенты при одинаковых степенях х.
В-пятых, решаем полученную систему уравнений любым способом
В-шестых- ответ
Про таблицу первообразных можно сказать
2. Первообразная функции. Неопределенный интеграл и его свойства.
Функция
F, заданная на некотором промежутке D,
называется первообразной функции f,
заданной на том же промежутке, если для
любого
F’(x)=f(x).
Например функция Х в третьей степени
деленное на 3 является первообразной
для функции х в квадрате.
Множество
всех первообразных некоторой функции
f(x) называется неопределенным интегралом
функции f(x) и обозначается как
,
Таким образом, если F - некоторая частная
первообразная, то справедливо выражение
где
С- произвольная постоянная.
Свойства неопределенного интеграла
В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f,
а, k, C - постоянные величины.
Ну еще можно сказать про таблицу интегралов
3. Интегралы от основных элементарных функций.
Интегрирование — это одна из двух основных операций в математическом анализе, но в отличие от операции дифференцирования она выводит из множества элементарных функций.
Интегралы элементарных функций
Рациональные функции
Логарифмы
Иррациональные функции
Тригонометрические функции
4. Методы интегрирования: замена переменной, интегрирование по частям.
Метод
интегрирования подстановкой заключается
во введении новой переменной интегрирования
(то есть подстановки). При этом заданный
интеграл приводится к новому интегралу,
который является табличным или к нему
сводящимся. Общих методов подбора
подстановок не существует. Замена
переменной в неопределенном интеграле
производится с помощью подстановок
двух видов: а)х= фита(t)
где фита(t)
– монотонная, дифференцируемая функция;
б)
,где
– новая переменная.
В первом случае формула замены переменной имеет вид:
(6.1)
Во втором случае:
(6.2)
В обоих случаях после интегрирования следует возвращаться к старой переменной обратной подстановкой.
Интегрирование по частям: Интегрирование по частям. Если функции u ( x ) и v ( x ) имеют непрерывные первые производные и существует интеграл v ( x ) du ( x ), то существует и интеграл u ( x ) dv ( x ) и имеет место равенство: (значок интеграла) u dv = u v – (значок интеграла) v du
5.Интегрирование простейших рациональных дробей
Все, по методу плавающих коэффициентов, первый билет.
Для
интегрирования рациональной функции
,
где P(x) и Q(x) - полиномы, используется
следующая последовательность шагов:
Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение;
Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;
Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;
Вычислить интегралы от простейших дробей.
6. Интегрирование некоторых видов иррациональностей
Не знаю.
7. Тригонометрические подстановки.
Универсальная
тригонометрическая подстановка. Переход
в подынтегральной функции к переменной
преобразует R(sin
x, cos x) в функцию, рационально зависящую
от t. Универсальная тригонометрическая
подстановка всегда рационализирует
подынтегральную функцию, с её помощью
легко берутся интегралы вида
(a, b, c - постоянные); однако часто она
приводит к очень громоздким рациональным
дробям, у которых, в частности, практически
невозможно найти корни знаменателя.
Поэтому при возможности применяются
частные подстановки, которые тоже
рационализируют подынтегральную функцию
и приводят к менее сложным дробям.
Пример:
..
8. Интегрирование тригонометрических функций.
.Интегралы
вида
вычисляются преобразованием произведения
тригонометрических функций в сумму по
формулам:
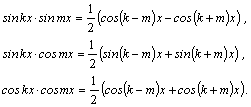
Интегралы
вида
,
где m или n– нечетное положительное
число, вычисляются подведением под знак
дифференциала.
Интегралы
вида
, где m и n–четные положительные числа,
вычисляются с помощью формул понижения
степени:
.Интегралы
где
вычисляются заменой переменной
:или
.Интегралы
вида
сводятся к интегралам от рациональных
дробей с помощью универсальной
тригонометрической подстановки.
9. Определенный интеграл: определение, свойства, геометрический смысл.
Определённый
интеграл — аддитивный монотонный
нормированный функционал, заданный на
множестве пар, первая компонента которых
есть интегрируемая функция или функционал,
а вторая — область в множестве задания
этой функции (функционала).определение
интеграла при всей его кажущейся общности
в итоге приводит к привычному пониманию
определённого интеграла, как площади
подграфика функции на отрезке.
Определённый
интеграл
численно равен площади фигуры,
ограниченной осью абсцисс, прямыми х=а
и х=в и графиком функции f(x).
Свойства интеграла:
1.Величина
определенного интеграла не зависит от
обозначения переменной интегрирования,
т.е.
,
где х, t – любые буквы.
2.Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
3. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
4.
Если промежуток
интегрирования [a,b] разбит на конечное
число частичных промежутков, то
определенный интеграл, взятый по
промежутке [a,b], равен сумме определенных
интегралов, взятых по всем его частичным
промежуткам.
5. Постоянный множитель можно выносить за знак определенного интеграла.
6.
Определенной
интеграл от алгебраической суммы
конечного числа непрерывных функций
равен такой же алгебраической сумме
определенных интегралов от этих функций.
10. Определенный интеграл с переменным верхним пределом. Вычисление определенного интеграла: формула Ньютона-Лейбница.
Рассмотрим
функцию y = f(x), интегрируемую на отрезке
[а, b]. Если х на промежутке [a, b], то функция
f(x) интегрируема также на любом отрезке
[а, х]. Предположим, что х меняется на
отрезке [а, b], тогда на этом отрезке
определена функция. (Переменную
интегрирования обозначили буквой t,
переменный верхний предел - буквой х).
Теорема 1. Если функция у = f(x) интегрируема на отрезке [а, b], то функция Ф(х) непрерывна на этом отрезке.
Теорема
2. Если подынтегральная функция непрерывна,
то производная определенного интеграла
с переменным верхним пределом существует
и равна значению подынтегральной функции
для этого предела. т.е.
Следствие
1. Если функция f(x) непрерывна на отрезке
[а, b], то при любом х
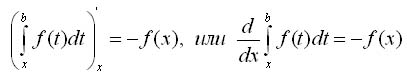
Следствие 2. Определенный интеграл с переменным верхним пределом является одной из первообразных для непрерывной подынтегральной функции.
Другими словами, для любой непрерывной функции существует первообразная.
Эти функции не являются элементарными; первообразные указанных подынтегральных функций не выражаются через элементарные функции.
Все приведенные функции хорошо изучены, для них составлены таблицы значений, эти функции находят широкое применение.
Связь между определенными и неопределенными интегралами выражает следующая теорема Ньютона - Лейбница, называемая основной теоремой интегрального исчисления.
Теорема
3. Определенный интеграл от непрерывной
функции равен разности значений любой
ее первообразной для верхнего и нижнего
предела интегрирования:
Эта
формула называется формулой Ньютона -
Лейбница; ее можно переписать в виде
,
левая часть второй формулы читается
так: «двойная подстановка от а до b для
функции F(x).
11. Приложения определенного интеграла.
Тоже не знаю.
12. Несобственные интегралы.
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:
Предел a или b (или оба предела) являются бесконечными;
Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].
13.Дифференциальные уравнения, основные понятия.
Дифференциальное уравнение — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, её производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением.
Порядок,
или степень дифференциального уравнения
— наибольший порядок производных,
входящих в него. Решением
(интегралом) дифференциального уравнения
порядка n называется функция y(x), имеющая
на некотором интервале (a, b) производные
до порядка n включительно и удовлетворяющая
этому уравнению.