3.3. Биномиальный закон распределения
Пусть производятся повторные независимые
испытания: подбрасывание монеты,
измерение температуры, рождение детей
стрельба по цели и
т.п., А – событие, которое может
появиться в результате каждого
испытания; для каждого единичного
испытания Р(А) = р; Р(
)
= q = 1 – р;
n – количество независимых повторных испытаний, К – число появления события А: Х = К – биномиальная случайная величина, она дискретна. Ее значения: К = 0; 1; 2; …
Соответствующие им вероятности находим по формуле Бернулли:
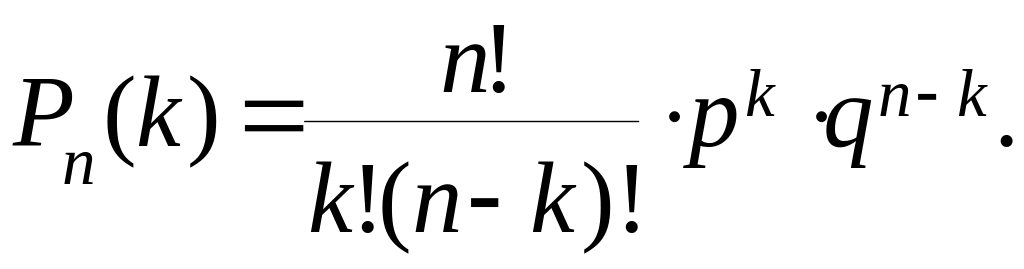
Закон распределения биномиальной случайной величины:
Х |
0 |
1 |
2 |
… |
n |
Р(Х=К) |
Pn(0) |
Pn(1) |
Pn(2) |
… |
Pn(n) |
Pn(0)
+ Pn(1)
+ Pn(2)
+ … +
Pn(n)
=
Основные характеристики биномиальной случайной величины:
M(X) = np; D(X) = npq; 
Пример. Вероятность попадания в цель при одном выстреле 0,8. Составить закон распределения числа попаданий в цель при пяти выстрелах.
Решение. р = 0,8; q = 1 – 0,8 = 0,2; n = 5; k = 0; 1; 2; 3; 4; 5.
Х=К |
0 |
1 |
2 |
3 |
4 |
5 |
Р5(к) |
q5= =0,00032 |
5q4р= =0,0064 |
10q3р2= =0,0512 |
10q2р3= =0,2048 |
5qр4= =0,4096 |
р5= =0,32768 |
Проверка: 0,00032+ 0,00064+0,0512+0,2048+0,4096+0,32768=1. Наивероятнейшее число К = 4. Ему соответствует самая большая вероятность в биномиальном распределении: 0,4096.
3.4. Непрерывная случайная величина
СПОСОБЫ ЗАДАНИЯ |
ДИФФЕРЕНЦИАЛЬНАЯ ФУНКЦИЯ f(x) |
ИНТЕГРАЛЬНАЯ ФУНКЦИЯ F(x) |
Их связь |
f(x) = F(x) |
|
Вероятностный смысл |
Плотность распределения вероятности случайной величины |
F(x) = P(X <x) Вероятность того, что значения случайной величины меньше х. |
Свойства |
1.
2.
|
0 F(X) 1 F(X) – непрерывная, неубывающая. |
|
f(x)
S=1 0 a b x |
0 a b x |
Вероятность попадания в заданный промежуток , |
|
|
Графики
(для случайной величины Х, принимающей
значения на промежутке а,
в)
3.5. Основные характеристики случайных величин
Основные характеристики, их смысл |
Вид случайной величины |
|
Дискретная |
Случайная |
|
1.Задание закона распределения |
Р(Х – хi) = Рi |
P(x<X<x+x)f(x)x |
2.Свойства вероятностей для полной группы событий |
|
|
3.Математическое ожидание (ожидаемое среднее значение). |
|
|
4.Среднее квадратическое отклонение (разбивание в единицах измерения Х) |
|
|
5.Дисперсия (рассеивание фактических значений от среднего значения а) |
|
|
6.Расчетная формула для вычисления дисперсии |
|
|
|
|
|
