
- •Тема 1. Основные понятия и теоремы
- •Основные понятия теории вероятностей
- •1.2.Система элементарных исходов
- •1.3. Классическое определение вероятности
- •1.4. Статистическое определение вероятности
- •1.5. Значения вероятности
- •1.6. Элементы комбинаторики
- •Примеры нахождения вероятности по классическому определению
- •1.7. Теоремы сложения вероятностей
- •1.8.Теоремы умножения вероятностей
- •1.9. Полная группа событий
- •1.10. Вероятность появления только одного из независимых событий
- •1.11.Вероятность появления хотя бы одного из независимых событий
- •1.12. Примеры решения задач с использованием основных теорем теории вероятностей
- •1.13. Формула полной вероятности
- •1.14. Формула Бейеса
- •Тема 2. Повторные независимые испытания
- •2.1. Формула Бернулли
- •2.1. Локальная теорема Лапласа
- •2.4. Интегральная формула Лапласа
- •2.5. Функция Лапласа ф(х)
- •2.6. Наивероятнейшее число
- •Тема 3. Случайные величины
- •3.1. Виды случайных величин
- •1. Математическое ожидание (среднее взвешенное значение случайной величины):
- •3.3. Биномиальный закон распределения
- •3.4. Непрерывная случайная величина
- •3.5. Основные характеристики случайных величин
- •3.6. Свойства математического ожидания и дисперсии
- •3.7. Непрерывные случайные величины. Примеры
2.5. Функция Лапласа ф(х)
Свойства функции:
1) Область определения: х (-; +);
2) множество значении: - 0,5 < Ф(х) < 0,5;
3) нечетность: Ф(–х) = – Ф(х);
4) строгое возрастание при х (-; +);
5) перегиб при х = 0, Ф(х) = 0;
6) при х + , Ф(х) 0,5; х – , Ф(х) – 0,5;
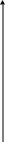 Ф(x)
Ф(x)

 0.5
0.5
 0
x
0
x
 -0.5
-0.5
Геометрически Ф(х) – площадь под кривой на промежутке [0; x] (см. приложение 1). Значения функции Ф(х) берутся по таблице (приложение 2). В таблице помещены значения х [0; +5]. Если х > 5, Ф(х) = 0,5. Для отрицательных значений Ф(–х) = – Ф(х).
2.6. Наивероятнейшее число
Наивероятнейшее число появлений события А в n независимых испытаниях - это такое число К0, которому соответствует самая большая вероятность по сравнению со всеми другими значениями К:
![]()
К
- целое число из интервала
![]() ,
где р = р(А), q
= р(
,
где р = р(А), q
= р(![]() )
для одного испытания.
)
для одного испытания.
Наивероятнейшее число может принимать либо одно, либо два значения. Если np – целое, К0 = np.
Если np – q – дробное, то К0 – единственное.
Если np – q – целое, то np + p = np + (1 – q) – целое, и наивероятнейшее число имеет два значения: К0´= np – q; К0´´= np + p.
Соответствующие вероятности им Рn(К0´) и Рn(К0´´) в этом случае равны:
Рn(К0´)= Рn(К0´´).
Вероятность, соответствующая наивероятнейшему числу, находится по формуле Бернулли (n 10), либо по локальной формуле Лапласа (n 10).
Пример. Товаровед осматривает 24 образца товаров. Вероятность того, что каждый из образцов будет признан годным к продаже, равна 0,6. Найти наивероятнейшее число образцов, которые товаровед признает годными к продаже.
Решение. По условию n = 24, p = 0,6, q = 0,4.
24*0,6 – 0,4 К0 24*0,6+0,6.
14 К0 15.
Так как np – q = 14 – целое число, то наивероятнейших чисел два: К0´= 14 и К0´´ = 15.
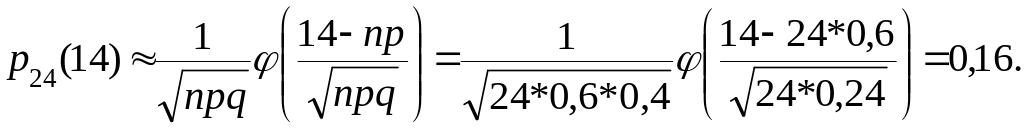
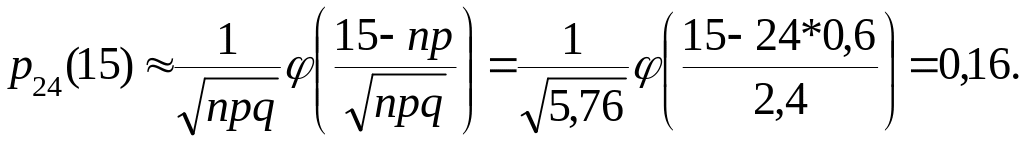
Тема 3. Случайные величины
3.1. Виды случайных величин
Случайной величиной называется переменная, принимающая свои возможные значения в зависимости от исходов испытания. Обозначается: Х,У, Z, U, V, T, …
Виды случайных величин: дискретная и непрерывная.
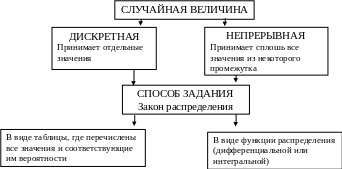
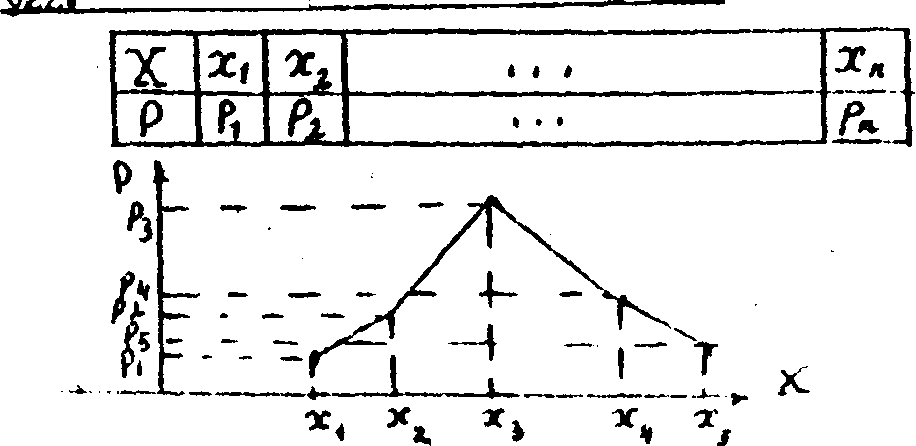
Закон распределения:
Многоугольник распределения
Основные характеристики: математическое ожидание, дисперсия, среднее квадратическое отклонение.
1. Математическое ожидание (среднее взвешенное значение случайной величины):
2. Дисперсия (рассеяние наблюдаемых
значений) Х случайной величины от
среднего значения a):
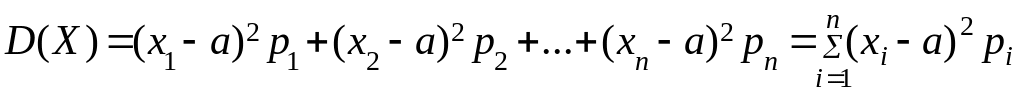
Характеризует рассеяние в квадратных единицах.
3.
Среднее
квадратическое отклонение (рассеяние
фактических значений Хi
от среднего
а,
в тех же
единицах, что и Х, в отличие от D(Х):
![]()
Расчетная формула для вычисления дисперсии:
![]() ,
,
где
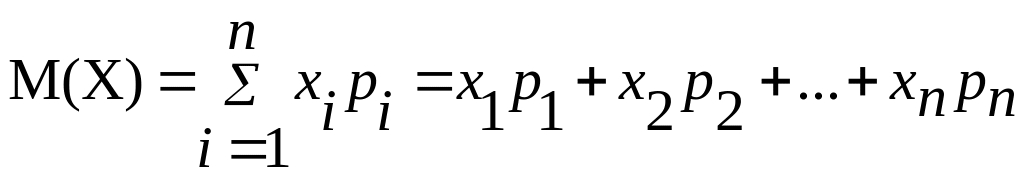 ;
;
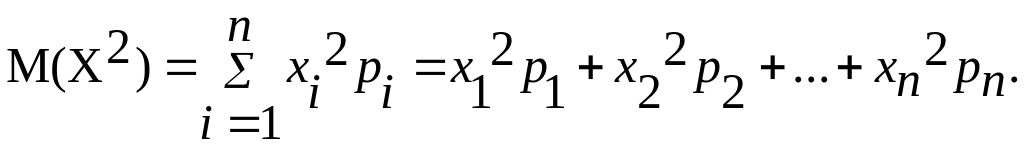
Пример. В лотерее на каждые 100 билетов разыгрываются: один выигрыш 1 млн. руб., два выигрыша по 500 тыс. руб., десять выигрышей по 100 тыс. руб., двадцать - по 10 тыс. руб. Остальные билеты не выигрывает, составить закон распределения величины выигрыша для купившего один билет и найти его основные характеристики.
Решение. Х руб. величина выигрыша одного билета.
Р(Х=1млн)=1/100; Р(Х=500 т.р.)=2/100; Р(Х=100 т.р.)=10/100;
Р(Х=10
т.р.)=20/100;
![]()
Закон распределения величины выигрыша Х:
Х |
0 |
10 т.р. |
100 т.р. |
500 т.р. |
1 млн.р. |
Р |
0,67 |
0,20 |
0,10 |
0,02 |
0,01 |
М(Х) = 0*0,67+10*020+100*0,10+500*0,02+1000*0,01=32 руб. – ожидаемый средний выигрыш на один билет.
