8. Зависимые события, условная вероятность, умножение вероятностей зависимых событий.

Если наступление одного события влияет на вероятность наступления второго события, то события называют взаимно зависимыми. Если события А и В взаимно зависимы, то условной вероятностью  называют вероятность события В, принимая, что событие А уже наступило. Условную вероятность события P(B/A) можно трактовать как вероятность события B, вычисленная при условии, что событие A произошло.

Теорема умножения вероятностей зависимых событий  где   - вероятность события B при условии, что произошло событие A.

9. Формула полной вероятности, формулы Байеса.

События образуют полную группу, если они в совокупности описывают все возможные несовместные друг с другом исходы некоторого испытания; сумма вероятностей событий полной группы равна 1. Предположим, что событие A может наступить лишь при появлении одного из несовместных событий (гипотез) H₁, H₂, ..., H_n, образующих полную группу. Тогда вероятность события A определяется как сумма произведений вероятностей каждой из гипотез на соответствующую условную вероятность события A:

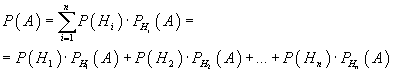
Формула Бейеса (Байеса)

Предположим, что событие A может наступить лишь при появлении одного из несовместных событий (гипотез) H₁, H₂, ..., H_n, образующих полную группу. Событие A уже произошло. Требуется вычислить условные вероятности гипотез (при условии, что событие А произошло).

10. Повторные испытания. Схема Бернулли.

Пусть проводятся независимые испытания. Далее, вероятность наступления интересующего нас события в каждом испытании постоянна и равна p. Тогда вероятность того, что рассматриваемое событие появится ровно k раз при n испытаниях (безразлично, в каком порядке), равна

В формуле Бернулли используется число сочетаний. Для реализации схемы Бернулли необходимы два условия: 1) независимость проводимых испытаний; 2) p = const (постоянное значение вероятности появления события) Наивероятнейшее число появления события (мода) при n испытаниях заключено в пределах np-q ≤ Mo ≤ np+p,

11. Формула Пуассона для повторных испытаний.

Если при наличии схемы Бернулли число испытаний n велико, а вероятность наступления события p мала, то вместо формулы Бернулли используют формулу Пуассона:

Эта формула дает удовлетворительное приближение для и . При больших рекомендуется применять формулы Лапласа (Муавра-Лапласа).локальная теорема: Если вероятность Р появления события А в каждом испытании постоянна и отлич­на от 0 и 1, то вероятность P_n(k) того, что событие A появится в n испытаниях ровно к раз приближенно =

12. Понятие случайной величины, дискретная и непрерывная случайные величины. Закон распределения вероятностей дискретной случайной величины, способы его задания.

Случайная величина - это величина, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Дискретная случайная величина принимает конечное (или счетное) число возможных значений- x_i (где i = 1.. n или i = 1 .. ∞) с определенными вероятностями. (игральные кости)

Непрерывная случайная величина может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины, независимо от величины промежутка, бесконечно. (рост человека). Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и вероятностями их появления.

Рассмотрим случайную величину X, которая принимает значения x₁, x₂, x₃ ... x_n с некоторой вероятностью p_i, где i = 1.. n. Сумма вероятностей p_i равна 1.

x1	x2	x3	...	xn
p1	p2	p3		pn

Таблица соответствия значений случайной величины и их вероятностей вида называется рядом распределения дискретной случайной величины или просто рядом распределения. Эта таблица является наиболее удобной формой задания дискретной случайной величины. Графическое представление этой таблицы называется многоугольником распределения.  По оси абсцисс откладываются возможные значения дискретной случайной величины, а по оси ординат соответствующие вероятности.