29. Параметрические критерии Стьюдента и Фишера, их сходство и различия.
Т - Критерий Стьюдента
Критерий
t Стьюдента направлен на оценку различий
величин средних 
и 
двух
выборок X и Y, которые распределены по
нормальному закону. Одним из главных
достоинств критерия является широта
его применения. Он может быть использован
для сопоставления средних у связных и
несвязных выборок, причем выборки могут
быть не равны по величине.
Случай несвязных выборок
В общем случае формула для расчета по t - критерию Стьюдента такова:
где 
Рассмотрим сначала равночисленные выборки. В этом случае n1 = n2 = n, тогда выражение (9.2) будет вычисляться следующим образом:
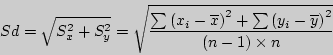
В
случае неравночисленных выборок 
,
выражение будет вычисляться следующим
образом:
В обоих случаях подсчет числа степеней свободы осуществляется по формуле:
где n1 и n2 соответственно величины первой и второй выборки.
Понятно,
что при численном равенстве выборок k
= 2 
n
- 2.
F -- критерий Фишера
Критерий
Фишера позволяет сравнивать величины
выборочных дисперсий двух рядов
наблюдений. Для вычисления 
нужно
найти отношение дисперсий двух выборок,
причем так, чтобы большая по величине
дисперсия находилась бы в числителе,
а меньшая знаменателе. Формула вычисления
по критерию Фишера F такова: 
Где 
и 
Поскольку,
согласно условию критерия, величина
числителя должна быть больше или равна
величине знаменателя, то значение
всегда
будет больше или равно единице, т.е. 
.
Число степеней свободы определяется
также просто: 
для
первой (т.е. для той выборки, величина
дисперсии которой больше) и
для
второй выборки. В таблице 18 Приложения
6 критические значения критерия
Фишера 
находятся
по величинам 
(верхняя
строчка таблицы) и 
(левый
столбец таблицы).
30. Критерий согласия χ 2- Пирсона, его особенности и процедура принятия статист. Вывода.
Критерий применяется в двух целях:
1) для сопоставления эмпирического распределения признака с теоретическим;
2) для сопоставления двух или более эмпирических распределений одного и того же признака.
Критерий построен так, что при полном совпадении эмп и теор распределений, величина х2эмп=0
Чем больше расхождения между эмп и теор распределениями, тем больше величина х2.
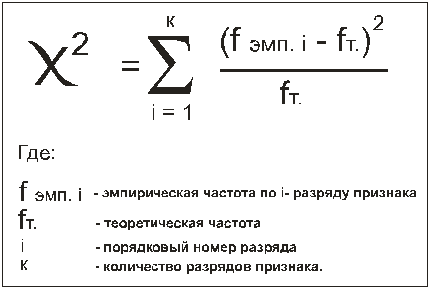
V (ню)= к – 1, где V (ню)-число степеней свободы. К – объем выборки