2.(4) Обратимые матрицы. Вычисление обратной матрицы.

Пусть дана квад-ая м-ца А порядка n . Рассм-м увад-ую м-цу n-го порядка Е=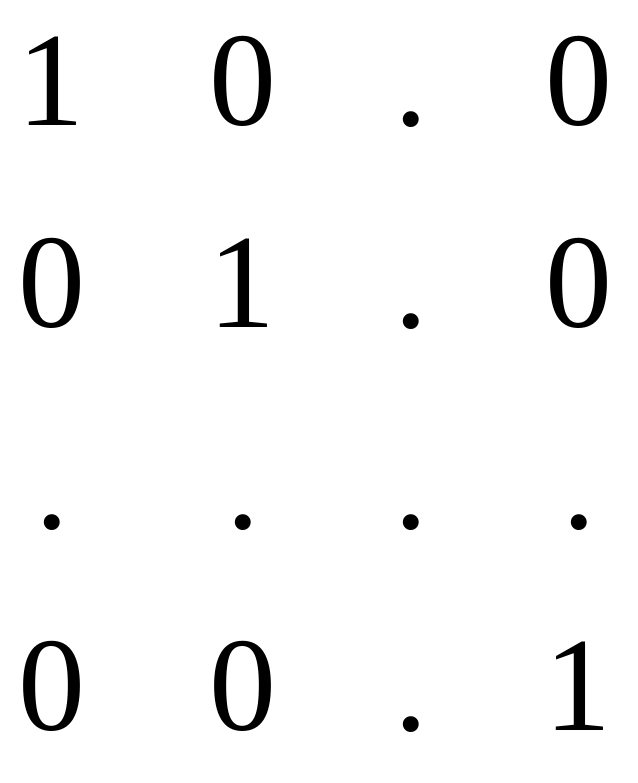 , т/да справ-во рав-во АЕ=ЕА=А (!)

Квад-ая м-ца А наз-ся обратимой, е/и существует такая м-ца В, что выпол-ся АВ=ВА=Е (*), м-ца В наз-ся обратной к м-це А

TЕОРЕМА 1: е/и м-ца А обратима, то существует лишь одна м-ца обратная к ней.

ТЕОРЕМА 2: е/и какая-либо цепочка строчечных элементарных преобразований переводит квад-ую м-цу А в единичеую м-цу Е, то м-ца А обратима и эта же цепочка строчечных элементарных преобразований переводит м-цу Е в м-цу А^-1 .

ПРАВИЛО НАХОЖДЕНИЯ ОБРАТНОЙ М-ЦЫ: надо составить м-цу ||А|Е|| размерности n*2n и путем цепочки элемен-ных преобр-ий привести ее к м-це

||Е|С||. М-ца С и будет А^-1 .

ПРИМЕР:А=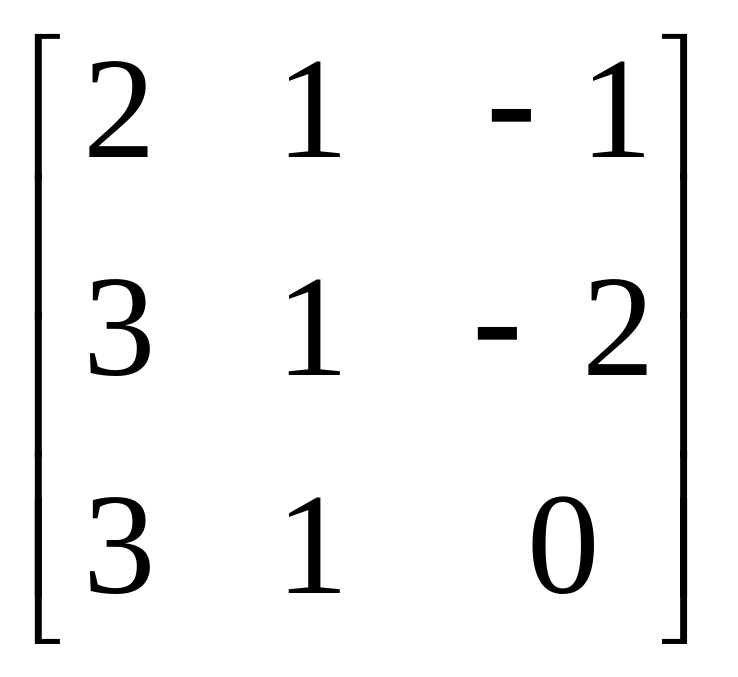

~ ~ ~ ~ ~ ~ .

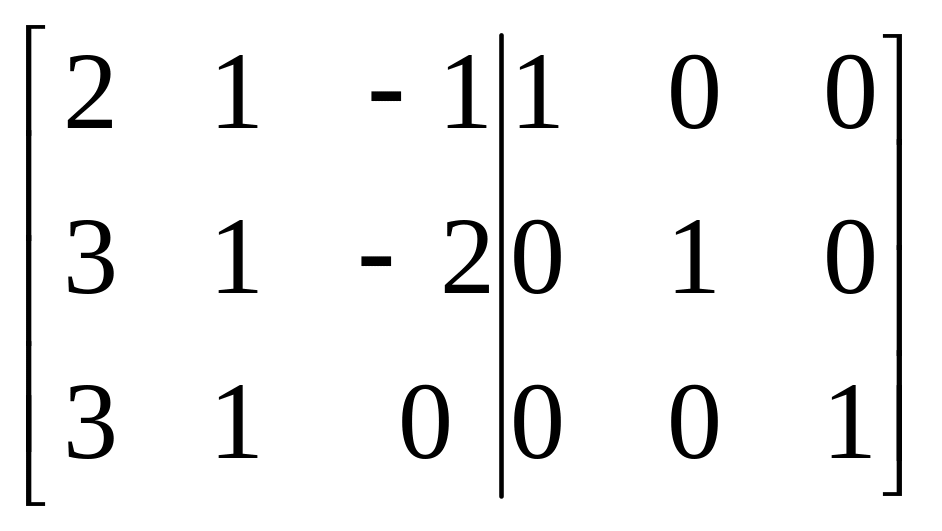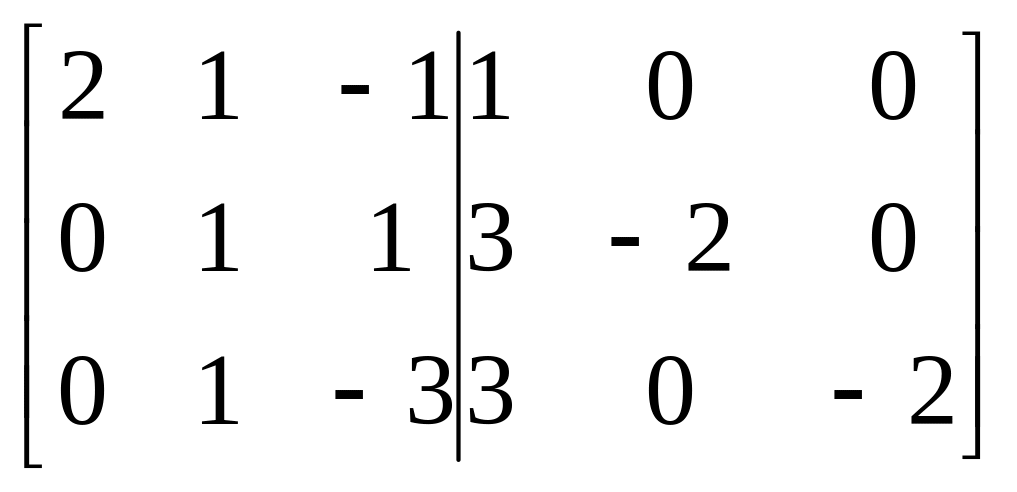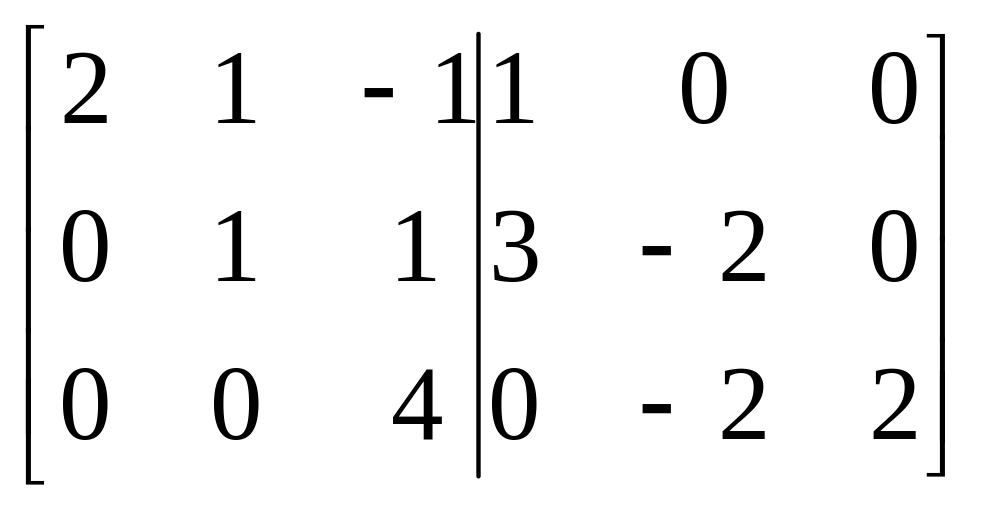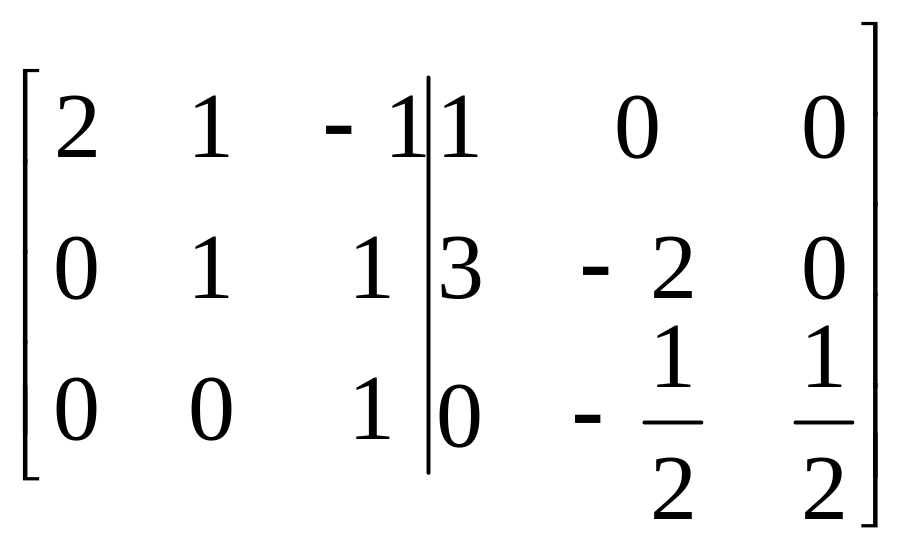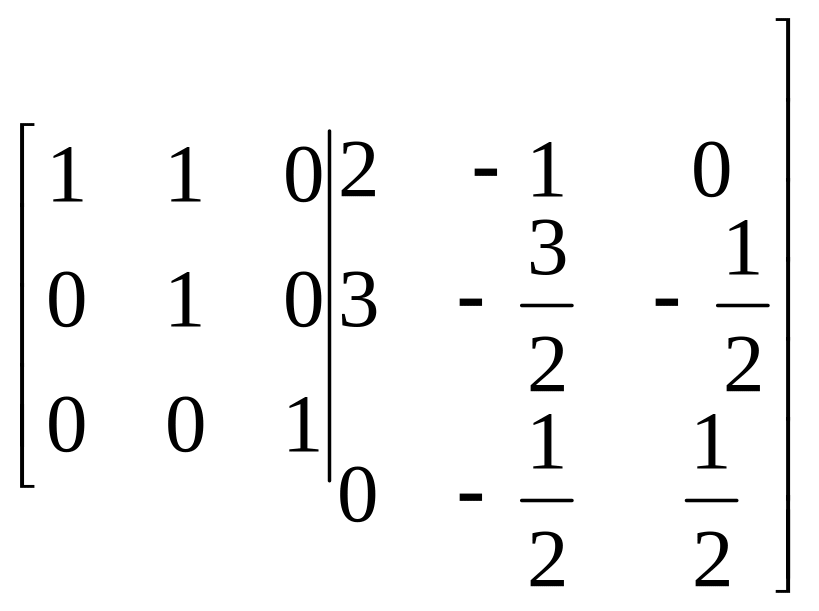А^-1 =

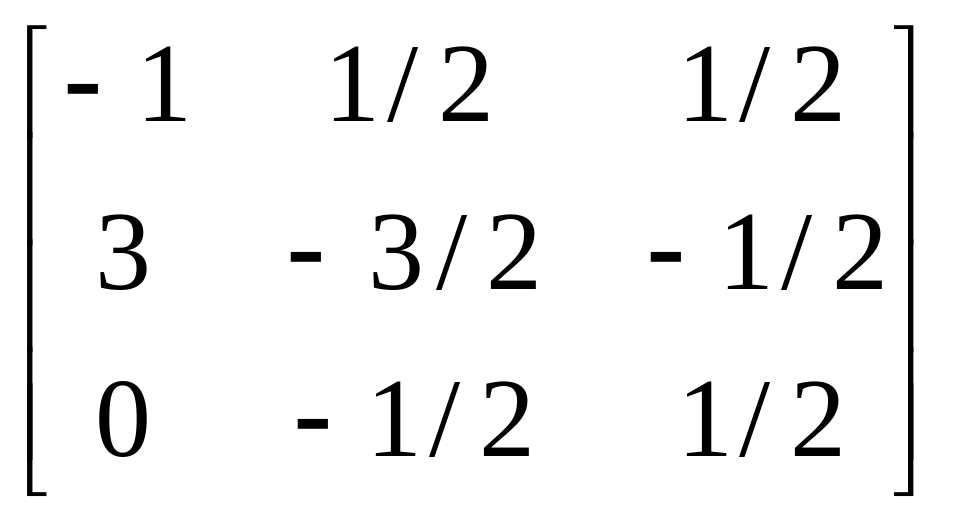
Чтобы проверить А*А^-1 =Е

ФОРМУЛА ОБРАТНОЙ МАТРИЦЫ: пусть дана квад-ая м-ца порядка n А=||а_ij||.Предположим она явл-ся обратимой. Ч/з А_ij обоз-м алгебр-ое дополнение для эл-та а_ij м-цы А . Определим м-цу

А^{* def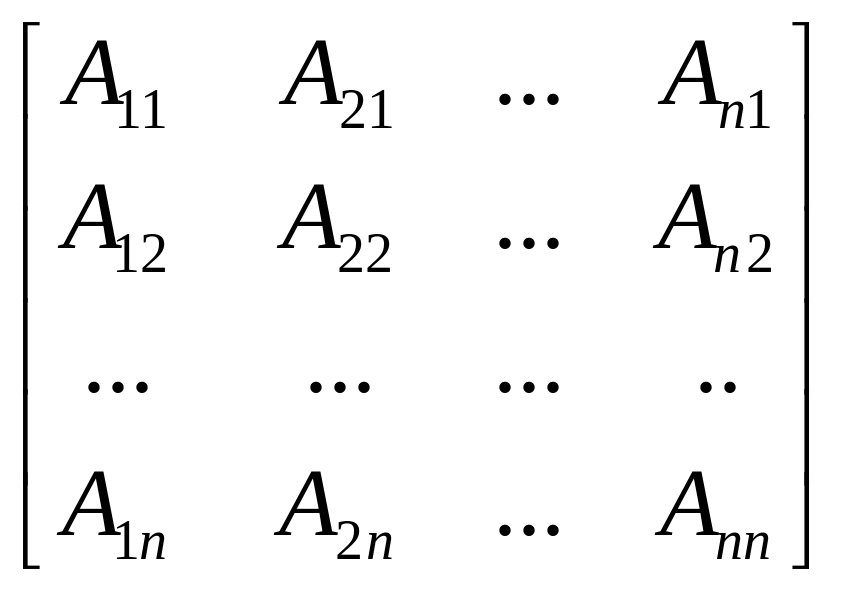}= она состоит из алгебр-ких дополнений м-цы А. Определенная таким образом м-ца А^* наз-ся присоединенной для м-цы А.

ТЕОРЕМА 3: е/и det A 0, то м-ца обратима и

ПРИМЕР: А=

А₁₁=(-1)¹⁺¹ =7^, А₂₁=(-1)²⁺¹ =-21 А₃₁=(-1)³⁺¹ =14

А₁₂=(-1)¹⁺² =4 А₂₂=(-1)²⁺² =-12 А₃₂=(-1)³⁺² =7

А₁₃=(-1)¹⁺³ =-1 А₂₃=(-1)²⁺³ =10 А₃₃=(-1)³⁺³ =-7

А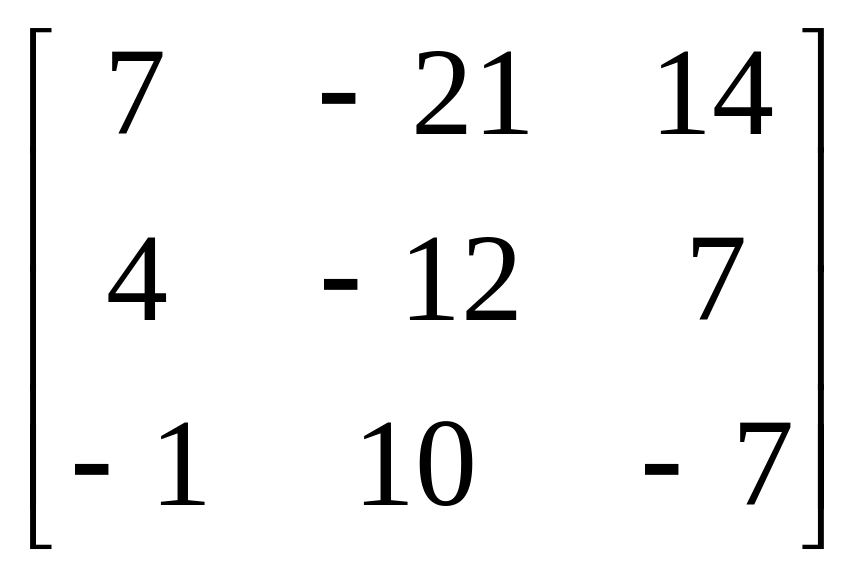^*= |А|=-4-63+60+0+14=7

А^-1=1/7 =

3.(18).Методика введения понятия первообразной.Площадь криволинейной трапеции.

Первообразная и интеграл (18).

Первообразная. Первообразные степенной функции с целым показателем (п не равен -1), синуса и косинуса. Простейшие правила нахождения первообразных. Площадь криволинейной трапеции. Интеграл. Формула Ньютона-Лейбница. Применение интеграла к вычислению площадей и объемов.

Основная цель - познакомить учащихся с интегрированием как операцией, обратной дифференцированию; показать применение интеграла к решению геометрических задач. Задача обработки навыков нахождения первообразных не ставится, упражнения сводятся к простому применению таблиц и правил нахождения первообразных. Интеграл вводится на основе рассмотрения задачи о площади криволинейной трапеции и построения интегральных сумм. Формула Ньютона-Лейбница вводится на основе наглядных представлений. В качестве иллюстрации применения интеграла рассматриваются только задачи о вычислении площадей и объемов. Следует учесть, чтo формула объема шара выводится при изучении данной темы и исполъзуется затем в курсе геометрий.

Материал учебника, касающийся работы переменной силы и нахождения центра масс, не является обязательным. При изучении темы целесообразно широко применять графические иллюстрации.

Методика введения понятия интеграла. Приложения интеграла

Опорные знания: Первообразная основ-ые св-ва первообразных Площадь кривол-ой трапеции.

Повторение с помощью математи-го диктанта с взаимной проверкой. Понятие интеграла вводится ка другой подход к задаче вычисления площади криволинейной трапеции. Решая з-чи на вычисления площади крив. трапеции нетрудно убедиться что площадь полностью определяется ф-ей f(х) и концами промежутков А и В. Действительно всякая первооб-ная F(x) для фун-и f(x) отл-ся от любой другой ее первообразной F(x) на пост-ую, поэтому Ф(х)=F(x)+c ,т.е. Ф(в)-Ф(а)=(F(b)+c)-(F(a)+c)=F(b)-F(a) – т. о. любые две первообразные для ф-ии f(x) имеют на отрезке [А,В] одно и тоже приращение. Приращение первообразной для ф-ии f(x) на [А,В] и обознач-ся . По опр-нию , где F(x)=f(x). С начало предлагаем польз-я для peшe-я зад-ч на вычисление площадей формулой, выр-ей площадь как разность знач-ии первообразной. При док-ве темы, что площадь кривол трапеции не зависит от того какой из первообразных данной ф-ии восп-ся для выч-ия площади полезно проделать в решенных перед этим задачах вычис-ия исп-ия различных первообразных для одной и той же функции.

Усложнения

1) Ф-ия f(x) зад-ся а пределы инте-ия надо найти из условия задачи.(Например выч-ть площадь фигуры ограниченной параболой и осью абсцисс, если парабола пересекается с осью абсцисс) 2) Задаются две ф-и, графики которых имеют пересечения и пределы интег-ия крив. трапеции приходится разбирать части. 3)Заданы 2 ф-ии но пределы интегр-ия приход-ся наход-ть в процессе решения задачи.

Приложения интеграла. А т

Опр Пусть на [а,b] оси Ох задана непрерывная, ф-ия(знак не меняется). Фиг-ру ограниченную графиком этой ф-ии, отрезком [а,b] прямыми х=а и х=b называют криволинейной трап-ей.

Тh. Если f непрерывна неотрицат на [а,b] ф-ия, и сушест-ет ее первообразная на этом отрезке, то площадь соответ-ей трапеции = приращению первой на [а,b] (1).

S=F(b)-F(a), f-непрер. и неотр на [а,b]. разобьем [а,b] на n отрез. одинак-ой длины т. х₀=а<х1<…< <x_n=b и пусть х=(b-а)/n=

=х_k-x_к-1, k=1..n. На каждом из отрезков [x_k-1,x_k] как на основании построим прямоугольник высотой f(x_k-1) площадь этого прямоугольника =f(x_k-1)*x=(b-a)/n*f(x_k-1) =

= A  площадей всех таких прямоугольников =Sl=(b-a)/n[f(x₀)+…+f(x_n-1)]. В силу непр-ти f обья-ия простран-ых прямоуг-ов при n (х0) почти совп-ет с криволин. трап. S_nS при n. Для любых непрерывных на [а,b] функ-ии f. S_n при n стремиться к некоторому числу то число наз-ся (по опр) интегралом фун-и f от а до b и обоз-ют , т.е. S_n при n, а и b пределы интегрирования. F-подинтегральная ф-ия, х- переменная интегрирования. Если f(x) 0 на [а,b], то S_n= (2) Функ-ия, напр-р, Из (1),(2)  =F(b)-F(a) непрерывна на [а,b].