Билет №19

1.(20) . Плоскость Лобачевского. Непротиворечивость системы аксиом плоскости Лобачевского. Взаимное расположение прямых на плоскости Лобачевского.

Геометрия Лобачевского основана на аксиомах групп I-IV абсолютной геометрии и на аксиоме Лобачевского V^*.

Группа I. Аксиомы принадлежности.

Аксиомы этой группы определяют свойства взаимного располо­жения точек, прямых и плоскостей, выражаемые словом «принадлежит» (или «лежит на», «проходит через»). Группа I содержит следующие восемь аксиом.

1⁰. Для любых двух точек А, В, существует прямая а, проходящая через эти точки.

2⁰. Для любых двух точек А, В, существует не более одной прямой, проходящей через эти точки.

3⁰. Любая прямая содержит по крайней мере две точки. Сущест­вуют по крайней мере три точки, не лежащие на одной прямой.

4⁰. Для любых трех точек А, В, С, не лежащих на одной прямой, существует плоскость, проходящая через эти точки. На каждой плоскости лежит хотя бы одна точка.

5⁰. Для любых трех точек, не лежащих на одной прямой, существует не более одной плоскости, проходящей через эти точки.

6⁰. Если две точки A и В прямой а лежат в плоскости , то каждая точка прямой а лежит в плоскости .

Группа II. Аксиомы порядка.

1⁰. Для любых точек А, В, С , лежащих на одной прямой, если В лежит между А и С, то А, В, С различны и В лежит между С и А.

2⁰. Для любых точек А, В существует точка С, лежащая на прямой АВ такая, что В лежит между А и С.

3⁰. Среди любых трех точек прямой существует не более одной точки, лежащей между двумя другими.

4⁰(аксиома Паша). Пусть А, В, С – три точки, не лежащие на одной прямой, а – прямая в плоскости АВС, не проходящая ни через одну из точек А, В, С. Тогда если прямая а проходит через точку отрезка АВ, то она проходит также через точку отрезка АС или ВС.

Группа III. Аксиомы равенства.

1⁰. Если даны отрезок АВ и луч, исходящий из точки А', то существует точка В', принадлежащая данному лучу, такая, что АВ = А'В'.

2⁰. Если А'В' = АВ и А"В" = АВ, то А'В' = А"В".

3⁰. Пусть итмеется 2 отрезка АВ и ВС, не имеющих общих внутренних точек. Если АВ = А'В' и ВС = В'С, причем т. лежит между , то .

4⁰. Пусть А, В, С — три точки, не. лежащие на одной прямой, и А', В', — тоже три точки, не лежащие на одной прямой. Если при этом АВ=А'В', АС = А'С, , то .

Группа IV. Аксиомы непрерывности.

1⁰. (аксиома Архимеда). Для любых двух отрезков АВ и CD существует такое натуральное число n, что .

2⁰. (аксиома Кантора). Пусть на произвольной прямой а дана бесконечная последовательность отрезков, из которых каждый последующий лежит внутри предыдущего и, кроме того, для любого отрезка CD найдется натуральное число п, такое, что А_пВ_п < CD. Тогда на прямой а существует точка М, принадлежащая каждому из отрезков данной последовательности.

Аксиоме Лобачевского:

V*. Пусть а — произвольная прямая и А — точка, не лежащая на этой прямой. Тогда в плоскости, определяемой точкой А и прямой а, существует не менее двух прямых, проходящих через точ­ку А и не пересекающих прямую а.

Плоскость Лобачевского в модели Клейна изо­бражается в виде внутренности круга, причем прямые изобража­ются хордами. Пересекающиеся прямые изображаются пересе­кающимися хордами. Если общая точка будет стремиться по одной из прямых к бесконечности, то параллельные прямые будут изображаться хордами, общая точка которых принадле­жит абсолюту (ограничивающей внутренность круга окружности). Сверхпараллельные прямые в моде­ли изображаются хордами, которые будучи продолжены пере­секутся в точке, принадлежащей внешней области абсолюта.

П учок прямых I рода при дан­ном отображении переходит в совокупность хорд, пересекающихся в общей точке, принадлежащей внутренности абсолюта (рис. 1). Пучок прямых II рода, т.е. прямых, параллельных друг другу в данном направлении, переходит в совокупность хорд, пе­ресекающихся в некоторой точке абсолюта (рис. 2). Пучок прямых III рода отображается в совокупность хорд, пересекающихся в некоторой точке вне абсолюта (рис. 4). Точ­ки абсолюта называются бесконечно удаленными точками и точки вне абсолюта — идеальными точками плоскости Лобачевского. Поэтому пучки прямых II и III родов наз. иногда пучками с бесконечно удаленными или соот­ветственно идеальными центрами.

Ось пучка прямых III рода явл. полярой полюса – своего идеального центра. В самом деле, допустим, что ось пучка не является полярой идеального центра.

Предположим, например, что она не проходит через точку (рис. 4) пересечения поляры точки Р с абсолютом. Тогда на плоскости Лобачевского будет существовать прямая СС₁, одновременно перпендикулярная и параллельная к прямой СВ, что невозможно.

Перенося по отображению во внутренность абсолюта основ­ные понятия отображаемой плоскости Лобачевского, в ито­ге получим модель Клейна.

Параллельные прямые на плоскости Лоб-го. Пр.АВ наз. параллельнойпр.СD, если эти прямые не имеют общих точек и, каковы бы ни были точки P и Q, лежащие соответственно на прямых АВ и CD, любой внутренний луч угла QPB пересекает луч QD (рис.).

Д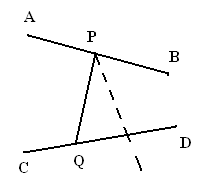 ве прямые на плоскости Лобачевского наз. расходящимися (или сверхпараллельными), если они не пересекаются и не параллельны.