БИЛЕТ №24

1.(6).Числовые ряды. Признаки сходимости: Даламбера и итегральный. Абс и условно сходящ ряды.

Числовой ряд. Общий член ряда

Пусть задана бесконечная последовательность чисел а1, а2, а3, ... Рассмотрим выражение а1+а2+а3+… представляющее собой «сумму бесконечного множества слагаемых». Оно называется числовым рядом, а сами числа а1, а2, а3, ... — членами ряда.

Член ряда аn с произвольным (неопределенным) номером n называется общим членом. Ясно, что аn есть некоторая функция от n. Эту функцию необходимо указать, так как иначе нельзя считать заданной саму последовательность а1, а2, а3, ... Однако чаще всего выражение для общего члена ряда (как функции от n) не указывают отдельно, а вносят в ряд и пишут а1+а2+а3+...+аn+...

Теорема 4 (признак сходимости Даламбера).

Если для ряда al+a2+...+an+... с положительными членами существует такое число q < 1, что при всех n (или хотя бы начиная с некоторого n) выполняется неравенство an+1/an=<q (число q одно и то же для всех n), то ряд сходится. Если же an+1/an>=1 (для всех n или начиная с некоторого n), то ряд расходится.

Отбросив, если нужно, несколько первых членов ряда (что не влияет на сходимость), можно считать, что неравенство выполняется для всех n = 1, 2,.... Перепишем это неравенство в виде an+l=<qan. Отсюда имеем: a2=<qa1, а3=<qa2=<q²a1 и т.д.; вообще, при любом n справедливо нера­венство an<q^n-1a1

Это показывает, что члены ряда a1+a2+...+an+... не превосходят соответствующих членов бесконечной геометрической прогрессии a1+qal+q²a1+...+q^n-1+... Поскольку 0=<q<1, эта прогрессия является сходящейся. Отсюда в силу первого признака сравнения вытекает сходимость ряда a1+a2+...+an+...

В том случае, если an+1/an>1, имеем аn+1>аn, т.е. члены данного ряда возрас­тают. Тем самым нарушен необходимый признак сходимости (lima#0) и, следо­вательно, ряд расходится.

Теорема 6 (интегральный признак сходимости).

Пусть функция f(x) определена для х>0, положительна, монотонно убывает и стремится к нулю при х->00. Тогда для сходимости ряда f(1)+f(2)+…(13) необходимо и достаточно, чтобы сходился несобственный интеграл 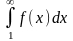(14) Сходимость интеграла (14) означает существование предела при n->00 интеграла

(15) а, значит, сходимость ряда 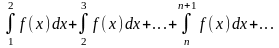(16) для которого интеграл (15) является частичной суммой (если сложить первые n-1 членов ряда, то получим интеграл

(15)). Поэтому задача состоит в том, чтобы доказать одновременную сходимость или расходимость рядов (13) и (16).

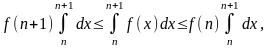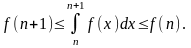В силу монотонности f(x) на любом отрезке [n,n+1] имеем f(n+1)=<f(x)=<f(n), (n=1, 2,...). Интегрируя по отрезку [n, n+1], получим т.е. (17)

Если сходится ряд (13), то из второго неравенства в (17) согласно признаку сравнения вытекает сходимость ряда (16). Обратно, если сходится ряд (16), то из первого неравенства в (17) согласно признаку сравнения вытекает сходимость ряди f(2)+f(З)+...+f(n+1)+..., а, значит, и ряда (13).

Абсолютно сходящиеся ряды

Пусть дан знакопеременный ряд. Рассмотрим ряд

|a1|+|a2|+…+|an|+… (8) членами которого являются модули членов ряда. Очевидно, что (8) есть ряд с положительными членами.

Определение 1.

Ряд называется абсолютно сходящимся, если сходится ряд (8), составленный из модулей его членов.

Теорема 2.

Всякий абсолютно сходящийся ряд сходится. Сумма такого ряда равна разности между суммой его плюс-ряда и суммой минус-ряда.

Пусть ряд абсолютно сходится, т.е. сходится ряд (8). Обозначим час­тичные суммы ряда (8) через A*n. Имеем

A*n=A+n1+A-n2. (9)

Ввиду сходимости ряда (8) его частичные суммы A*n ограничены сверху некото­рым числом С. Тогда из равенства (9) следует A+n1<С и A-n2<С, т.е. частичные суммы плюс- и минус-ряда также ограничены сверху числом С. Согласно крите­рию сходимости рядов с положительными членами отсюда вытекает сходимость плюс- и минус-рядов, т.е. существование чисел А+ =limА+k и А- =limA-l, k,l->00. Если

теперь перейти к пределу при n->00, то получим limAn=А+-А-, n->00. Принимая во внимание теорему 2, можно сказать, что абсолютно сходящий­ся ряд - это ряд, который не только сходится сам, но и обладает сходящимся рядом из модулей своих членов.

4. Условно сходящиеся ряды

Определение 2. Ряд а1+а2+...+аn+... называется условно сходящимся, если он сходится, но в то же время ряд из модулей |а1|+|а2|+...+|an|+... расходится. Таким образом, все сходящиеся ряды можно разделить на два класса: абсолютно сходящиеся, т.е. такие, для которых ряд из модулей их членов сходится и условно сходящиеся, для которых ряд из модулей членов расходится.