23. Дискретизация сигнала по времени.

Последовательность основных операций преобразования, производимых над сигналом в ЦСП м. б. описана такой схемой:

Г де блок 1 – дискретизатор, 2 – квантующее устройство, 3 – кодер, 4 – канал передачи, 5 – декодер, 6 – блок восстановления непрерывного сигнала.

Осциллограммы показаны на рисунке 2:

Д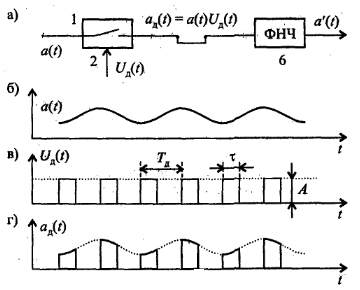 искретизатор 1 построен по схеме перемножителя исходного сигнала a(t) с некоторой импульсной последовательностью 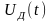. Дискретизированный по времени сигнал 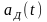показан на рисунке – г). Блок восстановления 6 показывает преобразование дискретного сигнала в непрерывный 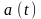, который должен мало отличаться от исходного 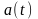. Определим параметры блоков 1 и 6, при которых это условие выполняется.

Полагаем, что представляет собой периодич. послед-ть с постоянными параметрами: амплитудой А, длительностью τ и периодом 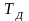. Тогда Ud(t) выразим: 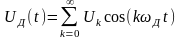. Дискретизированный сигнал равен: 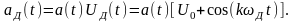Если полагать известным спектр входного сигнала, то применяя преобразование Фурье к , получаем спектр дискретизированного сигнала 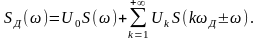Т.е. в виде суммы спектра исходного сигнала с «весом» U0 и пары боковых спектров относительно k-й гармоники частоты дискретизации с «весом» Uk; k=1,2…

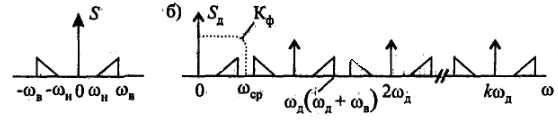
При идеальной дискретизации сигнала последовательностью δ – импульсов получим: .

П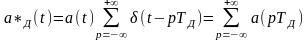 ропустив дискретизированный сигнал через ФНЧ, можно выделить без искажений спектр исходного сигнала, т.е. осуществить безискаженное восстановление аналогового непрерывного сигнала по последовательности его дискретных отсчетов.

На практике для дальнейших преобразований используется не последовательность идеальных выборок, а сигнал 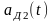, где каждая выборка запоминается на время τ. Сигнал такого вида называется амплитудно-импульсной модуляцией 2-го рода (АИМ-2). Сигнал АИМ-2 можно представить как результат свертки сигнала 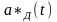с одиночным прямоугольным импульсом 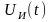. Спектр сигнала АИМ-2 имеет частотные искажения, для устранения которых после ФНЧ включают частотный корректор.

24. Квантование сигнала. Алгоритмы квантования

Д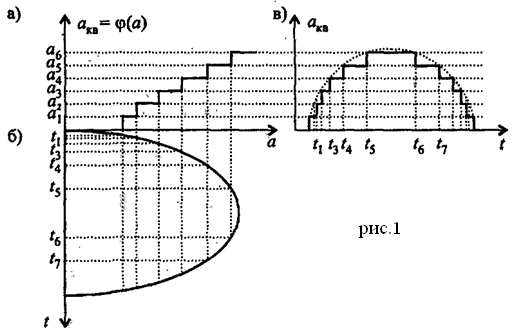 искретизация по уровню(квантование по уровню) обеспечивает переход от множества возможных значений, которые может принимать сигнал, к ограниченному. Такой переход обеспечивает нелинейное устройство – квантователь. При передачи однополярных сигналов, динамическая характеристика квантователя имеет вид как на рисунке 1а. При изменении входного сигнала а(t) в интервале времени t1+t7 (рис. 1б) он примет бесконечное число возможных значений. Сигнал 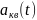на выходе квантователя может принимать только дискретное множество разрешенных значений(рис. 1в). Т.е. чем больше число разрешенных уровней 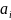и меньше шаг квантования 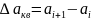, тем меньше отличается квантованный сигнал от исходного а(t).

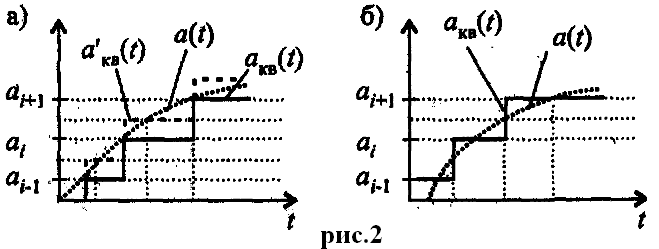
Возможны два варианта алгоритма квантования. Для первого применяется правило: 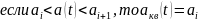(рис. 2а). Для второго: 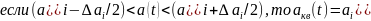. Величина 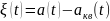называется ошибкой квантования. Для второго алгоритма ошибка квантования меньше, поэтому он предпочтительнее. С точки зрения технической реализации первый алгоритм проще.

В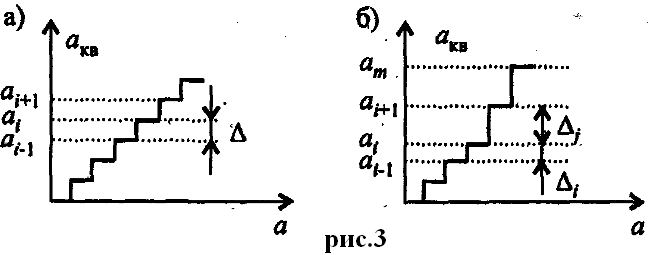 зависимости от выбора уровней и интервалов квантования бывают квантователи с равномерной(рис. 3а) и неравномерной(рис. 3б) шкалой квантования. В первом случае интервал квантования между соседними уровнями всегда одинаков, во втором случае он различен. Использование квантующей характеристики всегда приводит к искажениям сигнала на выходе системы. Это неустранимые искажения.