21.02.2012 Логический элемент или.Логическое сложение. Дизъюнкция
Лампа на выходе схемы будет гореть , если какой либо из ключей или оба сразу окажутся замкнутыми. Не будет гореть ,если оба ключа разомкнуты.
Булево выражение y=x1+x2
Символ ИЛИ + \\ Символ ИЛИ V Читается: y= x1 ИЛИ x2
Логическое отрицание. Логический элемент НЕ. Инверсия.
В схеме “НЕ” часто называемой инвертором есть только один вход и один выход.
Основная функция схемы “НЕ” состоит в том, чтобы обеспечивать на выходе сигнал, противоположный сигналу на входе.
Инвектор дополняет или инвертирует(отрицает) входной сигнал.
Булево выражение: у=Х Читается: у= НЕ х
В Булевом выраении для лог.функции “НЕ” черта над обозначением входного сигнала указывает на то ,что входной сигнал инвертирован.
При прохождении сигнала через инвектор сигнал инвертируется, или дополняется или отрицается. Инвертируется, или дополняется или отрицается это одно и тоже. Бывают схемы, когда входной сигнал Х проходит через 2 инвектора , этот сигнал сначала инвертируется и получается сигнал Х , а затем сигнал инвертируется вторично и получается сигнал двойное не Х ( Х с двумя чертами ).
Лог. 1 на входе инвертированая дважды даёт исходную двоичную единицу на выходе. Таким образом Х с двумя чертами = Х.
Двойное инвертирование какого либо сигнала не меняет его первоначального значения.
28.02.2012 Свойства конъюнкции, дизъюнкции, инверсии
Для сложного логического выражения установлен определённый порядок выполнения операций: 1) Операция инверсии (отрицание) 2) Операция конъюнкции (умножение) 3) Операция дизъюнкции (сложение)
Например:
Х1
+
Х2
* Х3
+ Х4
* Х2
Первое действие – черта (инверсия) Х3 и Х4 Второе действие умножение Третье действие сложение
Если требуется изменить порядок действий, то ставим скобки!
(Х1 + Х2) * (Х3 + Х4) * Х2
Булева алгебра была развита Джоржем Булем (1815-1864)
Она применятся для анализа цифровых лог. схем, она является основой всех преобразований , которые используются для упрощения логических выражений.
С помощью законов алгебры-логики преобразуют и превращают исходные лог.функции.
В алгебре-логики используют переместительный, сочитательный, распределительный, инверсии законы.
Кр законы и функции Переместительный закон
Графически переместительный закон
Сочитательный закон
Графически лог.сложение:
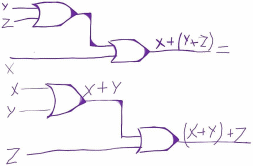
Графически
лог. умножение:
Распределительный закон
Графически лог.сложение
Графическое логическое умножение
06.03.2012
Закон инверсии (Правило Де Моргана) Инверсия любого сложного выражения в котором аргументы, либо их инверсии связаны между собой операциями конъюнкции и дизъюнкции, может быть представлена тем же выражением без инверсии с изменением всех знаков конъюнкции на знаки дизъюнксии и наоборот дизъюнкция на конъюнкцию и с инверсией всех аргументов.
Из
правила Де Моргана следует закон двойного
отрицания.
Х = Х
Используя основные законы алгебры-логики, а также свойства логических функций И,ИЛИ,НЕ можно вывести следующие заключения: 1) А + 1 = 1
2) А+0 = А
3) А * 0 = 0
4) А * 1 = 1
5) А + А = А
6)
А + А = 1
7) A * A = A
Fotka v samsunge
8) A * A = 0
Fotka v samsunge
9)A=A
Fotka v samsunge
10) А + АВ = А А ( 1+ +В ) = А*1 =А
27 страница конспекта pdf
05.04.2012 Примеры:
Выражение элементарных функций через операции И, ИЛИ , НЕ
1.Операция запрета Булево выражение Х1 ∆ Х2 = Х1 * Х2 Читается: Х1 даёт запрет по Х2 ; Х1 , НО НЕ Х2
Х1 |
Х2 |
Не Х2 |
Х1*не Х2 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |