Решение.
а) Анализ данных и формул.
Рассмотрим адиабатное истечение газа через суживающееся сопло из резервуара достаточно большого объема, в котором изменением давления можно пренебречь (p1 = const) (рис.3).
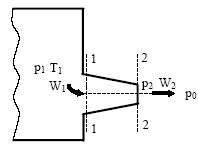
Рис. 3. Истечение газа из резервуара
В резервуаре газ имеет
параметры
,
,
,
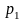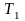а на выходе из сопла
,
,
,
.
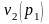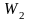Давление среды, в которую происходит
истечение газа, обозначим
.
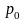Основной характеристикой процесса
истечения является отношение конечного
давления к начальному, т. е. величина
.
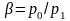В зависимости от отношения
давлений можно выделить три характерных
режима истечения газа: при
− докритический, при
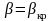− критический и при
−
сверхкритический режимы.
Значение
,
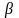при котором расход газа достигает
максимума, называется критическим
,
и находится по формуле:
При критическом режиме
также происходит полное расширение
газа в пределах сопла, на срезе сопла
,
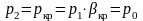скорость на выходе равна критической
скорости – скорости звука (рис. 2, б),
располагаемая работа полностью
расходуется на увеличение кинетической
энергии газа.
Рис. 4. Процесс истечения газа в pv – координатах и характер изменения скорости звука и скорости истечения газа при .
Скорость газа на выходе из
суживающегося сопла определяется по
формуле:
б) Вычисления.
Для двухатомного газа k = 1,4 критическое отношение давлений
Рассчитаем отношение давлений
Сравниваем полученное отношение с критическим значением и устанавливаем, что скорость истечения будет критической
Ответ: давление среды равно атмосферному 101,3 кПа, а скорость истечения: 313,345 м/с.
7.Через противопожарную стену проходит стальной стержень, боковая поверхность которого тщательно теплоизолирована, т.е. стержень представляет собой полуограниченное тело. Торец стержня нагревается до температуры 900°С, которая затем остается постоянной. Начальная температура стержня 20°С. Определить температуру стержня на выходе из стены толщиной 25 см в смежное помещение через 15 мин.
Дано: сталь Т=900°С=const; T0=20°С τ=15 мин d=25 см |
СИ: a=0,04·10-4 м2/с – температуропроводность стали Т0=20°С=20+273,15=293,15 К Т=900°С=900+273,15=1173,15 К τ =15 мин=9·103 с d=25 см =0,25 м
|
Найти: Tвых- ? |
Решение.
а) Анализ данных и формул.
Полуограниченным можно назвать достаточно большое тело с одной плоской поверхностью, к которой подводится теплота и боковой поверхностью, которая тщательно теплоизолирована.
Температура такого тела обычно меняется только по оси х, поэтому уравнение теплопроводности будет одномерным.
Дифференциальное уравнение теплопроводности Фурье:
,
где
с и ρ
– соответственно удельная теплоёмкость
и плотность вещества;
– коэффициент температуропроводимости;
– оператор Лапласа.
Одномерное уравнение теплопроводности:
(1)
Начальное распределение температур будем считать равномерным:
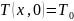
Условия полуограниченности задают температуру и плотность теплового потока при х→∞:
Введем граничные условия на поверхности x=0:
В нашем случае температура поверхности стержня при x=0 резко нагревается до температуры Т и поддерживается постоянной - это граничные условия 1-го рода.
Тогда решение одномерного уравнения теплопроводности (1) получим в виде:
(2)
где
- число Фурье; (3)
– коэффициент температуропроводности;
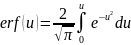– функция ошибок Гаусса.
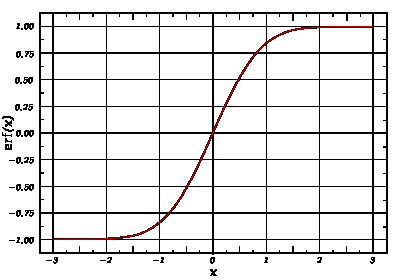
Рис. 5. График функции ошибок.
б) Вычисления.
Из формулы (2) выразим Твых:
(4)
Используя формулу (3) определим число Фурье при х=d:
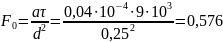
Определим значение аргумента функции ошибок при х=d:
По рисунку 5, а если точнее то по таблице в справочной литературе определим значение функции erf(x)=0,113.
Сейчас можно определить значение искомой температуры формула (4):
Ответ: температура на другом конце стержня равна 800°С
8. Определить безопасное расстояние от поверхности факела горящего штабеля древесины до соседнего штабеля, если площадь поверхности факела 12×6 м, его степень черноты 0,7, а средняя температура 1027°С. Температура воспламенения древесины 250°С, степень черноты древесины 0,9. Критическая плотность потока qкр=12800 Вт/м2.
Дано: S=12x6 м ε1=0,7 ε2=0,9 T1=1027°С T2=250°С qкр=12800 Вт/м2 |
СИ: a=0,04·10-4 м2/с – температуропроводность стали Т1=1027°С=1027+273,15=1300,15 К Т2=250°С=250+273,15=523,15 К S=12x6 =72м2
|
Найти: Tвых- ? |