2. Проектирование и исследование зубчатого механизма

2.1.Структурный анализ зубчатого механизма

Прямозубое цилиндрическое колесо:

d_α – диаметр вершин;

d_f – диаметр впадин;

d – делительный диаметр.

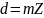, где 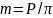- модуль зубчатого колеса, Р – окружной шаг зубьев.

Делительная окружность является базовой для определения элементов зубьев и их размеров.

h_α – делительная высота головки зуба;

h_f – делительная высота ножки зуба.

- угловой шаг зубьев.

Эволютой называется геометрическое место центров кривизны какой-либо кривой, а сама кривая по отношению к эволюте называется эвольвентой (разверткой). Следовательно, эвольвента окружности, которая была предложена для образования профилей зубьев в 1727 г. Л. Эйлером, есть кривая, эволюта которой окружность, называемая основной.

Если профили зубьев двух колес очерчены по эвольвентам, то точка их касания лежит на общей касательной к основным окружностям, являющейся общей нормалью к обеим эвольвентам в точке их касания. Так как нормаль к эвольвентам в любой точке их касания всегда проходит через одну и ту же точку Р (полюс зацепления) на межосевой линии О₁О₂, то эвольвентное зацепление обеспечивает постоянство передаточного отношения. Касание эвольвент возможно лишь на отрезке АВ, называемом линией зацепления. За пределами АВ происходит пересечение эвольвент, а для зубьев – интерференция, при нарезании же – подрезание зубьев у ножки.

Так как не вся эвольвента используется для образования боковых профилей зубьев, то действительное зацепление пары зубьев будет происходить на отрезке 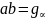, называемом активной линией зацепления. Она ограничена окружностями вершин зубчатых колес. Угол поворота зубчатого колеса передачи от положения входа зуба в зацепление (точка a) до выхода его из зацепления (точка b) называется углом перекрытия. Отношение угла перекрытия к угловому шагу называется коэффициентом перекрытия (ε_γ). Расстояние p_α между одноименными боковыми поверхностями соседних зубьев, измеренное по линии зацепления, называется шагом эвольвентного зацепления. Отношение .

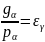2.2. Подбор чисел зубьев

1) Общее передаточное отношение редуктора определим по заданной частоте вращения электродвигателя и кривошипа:

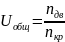, где

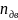- частота вращения электродвигателя,

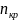- частота вращения кривошипа.

;

.

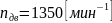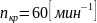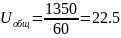
2) Передаточное отношение простой ступени с неподвижными осями колес:

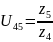, где

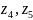- число зубьев колес.

;

.

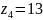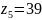3) Тогда передаточное отношение планетарной части редуктора будет равно:

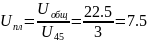
4) Передаточное отношение планетарного механизма заданной схемы определяется по формуле:

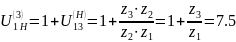
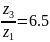
Если принять

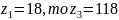
По условию соосности 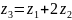определим число зубьев на сателлите:

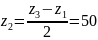
5) Максимально возможное число сателлитов находят по условию соседства:

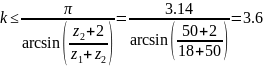
Из условия сборки:

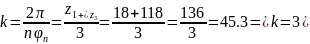
6) Подобрав числа зубьев колес планетарного механизма, определяем диаметры колес, предположив, что все колеса нулевые.

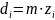
m – модуль зубчатых колес;

m = 10

;

;

;

;

.

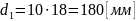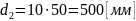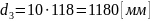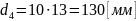Рассчитаем масштабные коэффициенты:

;

;

.
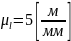
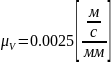
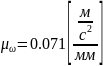