I.3. Собственные колебания упругой системы в горизонтальной плоскости.

I.3.1. Краткие теоретические предпосылки

Рис. 5. Расчетная схема

а – общий вид

б – траектория движения

в – схема действующих сил

0-0 – ось устойчивого равновесия

Груз массой m расположен на гладкой горизонтальной поверхности А-А между пружинами с жесткостью К₁ и К₂. Груз смещается вправо на расстояние Z и отпускается (Рис. 5). Система приходит в колебательное движение.

По второму закону Ньютона F-(F+KZ) = m·a, Н. (14)

Принимая во внимание, что получим дифференциальное уравнение движения , начальные условия при t = 0, Z = Z_0.

Решение уравнения имеет вид:

; (15)

Скорость движения: , м/с. (16)

Ускорение движения: , м/с². (17)

Заменяя колебательное движение равномерным вращательным с радиусом Z₀ и угловой скоростью , получаем:

, (18)

откуда , , .

I.3.2. Пример

Задача 1. Груз массой 0,5кг расположен на гладкой горизонтальной поверхности между пружинами с жесткостью 300 и 200 Н/м. Груз смещается на 0,15м от положения устойчивого равновесия и отпускается.

Определить:

а) период колебания системы;

б) частоту колебания системы;

в) наибольшую скорость и ускорение груза;

г) скорость и ускорение груза в момент его нахождения на расстоянии 0,1 м от положения устойчивого равновесия.

Решение: 1. Расчетная схема представлена на рис. 5.

2. Из уравнения движения:

,

,1/с,

,с,

.

3. Период колебания системы:

Т = 2·3,14· .

4. Частота колебания системы: 1/с.

5. Скорость движения груза:

м/с.

Наибольшая скорость движения груза:

.

6. Ускорение движения груза:

, м/с².

Наибольшее ускорение груза:

.

7. Скорость движения груза в момент его нахождения на расстоянии Z = 0,1м от положения устойчивого равновесия:

0,1 = 0,15 ; ;

,

следовательно .

8. Ускорение движения груза в момент его нахождения на расстоянии Z = 0,1м от положения устойчивого равновесия:

.

I.4 Свободные колебания упруго – вязкой системы

I.4.1. Краткие теоретические предпосылки

Приведенная на рис. 6. упруго – вязкая система состоит из массы на пружине и демпфера.

Демпфирующая сила принимается пропорциональной скорости движения. Демпфер представлен в виде поршня с отверстием в цилиндре с жидкостью.

Уравнение движения:

F – (F+KZ+C ) = ma = , (19)

или , (20)

где

С – постоянная демпфирования;

K – жесткость пружины.

Рис. 6. Расчетная схема

а – траектория движения

б – схема действующих сил

0-0 – положение устойчивого равновесия

Как показывает решение этого дифференциального уравнения, характер движения системы определяется значением постоянной демпфирования С (Рис. 7).

Критическим значением постоянной демпфирования является

, (21)

при имеют место затухающие колебания (Рис. 7а)

при колебательных движений в системе не будет.

Система без колебаний возвращается в исходное положение

(Рис. 7б).

I.4.2. Пример

Задача 1. Масса автомашины с пассажирами m = 1200кг. Осадка рессор h = 0,1м.

Определить значение постоянной демпфирования, при котором полностью исключается свободные колебания автомашины из–за неровностей дороги. Нагрузку на колеса автомашины принять одинаковой.

Решение 1.Нагрузка на колеса автомашины

,

где

m – масса автомашины с пассажирами, кг;

g – ускорение силы тяжести, м/с²;

4 – число колес автомашины.

2. Жесткость рессоры колеса

;

3. Полное гашение свободных колебаний автомашины имеет место при значении постоянной демпфирования амортизатора

.

I.5 Вынужденные колебания упругой системы

I.5.1. Краткие теоретические предпосылки

Рис. 8. Расчетная схема

Вынужденные колебания системы вызываются внешней силой Р, действующей на массу m, поддерживаемую пружиной с жесткостью К (Рис. 8). Действие силы Р изменяется по гармоническому закону:

Р = Р , Н (22)

где Р_о – амплитуда силы, Н;

- угловая скорость, 1/с;

t – время, с

Период вынужденных колебаний , с (23)

Частота колебаний , 1/с (24)

Уравнение движения имеет вид

, Н (25)

или , Н (26)

где

,

начальные условия: при t = 0,Z = Z₀,

где

Z₀ - амплитуда колебания массы.

Полное решение уравнения движения

,

; (27)

Разделив во втором слагаемом числитель и знаменатель на Kg получим:

.

Приведенное решение состоит из двух частей:

первая часть такая же, как при собственном колебании упругой системы с частотой .

вторая часть представляет непрерывное колебание под действием приложенной внешней силы Р с частотой колебаний .

График зависимости полного смещения Z массы m от времени t приведен на рис. 9.

Рис. 9. Развернутая диаграмма смещения Z

Выражение называется коэффициентом усиления колебаний.

Его можно представить в виде , (28)

где

- частота колебаний приложенной внешней силы;

- частота собственных колебаний системы;

Зависимость коэффициента усиления колебаний М от отклонения приведены на рис. 10.

Рис. 10. Зависимость коэффициента давления колебаний М от f/f_n

Критическое значение постоянной демпфирования:

, (29)

По мере того как , при отсутствии демпфирования.

Это называется явлением резонанса.

При коэффициент усиления колебаний М становится отрицательным, что соответствует движению массы m в противоположном направлении действия силы Р.

При приближении , когда чистота приложенной внешней силы становится очень большой относительно частоты собственных колебаний системы величин смещения .

Другими словами, тело массой m не успевает сместиться, как изменится направление действия силы. На рис. 10 показано семейство значений М для различных отношений значений постоянной демпфирования С к её критическому значению С_с.

С увеличением коэффициент усиления колебаний М снижается при его значение .

Закономерности вынужденных колебаний системы используются при устройстве сейсмографа (Рис. 11).

Рис. 11. Схема сейсмографа

Амплитуда смещения массы прибора относительно базы (почвы)

, (30)

где

- частота собственных колебаний прибора;

- частота колебаний почвы;

- смещение почвы.

В зависимости от жесткости пружин сейсмограф показывает смещение почвы (мягкая пружина) или ускорение смещения почвы (жесткие пружины).

I.5.2. Примеры

Задача 1. Масса загруженного товарного вагона (без ходовой части) кг, осадка рессор h = 0,1м, длинна рельса между стыками l = 18м.

Определить:

При какой скорости движения поезда возникает резонанс колебаний подвижного состава на стыках рельсов?

Решение: 1. Расчетная схема приведена на рис. 12.

2. условие резонанса колебаний ,

где

- период собственных колебаний системы, с;

период вынужденных колебаний системы, с;

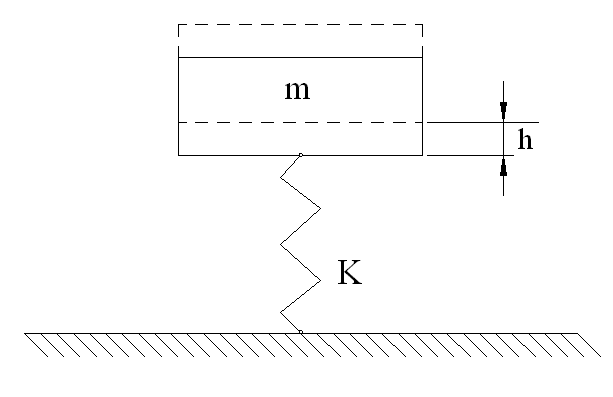
Рис. 12. Расчетная схема

3. Период собственных колебаний системы

, с

, Н/м

, с

где

m – масса вагона, кг;

К – жесткость рессор, Н/м;

g – ускорение силы тяжести, ;

h – осадка рессор, м.

4. Период вынужденных колебаний системы

,с

где

l - длина рельса между стыками, м;

V- скорость движения поезда, м/с.

5. Условие возникновение резонанса

,

откуда .

Задача 2. Частота колебаний сейсмографа , частота колебаний почвы ,1/с.

Определить:

Что показывает сейсмограф?

Решение: 1. Расчетная схема приведена на рис. 11.

2. Амплитуда смещения массы прибора относительно базы, закрепленной в почве ,

где

- частота собственных колебаний прибора, 1/с;

частота колебаний почвы, 1/с;

- амплитуда смещения почвы.

В нашем случае , следовательно, прибор замеряет амплитуду смещения почвы.

I.6. Задания для самостоятельной работы

Задание 1. Груз массой m кладется на пружину с жесткостью К. Значения m и К приведены в табл. 1.

Таблица 1

Показатель	Варианты
	1	2	3
m, кг	7	4	6
К, Н/м	5000	2500	4000

Определить: 1. Частоту и период собственных колебаний системы.

2. Скорости и ускорение груза для времени , , , ,

где

Т – период собственных колебаний системы, с.

Задание 2. Груз массой m расположен на гладкой горизонтальной поверхности между пружинами с жесткостью К₁ и К_2. Груз смещается вправо на расстояние Z₀ и отпускается. Система приходит в колебательное движение.

Определить: 1. Приод колебаний системы;

2. Частоту колебания системы;

3. Наибольшую скорость и ускорение груза;

4. Скорость и ускорение груза в момент его нахождения на расстоянии Z, от положения устойчивого равновесия. Значение m, K₁, K₂, Z₀ и Z, приведены в табл. 2.

Таблица 2

Показатель	Варианты
	1	2	3
m, кг	0,75	1,0	1,25
К1, Н/м	450	500	700
К2, Н/м	300	300	500
Z0, м	0,2	0,25	0,2
Z1, м	0,15	0,15	0,15

Задание 3. Масса загруженного товарного вагона m кг, осадка рессор h м, длина рельса между стыками l м. При какой скорости движения поезда возникает резонанс колебаний подвижного состава на стыках рельсов, если амортизаторы отсутствуют? Значения m и h приведены в табл. 3.

Таблица 3

Показатель	Варианты
	1	2	3
m, кг	9,2·105	8,8·105	8,5·105
Осадка рессор h,м	0,12	0,1	0,1
Длина рельсов l,м	18	18	35