32. Абсолютно і умовно збіжні ряди. Властивості

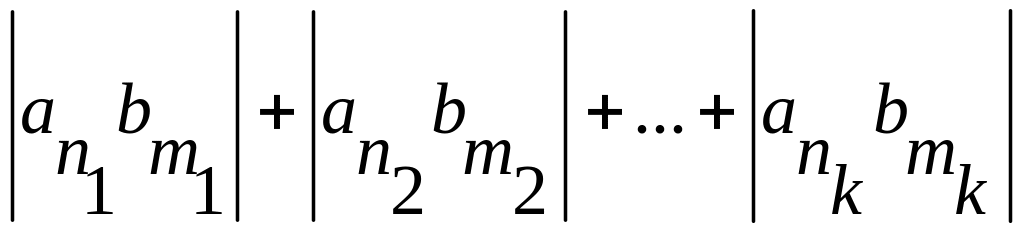
(*). = Оскільки обмежені в сукупності, то даний ряд збігається абсолютно. Покажемо, що . Складемо таблицю:

Запишемо ряд по таблиці наступним чином і отримаємо: . , , . , , .Звідки отримаємо потрібну рівність.

5. для абсолютно збіжних рядів має місце переставний, груповий і розподільний закони.

Для умовно збіжних рядів переставний закон не має місця.

Нехай - додатні члени ряду (1), а - від’ємні члени ряду (1).

Лема: Якщо ряд (1) збігається умовно , то ряди (3) , (4) розбіжні.

Доведення: Нехай ряд (1) збігається, тобто , і збігається один з рядів (3) або (4), наприклад ряд (3). Тоді , .

Якщо (4) збігається, то ; , ; , ; , Нехай - частинна сума ряду (2). , тобто частинна сума ряду (2) обмежена, що означає, що ряд (2) збігається. Отже, ряд (1) збігається абсолютно. Отримали суперечність.

Якщо (4) не збігається, тобто . Тоді (4) не перетворюється в скінчену суму , причому при , . При розгляді рівності отримаємо протиріччя.

Отже, ні один з рядів (3), (4) не збігаються, а отже дані два ряди є розбіжні. Лема доведена.

Для умовно збіжних рядів справедлива теорема Рімана.

Теорема(ознака Рімана): Якщо ряд (1) збігається умовно, то яке б не була число , члени даного ряду можна переставити так, що сума отриманого ряду буде рівна .

Для дослідження умовно збіжних рядів на збіжність використовують ознаку Абеля і Діріхле.

Нерівність Абеля: Якщо , , і , , то .

Ознака Діріхле: Якщо ряд такий, що послідовність монотонно спадна і збігається до нуля, а послідовність частинних сум ряду обмежена, тоді ряд збігається.

33. Функціональні ряди і послідовності. Рівномірна збіжність. Критерій рівномірної збіжності. Ознака Вейєрштрасса, Абеля, Діріхле.

Розглянемо послідовність функцій , –фіксуємо. При фіксованому ми маємо числову послідовність. . Нехай . Беремо інше фіксуємо, , і знов маємо числову послідовність . Нехай . Якщо для –фіксоване, , , то ми бачимо, що на визначена функція і цю функцію називають граничною функцією послідовності .

Озн.функціонального ряду і його суми. Нехай ми маємо (1), . (2), . (3). Нехай ряд (3) збіжний, і суму цього ряду позначимо , . Для фіксованих точок, де ряд (3) збіжний визначимо суму в кожній точці. Сукупність утворює область збіжності і є областю визначення його суми . Позначимо , , ..., – це -ні частинні суми функціонального ряду. Очевидно, що якщо –загальний член ряду (1). Необхідна умова збіжності (1): при кожному фіксованому з області збіжності. –залишок. Необхідна і достатня умова збіжності в кожній точці: .

Озн. рівномірної збіжності функціонального ряду. , якщо його залишок після -го члена рівномірно прямує до 0, тобто , .

Якщо область складається з скінченної кількості точок, то для кожної точки і серед них виберемо максимальне, і це максимальне буде обслуговувати всі . Якщо область має нескінченну кількість точок, то щоб вибрати максимальне повинні бути критерії рівномірної збіжності.

Озн. рівномірної збіжності. Для , що для .

Критерій Больцано-Коші. Щоб необхідно і досить, щоб для , і виконувалася нерівність , (*) .

Доведення. А) Необхідність. Нехай . Покажемо, що виконується (*). Сформулюємо озн. рівномірної збіжності: .

. . , коли .Б) Достатність. .Треба показати, що: 1) ;2) збіжність рівномірна. –фіксоване, тоді (*) має вигляд (**) , . (**)–це критерій Б-К. Існує скінченна границя для числової послідовності, тому в кожній фіксованій точці також існує границя. , . Гранична функція існує в кожній точці. В (**) перейдемо до границі, коли при кожному фіксованому . Отримаємо, що . Це і означає рівномірну збіжність. На практиці використовують (***)–необхідна і достатня умова, щоб була рівномірна збіжність.