30 Числові ряди. Збіжність. Необхідна умова збіжності. Необхідна і достатня умова збіжності.

Розглянемо числову послідовність загальний член послідовності. Утворимо такий символ (1), такий символ називається числовим рядом.

Позначимо через

, , ……. , ,… , - на частинна сума ряду (1). Знайдемо , якщо така границя існує і є скінченим числом, то кажуть, що ряд (1) є збіжним. Якщо або не існує взагалі, то (1) розбіжний. Якщо в ряді(1) відкинути перші членів, то отримаємо ряд 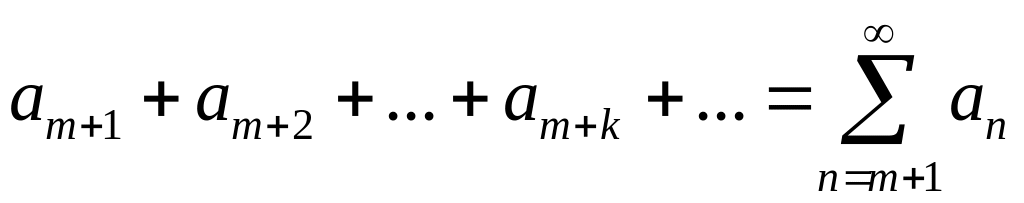, (2) . Такий ряд називається залишком ряду (1) після го члена.

Теорема

Якщо, збігається ряд (1), то збігається і будь – який його залишок. Навпаки, із збіжності залишку (2) випливає збіжність ряду (1).

Доведення. Зафіксуємо і позначимо - ту частинну суму ряду (2) через :

Тоді , . Якщо ряд (1) збігається, так, що , то при необмеженому зростанні існує скінчена границя і для суми , а це означає збіжність ряду (2). Навпаки, нехай збігається ряд (2), , тоді , звідси при необмеженому зростанні частинна сума має границю тобто збігається ряд (1). Теорему доведено.

Необхідною і достатньою умовою збіжності будь – якого числового ряду є збіжність до нуля його залишку .

Якщо ряд збіжний, то , 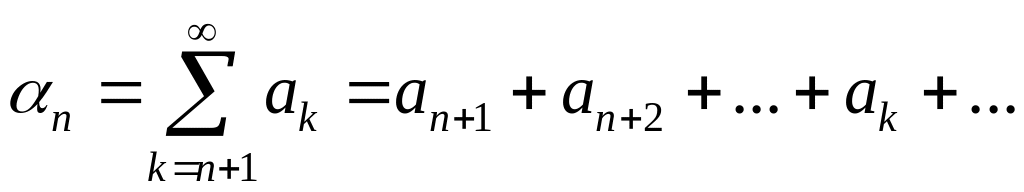.Звідси видно, що повинно прямувати до нуля. Якщо залишок , то ряд збіжний.

Необхідна умова збіжності.

Загальний член збіжного ряду прямує до нуля.

Це видно з того, що раз (а з ним і ) мають скінчену границю , то . Зауважимо, що з того що загальний член прямує до нуля не слідує, що ряд збіжний.

Критерій Больцано - Коші збіжності числового ряду.

необхідно і досить, щоб

31 Ознаки збіжності додатніх рядів

Нехай дано два ряди з додатніми членами

(1), (2)

Теор.1. Коли кожен член ряду (1) не більший від відповідного члена ряду (2), тобто , і коли ряд (2) збігаєт., то ряд (1) також збігаєт.

Довед. Припустимо, що

і при зростанні індекса не спадають: і дістаємо з і додаванням до них невід’ємних доданків і . Оск. , за умовою, прямує до – познач. її через , – то при всякому . Але з умовую теор. узгоджується також ; значить при всякому . Отже, при є неспадна і обмеж. ф–я; тому прямує до границі.

Теор. 2. Коли кожний член ряду (1) не менший від відповідного члена ряду (2), тобто , і ряд (2) розбіж., то ряд (1) також розбіжн.

Довед. Через те що 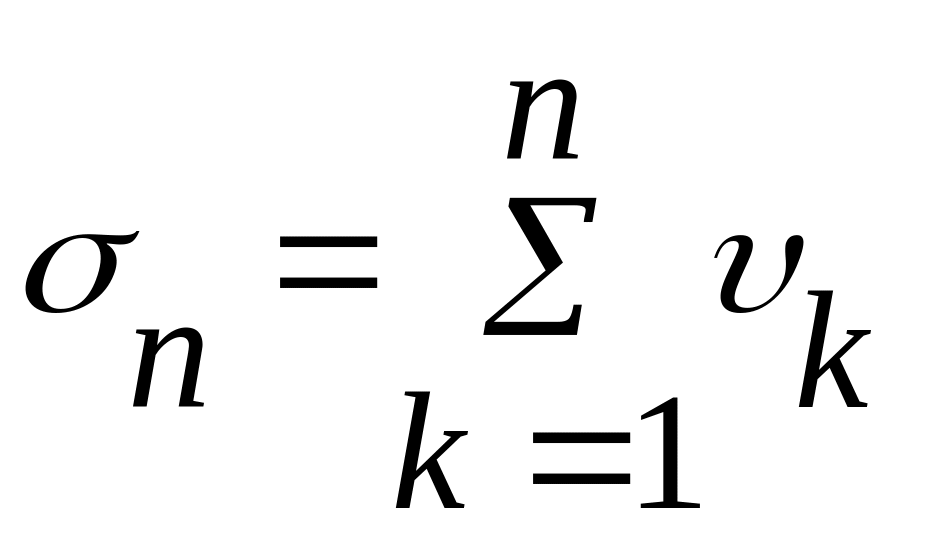не спадає, то розбіжн. ряду (2) може виникати тільки внаслідок того, що . Але, за умовою, що і, отже, також необмежено зростає прни , тобто ряд (1) розбіжн. Що й треба було довести.

Ознака Даламбера. Коли при існує границя відношення 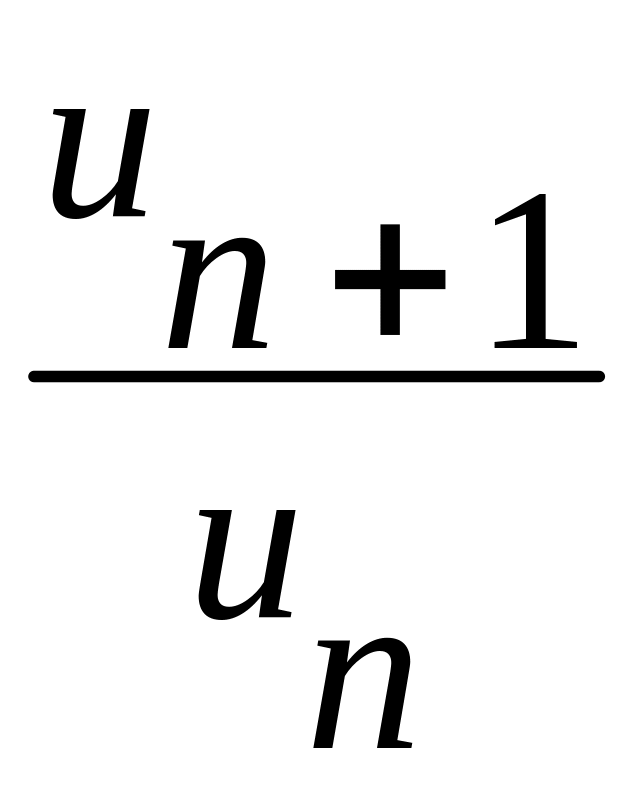, що дорівнює ,

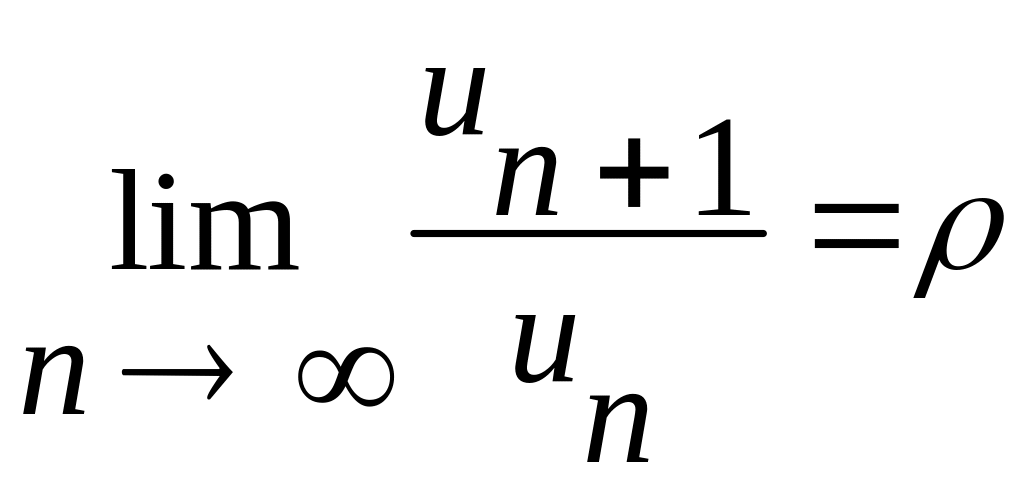,то при ряд збіг., при ряд розбіг. При ряд може бути як збіжн., так і розбіжн.

Довед. Нех. ; завжди можна вибрати таке , що при буде справедлива рівність

де берет. настільки мале, щоб ще залишалося меншим 1. Але тоді на підставі загальної ознаки Даламбера робимо висновок, що рядзбіг.

Нехай ; ми можемо вибрати таке , що при матиме місце нерівн.

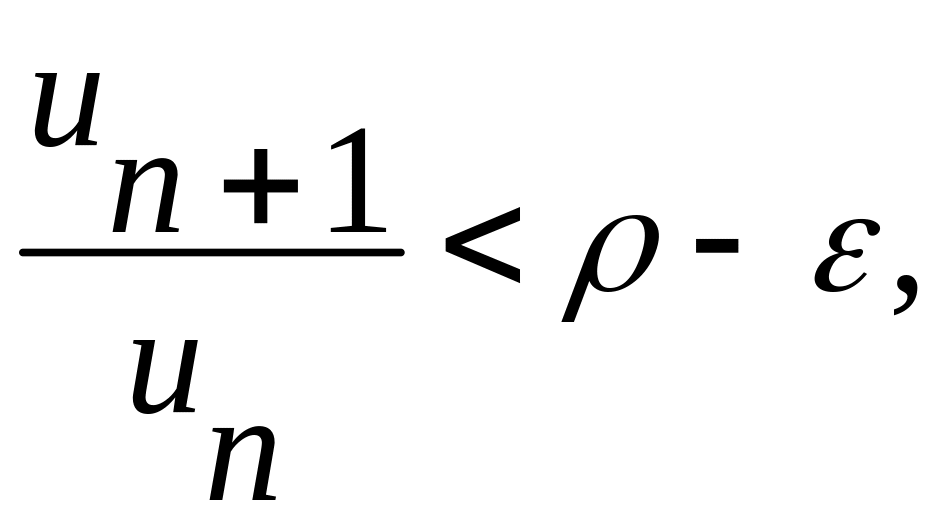де берет. настільки мале, щоб ще залиш. більшим від 1; на підставі загальної ознаки Даламбера робимо висновок, що ряд розбіг.

Нарешті, нех. . Як приклад візьмемо ряд , для якого

при незалежно від величини показника . Разом з тим нам відомо, що при цей ряд розбігається, а при – збігається. Так що при нічогог не можна сказати про збіжн. ряду.