- •30 Числові ряди. Збіжність. Необхідна умова збіжності. Необхідна і достатня умова збіжності.
- •31 Ознаки збіжності додатніх рядів
- •31 Ознаки збіжності додатніх рядів
- •32. Абсолютно і умовно збіжні ряди. Властивості.
- •32. Абсолютно і умовно збіжні ряди. Властивості
- •33. Функціональні ряди і послідовності. Рівномірна збіжність. Критерій рівномірної збіжності. Ознака Вейєрштрасса, Абеля, Діріхле.
- •33. Функціональні ряди і послідовності. Рівномірна збіжність. Критерій
- •34. Степеневі ряди.Інтервал і радіус збіжності.Абсолютна,умовна і рівномірна збіжність.
33. Функціональні ряди і послідовності. Рівномірна збіжність. Критерій
рівномірної збіжності. Ознака Вейєрштрасса, Абеля, Діріхле.
Ознака
Вейєрштрасса.
Нехай
![]() (2);
визначена для
і 1)
(2);
визначена для
і 1)![]() ;
2)
;
2)
![]() ;
тоді (2) збігається абсолютно і рівномірно
до своєї суми,
;
тоді (2) збігається абсолютно і рівномірно
до своєї суми,
![]() .
.
Доведення.
Перевіримо виконання критерію Б-К
рівномірної збіжності. Розглянемо
(![]() –мажоранти
для
).
Для цього ряду можна сформулювати
критерій Б-К збіжності числового ряду.
Для
–мажоранти
для
).
Для цього ряду можна сформулювати
критерій Б-К збіжності числового ряду.
Для
![]() ,
що для
і для
,
що для
і для
![]() .
Треба показати, що для
.
Треба показати, що для
![]() ;
;
![]() .Треба
знайти
.Треба
знайти
![]() ,
щоб
виконувалась
,
щоб
виконувалась
![]() .
.
![]() .
.
![]() .
Видно,
що є рівномірна збіжність і ряд крім
того, а також ряд з абсолютних величин
також рівномірно збігається. Цю ознаку
добре застосовувати для таких рядів:
.
Видно,
що є рівномірна збіжність і ряд крім
того, а також ряд з абсолютних величин
також рівномірно збігається. Цю ознаку
добре застосовувати для таких рядів:
![]() .
Якщо послідовність або ряд рівномірно
збігається, то яку б ми послідовність
чисел
.
Якщо послідовність або ряд рівномірно
збігається, то яку б ми послідовність
чисел
![]() не взяли, таку що
,
то завжди члени ряду можна взяти в дужки
так, щоб утворений ряд мав ряд
за мажорантом
не взяли, таку що
,
то завжди члени ряду можна взяти в дужки
так, щоб утворений ряд мав ряд
за мажорантом
![]() .
Ще є дві ознаки рівномірної збіжності.
Це ознак Абеля і Діріхле, але тут ряди
збігаються рівномірно, але не абсолютно.
.
Ще є дві ознаки рівномірної збіжності.
Це ознак Абеля і Діріхле, але тут ряди
збігаються рівномірно, але не абсолютно.
Ознака
Абеля і Діріхле.
![]() (1).
(1).![]() .
.
Ознака
Абеля.
Нехай:
1) ряд складений з
![]() збігається
рівномірно до своєї суми
збігається
рівномірно до своєї суми
![]() ,
,
![]() ;
2)
;
2)![]() ,
при кожному фіксованому
,
монотонна функція по
і обмежена для
,
при кожному фіксованому
,
монотонна функція по
і обмежена для
![]() .
Тоді
.
Тоді
![]()
Доведення.
Ознака Абеля для ряду (*) читається так:
Якщо 1)![]() ;
2)
;
2)
![]() –монотонна
послідовність по
і
–монотонна
послідовність по
і
![]() ,
то ряд (*) збігається умовно,
,
то ряд (*) збігається умовно,
![]() .
Доведення цієї ознаки ґрунтується на
перетвореннях Абеля. При кожному
фіксованому
ряд (1) є числовим рядом, до якого
застосована ознака Абеля (*), тому при
кожному фіксованому
.
Доведення цієї ознаки ґрунтується на
перетвореннях Абеля. При кожному
фіксованому
ряд (1) є числовим рядом, до якого
застосована ознака Абеля (*), тому при
кожному фіксованому
![]() .
При кожному фіксованому
справедлива теорема Абеля. Отже,
.
При кожному фіксованому
справедлива теорема Абеля. Отже,
![]() ,
де роль
,
де роль
![]() відіграє
відіграє
![]() ,
а всі
,
а всі
![]() обмежені. Аналогічно доводиться ознака
Діріхле як для числових рядів.
обмежені. Аналогічно доводиться ознака
Діріхле як для числових рядів.
Ознака
Діріхле.
Нехай: 1)![]() ;
2)
;
2)![]() і при кожному фіксованому
,
і при кожному фіксованому
,
![]() монотонна
функція по
,
тоді
монотонна
функція по
,
тоді
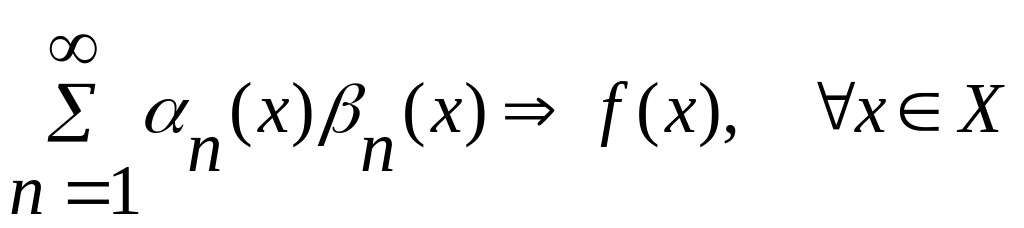 .
.
34. Степеневі ряди.Інтервал і радіус збіжності.Абсолютна,умовна і рівномірна збіжність.
![]()
![]() ;
;
![]() ,…,
,…,![]() ,…
,…![]() ;
;
![]() ;
;
![]() ;
-- коефіцієнти
;
-- коефіцієнти
![]() .
Щоб надати змісту цьому символу,розглянемо
дійсне x
і фіксуємо його. Якщо
при фіксов.
.
Щоб надати змісту цьому символу,розглянемо
дійсне x
і фіксуємо його. Якщо
при фіксов.
![]()
![]() -збігається,то
це є
-збігається,то
це є
![]() [
[![]() =
=![]() .
.
Знайдемо
![]() ,при
яких (1)-збіж. Ця множина іксів назив.областю
збіж. (1),тому сума (1) є функцією
,
яка визначена на тих х, де є збіж. цього
ряду.яка ж обл. збіж. Ряду (1)?
,при
яких (1)-збіж. Ця множина іксів назив.областю
збіж. (1),тому сума (1) є функцією
,
яка визначена на тих х, де є збіж. цього
ряду.яка ж обл. збіж. Ряду (1)?
(1)-степеневий. Для
зручності
![]() ,
тоді
,
тоді
 ;
;
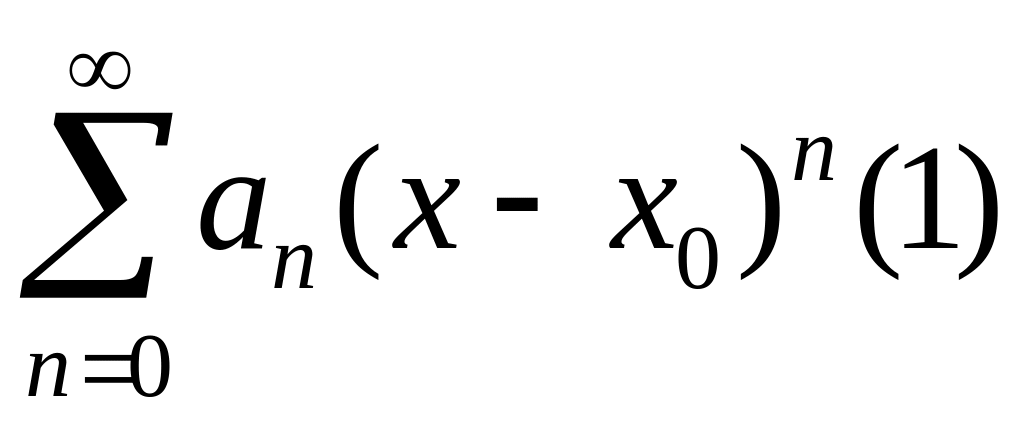
Теорема Абеля:Якщо
ряд
 збіг.
в точ.
збіг.
в точ.![]() ,то
ряд збіг. в
,які
,то
ряд збіг. в
,які
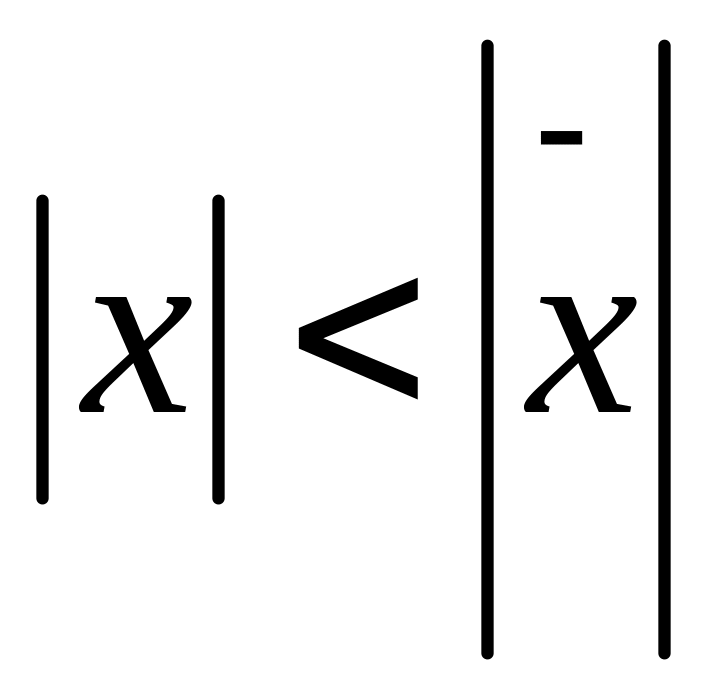 На цьому інтервалі для всіх точ.є збіж.
Областю збіж може бути інтервал,вся
вісь,або точ. 0.
На цьому інтервалі для всіх точ.є збіж.
Областю збіж може бути інтервал,вся
вісь,або точ. 0.
Доведення.
 ;
Викон.умова збіж. Загальний член
;
Викон.умова збіж. Загальний член
![]() ;
;
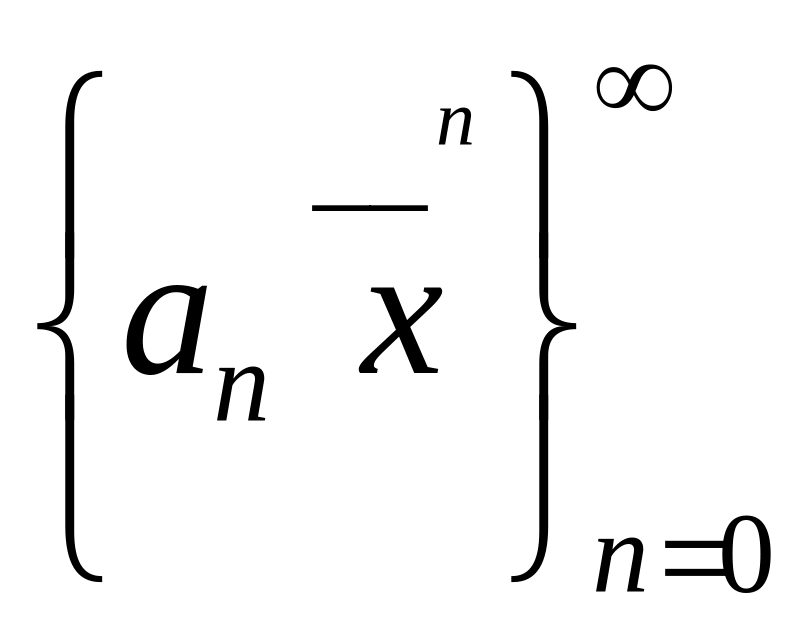 __має
границю,то вона обмежена. Тому для
__має
границю,то вона обмежена. Тому для
![]() ,
,
![]() ,що
,що
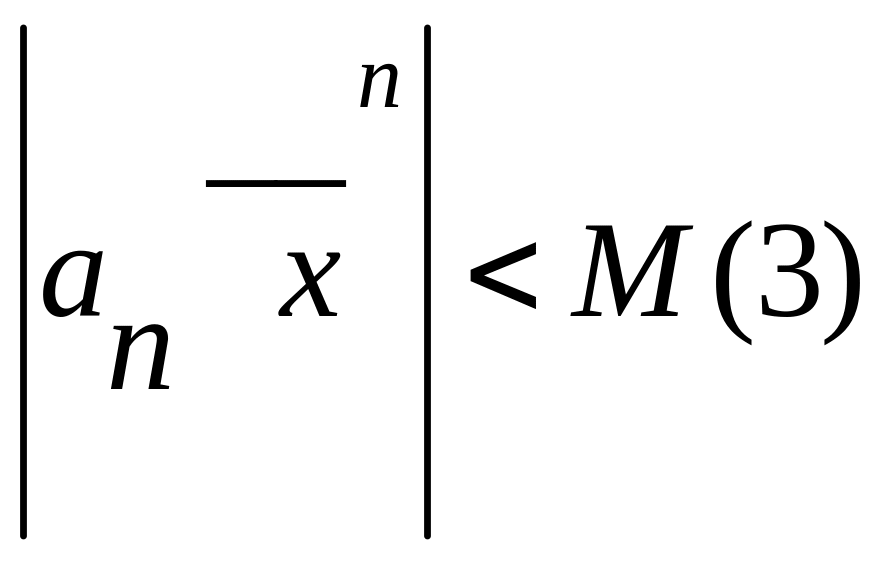 Запишемо
ряд для
,що
Запишемо
ряд для
,що![]() ,тоді
,тоді
![]()
![]()
 Доведено.
Доведено.
Областю збіж може
бути інтервал,вся вісь,або точ. 0.
R-половина
довжини інтервалу,то це радіус збіжності.
R=0;
R=+![]() ;
R-знаходимо
за ознакою Коші або Даламбера.
;
R-знаходимо
за ознакою Коші або Даламбера.
Знаходження
радіуса збіж.степ.ряду.Маємо
ряд
![]() ;
-загаль.член
ряду.
;
-загаль.член
ряду.
![]() ;
Необх.умова
;
Необх.умова
![]() ,
,![]() .
З теореми Абеля
.
З теореми Абеля
![]() ,то
.
,то
.
Розгляд.
![]() ,то
,то
![]() Застос.ознаку Даламбера
Застос.ознаку Даламбера
![]() ;
;
![]()
![]() ,тоді
(4) і (1) збіж.;
,тоді
(4) і (1) збіж.;
![]() =
= -достатня
умова збіж.за ознакою Даламбера.
-достатня
умова збіж.за ознакою Даламбера.
![]() ;
Проаналізуємо (6).
;
Проаналізуємо (6).
1)
 =0;
=0;
![]() =
.
Для
викон.(6).
=
.
Для
викон.(6).
2)
=+
.
Якщо
![]() ,
то (6 не викон. Степ.ряд розбіжний. Збіжний
тільки в одній точ.
і
радіус збіж. R=0.
(
)
,
то (6 не викон. Степ.ряд розбіжний. Збіжний
тільки в одній точ.
і
радіус збіж. R=0.
(
)![]() =
=0
=
=0
3)
![]() =А
=А![]() ;
;
![]() ;
;
![]() -радіус
збіжності.
-радіус
збіжності.
![]() -інтервал
збіжності. З аналізу 1),2),3) маємо
-інтервал
збіжності. З аналізу 1),2),3) маємо
 .
В кожній точ.інтервалу збіж.ряд (1)
збіг.абсолютно.Виникає питання,що
робиться на кінцях інтервалу.Накінцях
інтервалу можуть бути різні випадки
залежно від ряду,їх треба досліджувати
окремо.
.
В кожній точ.інтервалу збіж.ряд (1)
збіг.абсолютно.Виникає питання,що
робиться на кінцях інтервалу.Накінцях
інтервалу можуть бути різні випадки
залежно від ряду,їх треба досліджувати
окремо.
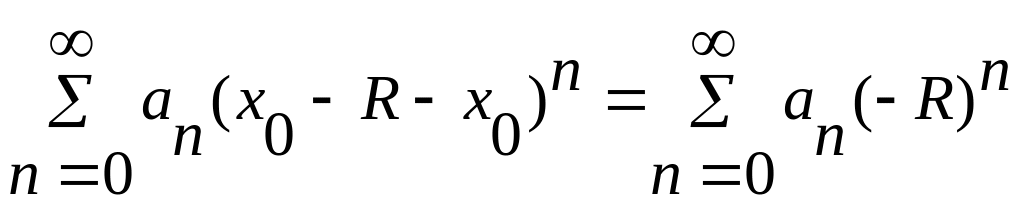 ;
;