31 Ознаки збіжності додатніх рядів

Ознака Коші. Коли при існує границя ,

то при ряд збігається, при ряд розбігається. При може бути як збіжним, так і розбіжним. Доведення цілком таке саме, як і в ознаці Даламбера.

Інтегральна ознака Коші. Коли члени ряду

можна розглядати як значення якоїсь додатної неперервної і спадної в інтервалі від до ф–ї при цілих значеннях аргументу :

то ряд збігається, коли невласний інтеграл

збігається, і розбігається, коли цей інтеграл розбігається.

Довед. Розгл.. криволінійну трапецію, обмежену лінією , з основою від до , – довільне ціле додатне число(мал. 1)

Площа її вимірюється інтегралом

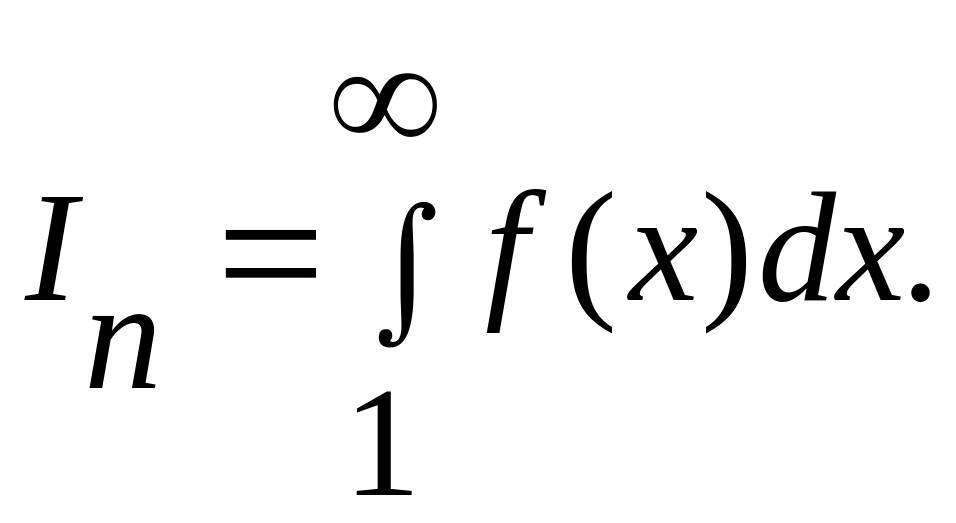
Позначимо цілі точки основи: . Цим точкам відповідають дві східчасті фігури (мал. 1):одна з них має площу, що дорівнює , а друга – площу, яка дорівнює . Площа першої фігури менша за площу даної криволінійної трапеції, площа другої – більша за неї, тобто маємо

Звідси дістаємо дві нерівності:

(*)

(**)

1) Нехай існує; тоді , і з нерівності (*) при всякому знаходимо:

Таким чином, як зростаюча і обмежена ф–я має границю і, отже, ряд збіг.

2) Нехай не існує; тоді при , і на основі нерівності (**) робимо висновок, що також необмежено зростає, тобто ряд розбігається.

32. Абсолютно і умовно збіжні ряди. Властивості.

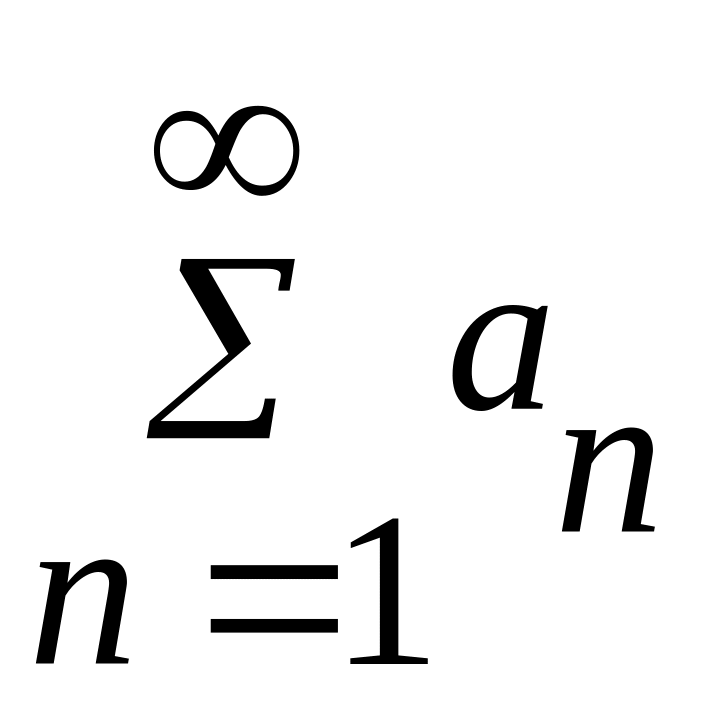
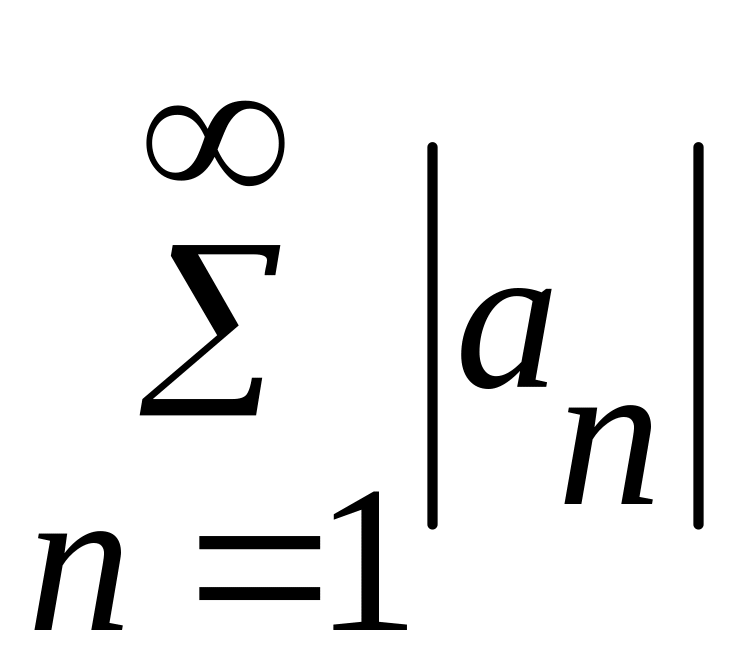Нехай дано ряд (1) (2)

Озн. Якщо разом з рядом (1) збігається ряд складений з абсолютних величин членів даного ряду, то ряд (1) наз. абсолютно збіжним; якщо ряд (1) збігається , а ряд складений з абсолютних величин розбігається, то ряд (1) наз. не абсолютно(умовно) збіжним.

Теорема Коші(про абсолютну збіжність): Якщо збігається ряд (2), то збігається (1).

Доведення: Перевіримо для ряду (1) виконання критерію збіжності Больцана-Коші, тобто: що виконується рівність .

Оскільки (2)- збіжний, то для нього виконується критерій Больцана-Коші, тобто : що виконується рівність .

,отже , . Теорема доведена.

На абсолютну збіжність ряди перевіряють так:

1.Якщо , при , то ряди (1) і (2) – розбіжні.

2. Якщо , при , то виконується тільки необхідна умова. Складаємо ряд (2)- це додатній ряд і до нього можна застосувати ознаки порівняння: - ознака Коші; - ознака Даламбера; - ознака Раабе;

Можна використовувати теорему Больцана-Коші. Але якщо ми показали, що ряд (2) розбіжний, то треба досліджувати за критерієм Больцана-Коші через залишок, або через означення збіжності ряду.Над збіжними рядами можна виконувати такі операції, як додавання, віднімання, множення на число, множення двох рядів:

1.якщо ряд збігається абсолютно, то ряд, який складений з тих самих елементів, але в іншому порядку, також збігається абсолютно до того самого числа.

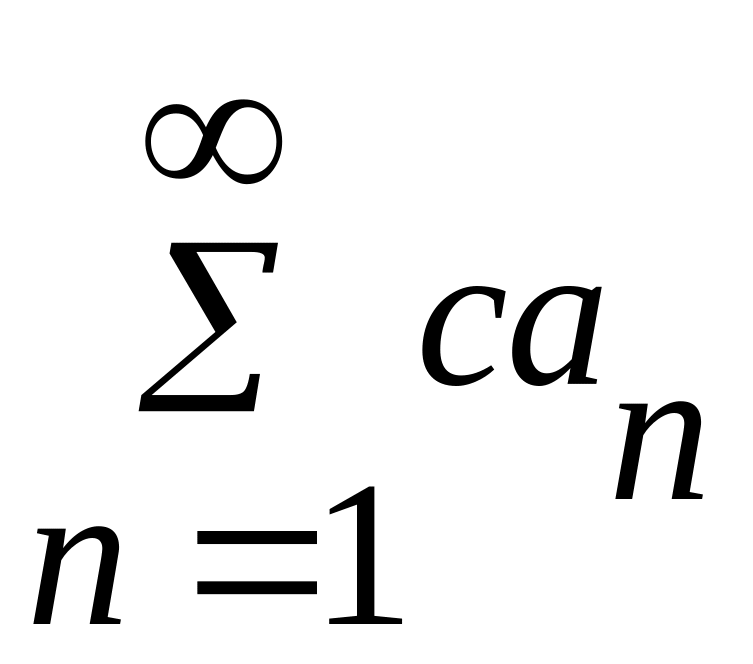2. якщо ряд (1) абсолютно збіжний і - деяке число, то ряд також збіжний.

3.якщо ряди (1) , 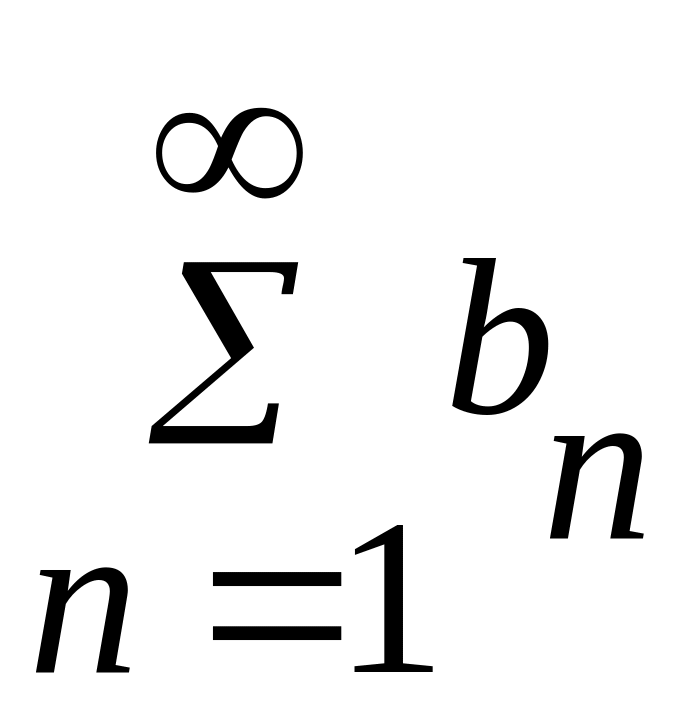(3) абсолютно збіжні, то ряд також абсолютно збіжний.

4.якщо (1) і (3) абсолютно збіжні, то ряд, отриманий з всеможливих добутків членів даних рядів також збігається абсолютно, причому якщо сума даного ряду рівна , а суми рядів (1) і (3) відповідно і , то .

Доведення: із всеможливих добутків складаємо суму (*) . Покажемо, що дана сума абсолютно збіжна. 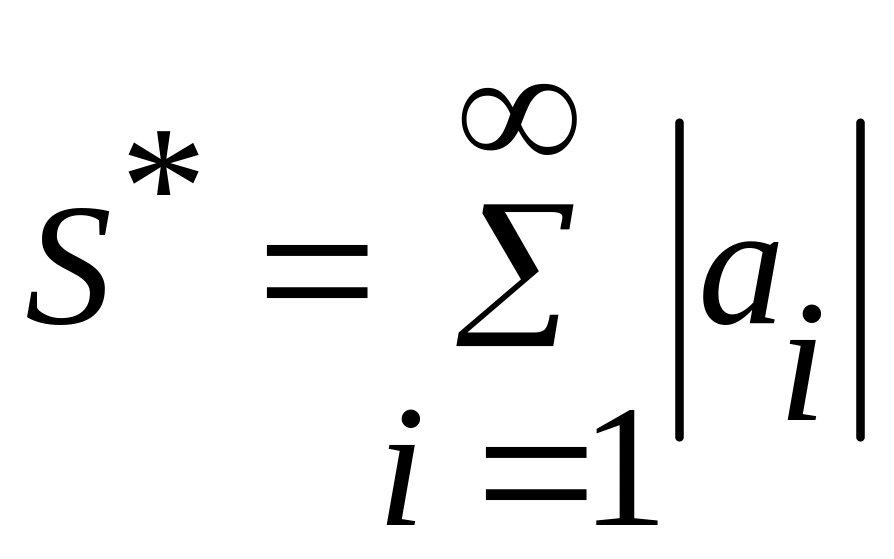, , 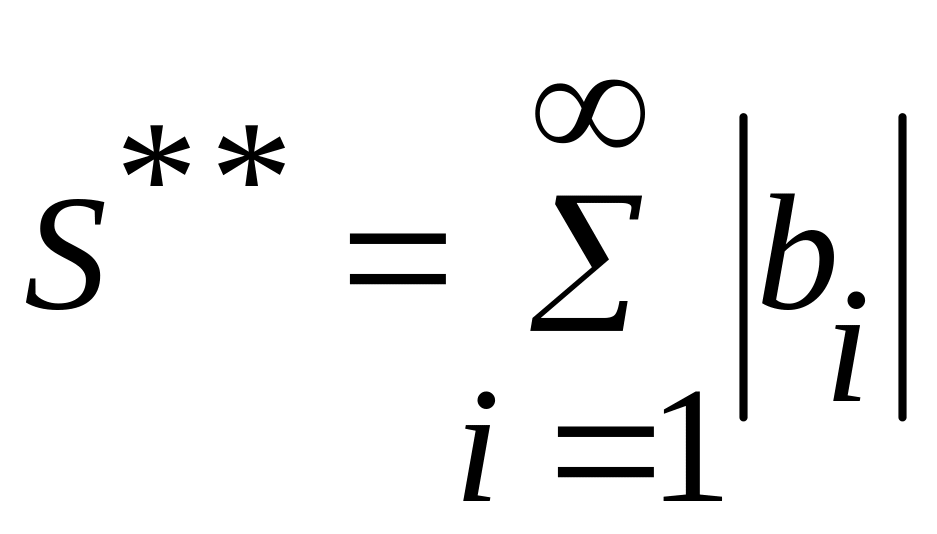скінченні величини. Розглянемо частинні суми ряду, складеного з абс. величин членів ряду.