Виды подграфов

Пусть дан граф G = (X, A), где X = {хi}, i = 1, 2, ..., n – множество вершин, A = { ai }, i = 1, 2, ..., m – множество дуг.

Подграфом G'= (X', A') исходного графа G называется такой граф G', для которого X' X и A' A. Примеры подграфов показаны на рис. 6.1,б), а исходный граф – на рис. 6.1,а.

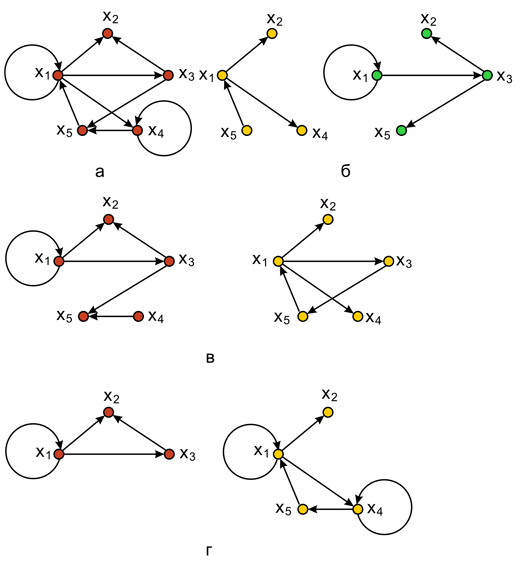
Рис. 6.1. Виды подграфов: а – исходный граф; б – подграфы; в – остовные подграфы; г – порожденные подграфы

Остовным подграфом Gp = (X, Ap ) графа G называется граф, для которого Ap A. Таким образом, остовный подграф имеет то же самое множество вершин, что и исходный граф G, но множество дуг подграфа Gp является подмножеством множества дуг исходного графа. Примеры остовных подграфов приведены на рис. 6.1,в. Для графа, имеющего m дуг, можно построить k остовных подграфов

Порожденным подграфом Gs =(Xs , Гs ) называется граф, для которого Xs X и для каждой вершины хi Xs прямое отображение Гs (хi) = Г(хi) Xs . Таким образом, порожденный подграф состоит из подмножества вершин Xs множества вершин исходного графа и всех таких дуг графа G, у которого конечные и начальные вершины принадлежат подмножеству Xs . Примеры порожденных подграфов приведены на рис. 6.1,г.

В качестве иллюстративного примера рассмотрим граф, вершины которого представляют сотрудников некоторого учреждения, а дуги – линии связи между сотрудниками. Тогда граф, представляющий только наиболее важные связи или каналы связи данного учреждения, является остовным подграфом; граф, который подробно описывает линии связи только какой-то части учреждения (например, отдела), является порожденным подграфом, а граф, который представляет только важные линии связи в пределах отдела, является просто подграфом.

Маршруты, пути

Маршрут в графе - это последовательность вершин Х1,Х2..,Хn такая, что для каждого і=1,2..n-1 вершиныXi Xi+1 и соединены ребром. Эти n-1 ребер называются ребрами маршрута. Говорят, что маршрут проходит через них, а число n-1 называют длиной маршрута. Говорят, что маршрут соединяет вершины X1 и Xn, они называются соответственно началом и концом маршрута, вершины X2..Xn-1называются промежуточными. Маршрут называется замкнутым, если X1=Xn.

Путь - это маршрут, в котором все ребра различны. Путь называется простым, если и все вершины в нем различны.

.

Алгоритм Мальгранжа — разбиение графов на сильно связные под-графы.

Алгоритм

Пусть дан граф G=(X, A), где X={ хi }, i =1, 2, … , n — множество вершин, а A={ ai }, i =1, 2, …, m — где множество дуг, описанных матрицей смежности. Алгоритм разбиения заключается в следующем.

1)Для произвольной вершины хi ∈ X находим прямое T+(хi) и обратное T-(хi) транзитивные замыкания.

2)Находим T+(хi) ∩ T-(хi). Множество вершин этого пересечения составляют вершины максимального сильно связного подграфа G1 = (Х1, A1).

3)Из исходного графа вычитаем подграф G1:G '=G\G1, Х=X\Х1 .

4)Граф G 'принимаем за исходный граф и пока X ' ≠ Ø пункты 1, 2, 3 алгоритма повторяются.