Списком называется линейно – упорядоченная последовательность элементов данных Е.(1), Е(2), ..., Е(п), n > О, причем каждый элемент характеризуется одним и тем же набором полей. С другой стороны, упорядоченность элементов может задаваться с помощью специальных указателей или связок, располагаемых в элементах и дающих возможность для каждого элемента определить его предшественника или последователя или того и другого, Такие списки называются связными. При постоянном значении и соответствующем выборе элемента данных последовательный список сводится к вектору, массиву, записи или таблице. Стек – линейный список, в котором все включения и исключения (и обычно всякий доступ) делаются в одном конце списка. Очередь – линейный список, в котором все включения производятся на одном конце списка, а все исключения (и обычно всякий доступ) делаются на другом его конце. 􀂃 Дек (очередь с двумя концами) – линейный список, в котором все включения и исключения (и обычно всякий доступ) делаются на обоих концах списка. Следовательно, дек обладает большей мощностью, чем стек или очередь; он имеет некоторые общие свойства с колодой карт (в английском языке эти слова созвучны). Механизм стека часто помогает понять аналогия с переключением железнодорожных путей. Стек - это линейный список, в котором все включения и исключения (и обычно всякий доступ) делаются в одном конце списка. Это последовательный список с переменной длиной. Его еще называют «магазин», «очередь» по принципу "LIFO" (последним пришел, первым исключился). Примерами стека являются винтовочный магазин и железнодорожный разъезд для сортировки вагонов. Важнейшие операции доступа к стеку - включение и исключение элементов. Они осуществляются с вершины стека, причем в каждый момент времени для исключения доступен элемент Е, находящийся на вершине стека. Вершина стека адресуется с помощью специального указателя. При исключении элемента из стека сначала прочитывается информация об исключаемом элементе по значению указателя, а затем указатель смещается «вниз» на один слот. Стек считается пустым, если

указатель смещен «вниз» на длину одной ячейки относительно низа стека адресует первую свободную ячейку стека. Для хранения стека отводится сплошная область памяти. Размер ее достаточен для хранения максимального числа элементов. Граничные адреса этой области являются параметрами физической структуры стека. Если в процессе заполнения стека указатель, перемещаясь «вверх», выходит за границу первоначально отведенной области памяти, то происходит переполнение стека. В результате этого становится невозможным включение в стек нового элемента. Таким образом, хотя длина стека может измениться в процессе его

использования, эти изменения не должны выходить за пределы фиксированного участка памяти. Поэтому стек - полустатическая структура данных.

Дек

Особым типом списка является дек. Его название произошло от английского слова deque - double-ended queue - очередь с двумя концами. Дек представляет собой последовательный список, в котором как включение, так и исключение элементов, то есть всякий доступ, могут осуществляться с любого из двух копир» описка. Логическая и физическая структуры дека соответствуют логической и физической структурам очереди, но вместо терминов «хвост» и «голова» применяются термины «левый» и «правый» конец. Важнейшими операциями над деком, как и над простой очередью, являются операции включения и исключения элементов. Они представляют собой развитие и обобщение соответствующих операций с очередью. Дек обладает большей общностью, чем стек или очередь; он имеет некоторые общие свойства с колодой карт (в английском языке эти слова созвучны). Мы будем различать деки с ограниченным выходом или ограниченным входом: в таких деках соответственно исключение или включение допускается только на одном конце. Многие люди независимо поняли важность стеков и очередей и дали другие названия этим структурам; стек называли пуш-даун (push-down) списком, реверсивной памятью, гнездовой памятью, магазином, списком типа LIFO ("last-in-first-out" — "последним включается — первым исключается") и даже употребляется такой термин, как список йо-йо! Очередь иногда называют — циклической памятью или списком типа FIFO ("first-in-first-out" — "первым включается — первым исключается"). В течение многих лет бухгалтеры использовали термины LIFO и FIFO как названия методов при составлении прейскурантов. Еще один термин "архив"

применялся к декам с ограниченным выходом, а деки с ограниченным входом называли "перечнями" или "реестрами". Такое разнообразие названий интересно само по себе, поскольку оно свидетельствует о важности этих понятий. Слова "стек" и "очередь" постепенно становятся стандартными терминами; из всех других словосочетаний, перечисленных выше, лишь

"пуш-даун список" остается еще довольно распространенным, особенно в теории автоматов. Стеки очень часто встречаются в практике. Простым примером может служить ситуация, когда мы просматриваем множество данных и составляем список особых состояний или объектов, которые должны обрабатываться позднее; когда первоначальное множество обработано, мы возвращаемся к этому списку и выполняем последующую обработку, удаляя элементы из списка, пока список не станет пустым. Для этой цели пригодны как стек, так и очередь, но стек, как правило, удобнее. При решении задач наш мозг ведет себя, как "стек": одна проблема приводит к другой, а та в свою очередь к следующей; мы накапливаем в стеке эти задачи и подзадачи. При описании алгоритмов, использующих такие структуры, принята специальная терминология; так, мы помещаем элемент наверх стека или снимаем верхний элемент. Внизу стека находится наименее доступный элемент, и он не удаляется до тех пор, пока не будут исключены все другие элементы. Часто говорят, что элемент опускается (push down) в стек или что стек поднимается (pop up), если исключается верхний элемент. Эта терминология берет свое начало от "стеков" закусок, которые можно встретить в кафетериях, или по аналогии с колодами карт в некоторых перфораторных устройствах. Краткость слов "опустить" и "поднять" имеет свое преимущество, но эти термины ошибочно предполагают движение всего списка в памяти машины. Физически, однако, ничего не опускается;

элементы просто добавляются сверху, как при стоговании сена или при укладке кипы коробок. Таким образом, мы находим, что в наших алгоритмах применимо богатое разнообразие описательных слов: "сверху — вниз" — для стеков, "слева — направо" — для деков и "ожидание в очереди" — для очередей.

Дерево-одна из самых распространенных структур., используемых для представления данных в ЭВМ. А вообще, дерево-конечное множество, состоящее из одного или более элементов, называемых узлами. Между узлами существует отношение типа "исходный- порождённый". Корень - узел, не имеющий исходного (отца). Все узлы, кроме корня, имеют только один исходный (исх.отца). Есть деревья, состоящие из одного корня. Каждый узел может иметь несколько порождённых (сыновей). Отношение "исходный-порождённый" действует только так: не бывает отношения "порождённый-исходный", т.к потомок узла никогда не станет его предком. Определим формально дерево как конечное множество Т, состоящее из одного или более узлов, таких, что

а) имеется один специально обозначенный узел, называемый корнем данного дерева.

б) остальные узлы (исключая корень) содержатся в m≥0 попарно непересекающихся множествах Т1, …, Тm, каждое из которых в свою очередь является деревом. Деревья Т1, …, Тm называются поддеревьями данного корня. Из определения следует, что каждый узел дерева является корнем

некоторого поддерева, которое содержится в этом дереве. Число поддеревьев данного узла называется степенью этого узла. Узел с нулевой степенью называется концевым узлом; иногда его называют листом. Неконцевые узлы часто называют узлами разветвления. Уровень узла по отношению к дереву Т определяется следующим образом: говорят, что корень имеет уровень 1, а

другие узлы имеют уровень на 1 выше их уровня относительно содержащего их поддерева Тj этого корня. Определим бинарное дерево как конечное множество узлов, которое или пусто, или состоит

из корня и из двух непересекающихся бинарных деревьев, называемых левым и правым поддеревьями данного корня.

Помимо таких структур, как деревья, леса и бинарные деревья, имеется тип, тесно связанный с первыми двумя. Эти структуры называют обычно списочными структурами. Такой список определяется как конечная последовательность списков, число которых, может быть, и равно нулю. Представление бинарного дерева в компьютере вытекает из его определения. То есть мы имеем переменную Т, которая указывает на корень бинарного дерева. А каждый узел имеет две переменные связи: LLink и RLink, которые указывают на левое и правое поддеревья соответственно. Если дерево пусто, то указатель на него равен и. В алгоритмах работы с древовидными структурами наиболее часто встречается понятие обход дерева. При таком методе исследования дерева каждый узел посещается ровно один раз, а полный обход задает линейное упорядочение узлов, что позволяет упростить алгоритм, так как при этом можно использовать понятие следующий узел, т.е. узел, который располагается перед данным узлом в таком упорядочении или после него. Для обхода бинарных деревьев можно применить один из трех

принципиально разных способов: в прямом порядке, в центрированном порядке или в обратном порядке. Эти три метода определяются рекурсивно. Если дерево пусто, то для его обхода ничего делать не нужно, в противном случае обход выполняется в три этапа.

Прямой порядок обхода:

Попасть в корень

Пройти левое поддерево

Пройти правое поддерево

Центрированный порядок обхода:

Пройти левое поддерево

Попасть в корень

Пройти правое поддерево

Обратный порядок обхода:

Пройти левое поддерево

Пройти правое поддерево

Попасть в корень

Эти методы обхода реализуются в компьютере либо с помощью рекурсии,

либо с помощью стека, куда сохраняются указатели на родителей.

Графы - обобобщение структуры деревьев. Граф обычно определяется как некоторое множество точек (называемых вершинами) и некоторое множество линий (называемых ребрами), соединяющих определенные пары вершин. Каждая пара вершин соединяется не больше чем

одним ребром. Граф (свободное дерево) обычно определяется как некоторое множество точек (называемых вершинами) и некоторое множество линий, называемых ребрами, соединяющих определенные пары вершин. Каждая пара вершин соединяется не больше чем одним ребром. Дуга, соединенная с вершиной, называется инцидентной этой вершине. Две вершины называются смежными если существует ребро, соединяющее их. Две дуги называются смежными, если они инцидентны одной и той же вершине.

Алгоритм Дейкстры — пример алгоритма, где "жадность" окупается в том смысле, что если что-то "хорошо" локально, то оно будет "хорошо" и глобально. В данном

случае что-то локально "хорошее" — это вычисленное расстояние от источника к

вершине ш, которая пока не входит в множество S, но имеет кратчайший особый

путь. (Напомним, что особым мы назвали путь, который проходит только через вер-

шины множества S.) Чтобы понять, почему не может быть другого кратчайшего, но

не особого, пути, рассмотрим рис. 6.7. Здесь показан гипотетический кратчайший

путь к вершине w, который сначала проходит до вершины х через вершины множества S, затем после вершины х путь, возможно, несколько раз входит в множество S

и выходит из него, пока не достигнет вершины w.

Но если этот путь короче кратчайшего особого пути к вершине w, то и начальный

сегмент пути от источника к вершине х (который тоже является особым путем) также

короче, чем особый путь к w. Но в таком случае в строке (5) листинга 6.3 при выборе

вершины w мы должны были выбрать не эту вершину1, а вершину х, поскольку D[х]

меньше D[w]. Таким образом, мы пришли к противоречию, следовательно, не может быть другого кратчайшего пути к вершине w, кроме особого. (Отметим здесь определяющую роль того факта, что все стоимости дуг неотрицательны, без этого свойства помеченного орграфа алгоритм Дейкстры не будет работать правильно.) Для завершения обоснования алгоритма Дейкстры надо еще доказать, что D[v],действительно показывает кратчайшее расстояние до вершины и. Рассмотрим добавление новой вершины w к множеству 5 (строка (6) листинга 6.3), после чего происходит пересчет элементов массива D в строках (7), (8) этого листинга; при этом может получиться более короткий особый путь к некоторой вершине и, проходящий через вершину w. Если часть этого пути до вершины w проходит через вершины предыдущего множества S и затем непосредственно к вершине и, то стоимость этого пути,D[w]} + С[w, v], в строке (8) листинга 6.3 сравнивается с D[v]] и, если новый путь

короче, изменяется значение D[v].

Основные определения

Граф задается множеством точек или вершин х1, х2, ..., хn и множеством линий или ребер a1, a2, ... , am, соединяющих между собой все или часть точек. Формальное определение графа может быть дано следующим образом.

Графом называется двойка вида

G = (X, A),

где X = {xi}, i = 1, 2, ..., n – множество вершин графа, A = {ai}, i = 1, 2,... , m – множество ребер графа.

Графы могут быть ориентированными, неориентированными и смешанными (рис. 1.2). Если ребра у множества A ориентированы, что обычно показывается стрелкой, то они называются дугами, и граф с такими ребрами называется ориентированным графом или орграфом (рис. 1.2,а).

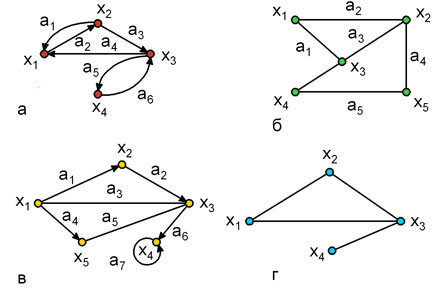
Рис. 1.2.

Если ребра не имеют ориентации, то граф называется неориентированным (рис. 1.2,б). Граф, в котором присутствуют и ребра, и дуги называется смешанным (рис. 1.2,в). В случае, когда G = (X, A) является орграфом, и мы хотим пренебречь направленностью дуг из множества A, то неориентированный граф, соответствующий G, будет обозначаться и называться неориентированным дубликатом или неориентированным двойником (рис. 1.2,г).

Дуга ai может быть представлена упорядоченной парой вершин (хn, хk), состоящей из начальной хn и конечной хk вершин. Например, для графа G1 (рис. 1.2,а) дуга a1 задается парой вершин (x2, x1), а дуга а3 парой (x2, x3). Если хn, хk – концевые вершины дуги ai, то говорят, что вершины хn и хk инцидентны дуге ai или дуга ai инцидентна вершинам хn и хk.

Дуга, у которой начальная и конечная вершины совпадают, называется петлей. В графе G3 (рис. 1.2,в) дуга a7 является петлей.

Каждая вершина орграфа хi может характеризоваться полустепенью исхода d0(хi) и полустепенью захода dt(хi).

Полустепенью исхода вершины хi — d0(хi) называется количество дуг, исходящих из этой вершины. Например, для орграфа G1 (рис. 1.2,а) характеристики полустепеней исхода следующие: d0(х1)=1, d0(х2)=2, d0(х3)=2, d0(х4 )=1.

Полустепенью захода вершины хi — dt(хi) называется количество дуг, входящих в эту вершину. Например, для орграфа G1: dt(х1)=2, dt(х2)=1, dt(х3)=2, dt(х4 )=1.

Очевидно, что сумма полустепеней исхода всех вершин графа, а также сумма полустепеней захода всех вершин графа равна общему числу дуг графа, т. е. ni=1d0(xi)=ni=1dt(xi)=m ,где n – число вершин графа, m – число дуг.

Каждая вершина неориентированного графа хi может характеризоваться степенью вершины d(хi).

Степенью вершины хi – d(хi) называется количество ребер, инцидентных этой вершине. Например, для орграфа G1 (рис. 1.2,б) характеристики степеней следующие: d(х1)=2, d(х2)=3, d(х3)=3, d(х4 )=2.

Способы описания графов

Теоретико-множественное представление графов

Граф описывается перечислением множества вершин и дуг. Примеры описания приведены для орграфов на рис. 1.3 и рис. 1.4.

G4 = (Х, А),

где Х = {хi}, i = 1, 2, 3, 4 – множество вершин; А = {ai }, i = 1, 2, ..., 6 – множество дуг, причем А = {(х1, х2), (х4, х2), (х2, х4 ), (х2, х3), (х3, х3), (х4 , х1)}.

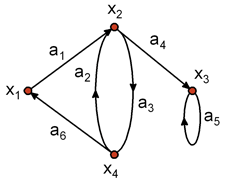
Рис. 1.3.

G5 = (X, A),

где X = {B, C, D, E, F} – множество вершин графа, A = {ai}, i = 1, 2, ..., 5 – множество дуг графа, причем a1 = (F, B), a2 = (B, E), a3 = (F, D), a4 = (E, C), a5 = (C, D).

Рис. 1.4.

Задание графов соответствием Описание графов состоит в задании множества вершин Х и соответствия Г, которое показывает, как между собой связаны вершины. Соответствием Г называется отображение множества Х в Х, а граф в этом случае обозначается парой G = (X, Г).

Отображением вершины хi — Г(хi) является множество вершин, в которые существуют дуги из вершины хi, т. е. Г(хi) = { хj: дуга (хi, хj)A}.

Так для орграфа на рис. 1.3 описание заданием множества вершин и соответствия выглядит следующим образом:

G4=(X, Г),

где X = {хi}, I = 1, 2, ..., 4 – множество вершин, Г(х1) = { х2 }, Г(х2) = { х3, х4 }, Г(х3) = { х3 }, Г(х4) = { х1, х2 } – отображения.

Для неориентированного или смешанного графов предполагается, что соответствие Г задает такой эквивалентный ориентированный граф, который получается из исходного графа заменой каждого неориентированного ребра двумя противоположно направленными дугами, соединяющими те же самые вершины. Например, для графа на рис. 1.2,б Г(х2) = { х1, х3, х5 }, Г(х4) ={ х3, х5} и т. д.