1. Содержание математического программирования. Постановка общей и основной задач линейного программирования

Т ермин математическое программирование предложил математик Дорфман. Содержание МП составляют теория и методы решения задач о нахождении экстремумов функций на множествах, определяемых линейными и нелинейными ограничениями (равенствами и/или неравенствами). Слово "программирование" означает "планирование" или "поиск наилучших планов". МП является одним из разделов науки об исследовании операций.

ЛП является основным разделом МП. К задачам ЛП относятся задачи, в которых требуется найти max или min значение некоторой линейной целевой функции на множестве, определяемом системой линейных равенств или неравенств. В ЛП существует класс задач, структура которого позволяет создать специальные методы их решения, выгодно отличающиеся от методов решения задач общего характера – раздел транспортных задач.

Д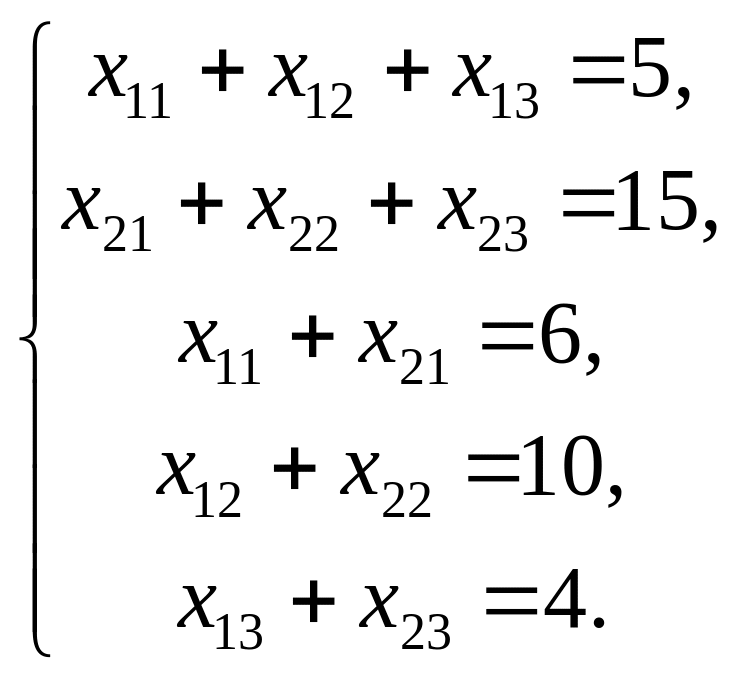 ля практического решения экономической задачи математическими методами прежде всего ее следует записать с помощью математических выражений (уравнений, неравенств), т. е. составить экономико-математическую модель.

Общая схема формирования модели:

1. выбор некоторого числа переменных величин, заданием числовых значений которых однозначно определяется одно из возможных состояний исследуемого явления;

2. выражение взаимосвязей, присущих явлению, в виде математических соотношений, эти соотношения образуют систему ограничений задачи;

3. количественное выражение выбранного критерия оптимальности в форме целевой функции;

4. математическая формулировка задачи как задачи нахождения экстремума целевой функции при условии выполнения ограничений, накладываемых на переменные.

Примеры задач ЛП.

Задача 1. Использование сырья. Предприятие может выпускать два вида продукции (P₁,P₂). На их изготовление расходуется три вида сырья (S₁,S₂,S₃). Запасы сырья, нормы их расхода на единицу изделия a_ij (i = 1,2,3; j = 1,2), себестоимость c_j (j=1,2) и цены приведены в таблице:

Тип сырья	Запас cырья	Нормы расхода сырья на изделие
		P1	P2
S1	100	10	20
S2	120	20	10
S3	140	20	20
Себестоимость, $		5	10
Цены, $		7	13

Требуется составить план выпуска продукции, обеспечивающий получение максимальной прибыли.

Построим математическую модель: обозначим x₁ и x₂ – количество выпускаемой продукции P₁ и P₂. На изготовление изделий P₁, P₂ будет израсходовано 10x₁ + 20x₂ единиц сырья S₁. По условию имеем: 10x₁ + 20x₂  100.

Аналогичным образом получаем ограничения по другим видам сырья:

20x₁ + 10x₂  120,

20x₁ + 20x₂  140.

В результате реализации единицы изделия P₁ предприятие получит прибыль (7–5) = 2 усл. ед.; единицы изделия P₂ – прибыль (13–10) = 3 усл. ед. Общая прибыль составит:

f(x₁,x₂) = 2x₁ + 3x₂ .

Итак, задача свелась к нахождению неотрицательных чисел x₁ и x₂, удовлетворяющих линейным ограничениям и обращающих в максимум линейную целевую функцию f(x₁,x₂).

Задача 2. Транспортная задача. В двух пунктах отправления сосредоточен однородный груз в количестве 5 и 15 т. Груз необходимо доставить трем потребителям, потребности которых таковы: 1-й потребитель – 6 т, 2-й потребитель – 10 т, 3-й потребитель – 4 т. Известны также затраты на перевозку единицы груза из i-го пункта отправления в каждый j-й пункт потребления:

Требуется составить такой план перевозок груза, при котором общая стоимость перевозок была бы минимальной.

Математическая модель: обозначим x_ij – объем перевозок груза из i-го пункта отправления в j-й пункт потребления (i = 1,2; j = 1,2,3). Тогда получим:

F(x) = x₁₁ + 9x₁₂ + 7x₁₃ + 8x₂₁ + 5x₂₂ + 4x₂₃min

при ограничениях