
- •Равенство вещественных чисел
- •Неравенство между рациональными и иррациональными числами
- •Границы числовых множеств
- •Алгебраические операции над вещественными числами
- •Определение: корня
- •Теория пределов
- •Свойства пределов
- •Предельный переход в неравенствах
- •Бесконечные пределы последовательностей
- •Бесконечно большие и бесконечно малые последовательности
- •Предел функции в точке
- •Некоторые существенные неравенства
- •Арифметические свойства непрерывных функций в точке
- •Свойства функций, непрерывных на замкнутом промежутке
- •Производные и ее основные свойства
Бесконечные пределы последовательностей
![]() <=>
A>0
существует
N :
n>N в.н.
xn>A
<=>
A>0
существует
N :
n>N в.н.
xn>A
![]() <=>
B<0
существует
N :
n>N в.н.
yn<B
<=>
B<0
существует
N :
n>N в.н.
yn<B
Свойства:
1 )
)
![]() =>
=>
![]()
![]() =>
=>
![]()
2)
![]() C>0
C>0
![]()
C<0
![]()

 =>
=>
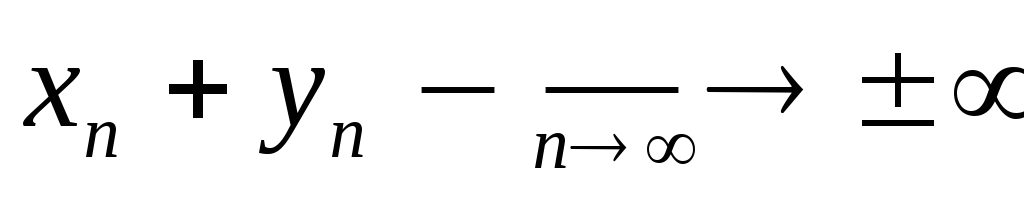
yn ограничена
zn=(-1)n
n не
существует
![]()
Бесконечно большие и бесконечно малые последовательности
Определение:
Последовательность
{xn}
является бесконечно малой (б/м) <=>![]()
Последовательность
{yn}
является бесконечно большой (б/б) в узком
смысле <=>![]()
Последовательность
{yn}
является бесконечно большой (б/б) в
широком смысле <=>![]()
Последовательность
zn=(-1)n
n является
бесконечно большой (б/б) в широком смысле,
т.к.
![]()
Теорема:
Пусть yn0 и является б/б в широком смысле, тогда xn=1/ yn является б/м.
Пусть wn0 и является б/м, тогда zn=1/ wn является б/б в широком смысле
Если wn состоит из чисел одного знака, то zn является б/б в узком смысле
Предел функции в точке
Определение: Пусть существует функция f определенная на (a,b)\{x0} (x0(a,b))
![]() (
(![]() )
<=>
>0
существует
>0
: x(a,b)\{x0}
: |x-x0|<
в.н.
|f(x)-A|<
)
<=>
>0
существует
>0
: x(a,b)\{x0}
: |x-x0|<
в.н.
|f(x)-A|<
Определение: Пусть существует функция g определенная на (a,b)\{x0} (x0(a,b))
![]() (
(![]() )
<=>
L>0
существует
>0
: x(a,b)\{x0}
: |x-x0|<
в.н. g(x)>L
)
<=>
L>0
существует
>0
: x(a,b)\{x0}
: |x-x0|<
в.н. g(x)>L
Определение: Пусть существует функция h определенная на (a,b)\{x0} (x0(a,b))
![]() (
(![]() )
<=>
k>0
существует
>0
: x(a,b)\{x0}
: |x-x0|<
в.н. h(x)<k
)
<=>
k>0
существует
>0
: x(a,b)\{x0}
: |x-x0|<
в.н. h(x)<k
Определение: Пусть существует функция f определенная на (a,b)
![]() (
(![]() )
<=>
>0
существует
>0
: x(a,b)
: a<x<a+
в.н.
|f(x)-A|<
)
<=>
>0
существует
>0
: x(a,b)
: a<x<a+
в.н.
|f(x)-A|<
Определение: Пусть существует функция f определенная на (a,b)
![]() (
(![]() )
<=>
>0
существует
>0
: x(a,b)
: b-<x<b
в.н.
|f(x)-B|<
)
<=>
>0
существует
>0
: x(a,b)
: b-<x<b
в.н.
|f(x)-B|<
Определение: Пусть существует функция g определенная на (a,b)
![]() (
(![]() )
<=>
L>0
существует
>0
: x(a,b)
: a<x<a+
в.н. g(x)>L
)
<=>
L>0
существует
>0
: x(a,b)
: a<x<a+
в.н. g(x)>L
Определение: Пусть существует функция h определенная на (a,b)
![]() (
(![]() )
<=>
k>0
существует
>0
: x(a,b)
: a<x<a+
в.н. h(x)<k
)
<=>
k>0
существует
>0
: x(a,b)
: a<x<a+
в.н. h(x)<k
Определение: Пусть существует функция g определенная на (a,b)
![]() (
(![]() )
<=>
L>0
существует
>0
: x(a,b)
: b-<x<b
в.н. g(x)>L
)
<=>
L>0
существует
>0
: x(a,b)
: b-<x<b
в.н. g(x)>L
Определение: Пусть существует функция h определенная на (a,b)
![]() (
(![]() )
<=>
k>0
существует
>0
: x(a,b)
: b-<x<b
в.н. h(x)<k
)
<=>
k>0
существует
>0
: x(a,b)
: b-<x<b
в.н. h(x)<k
Предел справа или слева, конечный или бесконечный называется односторонним пределом функции.
Некоторые существенные неравенства
![]()
![]()
![]()
![]()
![]()
Замечательные пределы




 ,
r0
,
r0
Определение:
Пусть существует f определенная на (a,b) (x0(a,b)), тогда
Существует предел
![]()
Если функция g
определена на [a,b), то говорят, g непрерывна
в точке а или существует
![]()
Если функция g не непрерывна в точке а, то говорят, что она разрывна в точке а.
Пусть h
определена на (a,b],
то говорят, что h
непрерывна в точке b,
если существует
![]()
Арифметические свойства непрерывных функций в точке
Пусть - любое значение
Пусть f непрерывна в точке , тогда Сf непрерывна в точке .
Пусть f,g непрерывны в точке , тогда f+g непрерывна в точке .
Пусть f,g непрерывны в точке , тогда fg непрерывна в точке .
Пусть f(x)0 x и f непрерывна в точке , тогда 1/f непрерывна в точке .
Пусть f(x)0 x и f,g непрерывны в точке , тогда g/f непрерывна в точке .
Теорема:
П устьf[a,b],
g[a,b],
f непрерывна
в точке ,
f()=
устьf[a,b],
g[a,b],
f непрерывна
в точке ,
f()=
P<=f(x)<=q x[a,b]
Пусть g(y) определена на [p,q] и непрерывна в точке , => h(x) непр.
h(x)=g(f(x))
Лемма:
Пусть f(x) непрерывна в точке <=>
<=>>0 существует >0 : x[a,b] : |x-|< в.н. |f(x)-f(|<
