Определение сечения во множестве рациональных чисел

(Ключевое определение в теории Дедекинда)

Определение: Будем говорить, что во множестве рациональных чисел Q произведено сечение, если Q=АА`, а

АА`

АА`=

rА и r`А` r<r`

При этом множество А называют нижним классом сечения, а

множество А` называют верхним классом сечения.

1. Пусть r₀Q

A состоит из всех rQ : r<=r₀

A` = {r`Q : r`>r₀}

rA, r`A`

r<=r₀<r` => r<r`

В А есть самое большое число т.к. r₀ <=r₀ => r₀A

В А` нет самого маленького числа.

Доказательство:

Лемма о плотности множества Q

Пусть r₁,r₂Q : r₁<r₂ => существует rQ : r₁<r<r₂

Доказательство: 1) r₁<0, r₂>0 => r=0

2) r₁,r₂<0 => r= (r₁+r₂)/2

Доказательство от противного:

rA, r`A`

Пусть r₁`A`, r₁`<=r` r`A`

r₁`>r<sub>0</sub>, т.к. r<sub>1</sub>`A` по Лемме существует r<sub>2</sub>Q : r<sub>0</sub><r<sub>2</sub><r<sub>1</sub>`

r₂>r₀ => r₂A и r₂<r₁` => r<sub>2</sub>A` => r₂AА` <=> АА`Q <=> r₂Q

Значит наше предположение неверно, в А нет самого маленького числа.

2. Пусть r0q

A = {rQ : r<r₀}

A` = {r`Q : r`>=r₀}

В А нет самое большого число

В А` есть самого маленькое числа.

3. A = {rQ : r<=0 или rQ : (r>0)r²<2)}

A` = {r`Q : (r`>0)r`²>2)}

Лемма Не существует r₀Q : r₀²=2

Доказательство:

Пусть существует r₀Q : r₀²=2

Пусть r₀²= |r₀|² т.к. r₀Q

т.е. т.е. т.е.

p₀=2p₁

q₀=2q₁

Значит наше предположение не верно, не существует r₀Q : r₀²=2

Данная лемма rQ выполняется неравенство r²<2)r²>2)

Таким образом получает сечение рациональных чисел.

В полученном сечении В А нет самое большого число

В А` нет самого маленького числа.

Свойство полученного сечения.

В верхнем классе А нет самое большого число

В нажнем классе А` нет самого маленького числа.

Пусть 0<r=p/q ,p,qN

p>=1, q>=1

r₁=

r₁A т.к. r₁² >2 ; r₁>r

Значит в нижнем классе нет наибольшего числа.

Для верхнего класса доказательство аналогично.

Сечение которое показано в 3-ем примере, как будет формально записано позднее задает иррациональное число 2

Основное утверждение о сечениях множества рациональных чисел.

Утверждение: Пусть сечение А,А`. Тогда не может произойти так, чтобы в нижнем классе А было максимальное число, а в верхнем А` минимальное число.

Доказательство:

Пусть верно обратное т.е.

Существует r₀A : rA r<= r₀ и

Существует r₁`A` : r`A` r`>= r<sub>1</sub>`

r₀<r₁` (по 3-му свойству сечений) => существует Q : r<sub>0</sub><<r<sub>1</sub>`

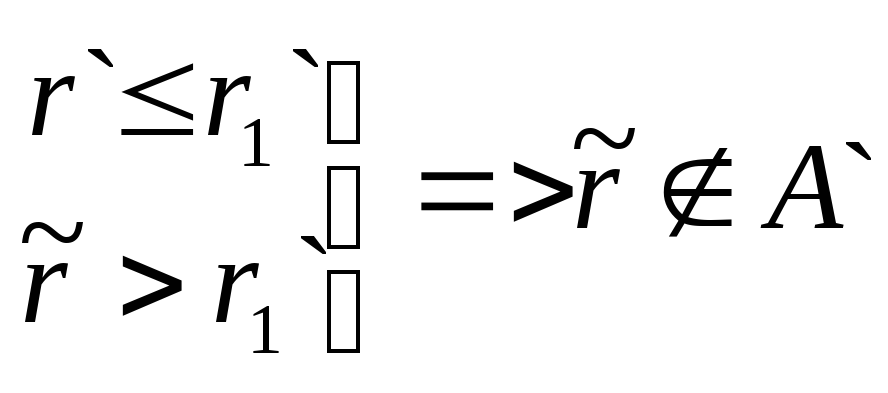=>  АА`=Q

Значит наше предположение неверно

Следствие в Q

Пусть существует А,А` тогда:

• либо в А есть наибольшее, а в А` нет наименьшего числа

• либо в А` есть наименьшее, а в А нет наибольшего числа

• либо в А нет наибольшего, а в А` нет наименьшего числа

Доказательство

	Есть	Нет			Есть	Нет			Есть	Нет			Есть	Нет
А	1	0		А	1	0		А	0	1		А	0	1
А`	1	0		А`	0	1		А`	0	1		А`	1	0

Невозможно

Определение: Пусть есть произвольное сечение множества Q. Если для него выполняется 1 или 2 утверждение следствия, то говорят, что это сечение определяет именно то число Q, которое является либо наибольшим в нижнем классе, либо наименьшем в верхнем классе.

Если для него выполняется третье утверждение следствия, то оно определяет некоторое иррациональное число.

Определение: Множество всех рациональных чисел и множество всех иррациональных чисел называется множество вещественных чисел Q+I=R

Равенство вещественных чисел

Считается, что никакое рациональное число не равняется никакому иррациональному числу.

Пусть существует сечение А,A` и А<sub>1</sub>, А<sub>1</sub>` во множестве иррациональных чисел.

Иррациональные числа определяемые сечениями А,A` и А<sub>1</sub>, А<sub>1</sub>` называют равными, если А=А₁ А`=А<sub>1</sub>` => А=А₁ А`=А<sub>1</sub>`, т.к. А определяет А` и А` определяет А.

Неравенство между рациональными и иррациональными числами

Пусть есть иррациональное число определенное сечением А,A` ( и пусть есть произвольное рациональное число.

Пусть r₀Q r₀< <=> > r₀<=> r₀A

Пусть r₁Q r₁> <=>  r₁<=> r₁A`

Неравенство между иррациональными числами.

Пусть есть сечение А,A`) и есть сечение  (B,B`)

Утверждение о множествах А и В

При указанных подмножествах чисел А, В могут существовать три возможности.

1. АB, AB

2. A=B

3. , BA

Определение: Если выполнено 1) то говорят, что 

2) то говорят, что 

3) то говорят, что 

Теорема: Для неравенств между вещественными числами справедливы свойства неравенств, применяемых для рациональных чисел.

Представление вещественных чисел в виде десятичных дробей.

Q₁₀ множество состоящее из чисел вида p/10^m , pZ, mN

rQ, rQ₁₀

Существует единственное mZ : m<r<m+1

Если и т.д. m₁0,1,2..9

r существует m_к :

(m, m₁, m₂, …)

То же для I : m<m+1 существует m₁0,1,2..9 : .

Определение: Будем говорить, что в множестве R проведено сечение, если R= АА`, причем А и А` обладают следующими свойствами

1) АА`

2) АА`=

rА и r`А` r<r`

множество А нижний класс сечения

множество А` верхний класс сечения

Теорема Дедекинда.

Для всякого сечения АА` в области вещественных чисел существует вещественное число , которое производит это сечение. Это число будет

1. Либо наибольшим в нижнем классе А

2. Либо наименьшим в верхнем классе А`

Доказательство:

1) В А нет наибольшего, в А` нет наименьшего.

Пусть верно обратное, т.е.

Существует ₁A` : `A` <sub>1</sub><=`, существует ₀A : A <=₀

По третьему свойству ₀<₁`

Пусть ₀,₁`I, тогда <sub>0</sub><<sub>1</sub>` <=> C₀С₁ и C₀С₁

Существует rQ : rС₁ <=> r<₁`, rС₀ <=> rС₁ <=> r>₀

Получаем: Существует rQ : r>₀ => rA

r<₁` => rA` => rАА` => rQ !!

Значит наше предположение неверно: В А нет наибольшего, в А` нет наименьшего.

2) А, А`R

V=AQ V,V`Q

V`=A`Q

₀R тогда ₀A или ₀A`

Пусть ₀A => A выполняется неравенство ₀

Пусть верно обратное, т.е. не наибольшее в А, т.е. существует ^*A : ^*>₀

Существует r₀Q : ₀<r₀<^*

^*A => r₀A и r₀Q => r₀ V

r₀ V, ₀ определяется сечением V,V` =>

r₀<=₀ => значит наше предположение неверно ₀A =>

но r₀>₀ A выполняется неравенство ₀

Для ₀A` доказательство аналогичное.