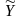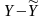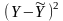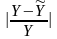4. А) оценка тесноты связи показателей парной линейной регрессии.
Для оценки тесноты связи рассчитаем линейный коэффициент парной корреляции. Он вычисляется по формуле
.
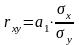Найдем средние квадратические отклонения признаков:
;
.
.
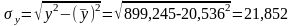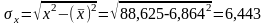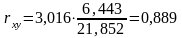Коэффициент корреляции находится в промежутке от 0,7 до 0,9, что показывает наличие тесной связи между признаками. Положительное значение коэффициента корреляции (как и коэффициента регрессии) показывает, что связь прямая.
Коэффициент детерминации в случае линейной зависимости равен квадрату коэффициента корреляции:
.
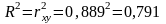Коэффициент детерминации показывает, что 79,1% вариации результативного признака Y (объем ВРП) объясняется изменением признака-фактора X (инвестиции в основной капитал). Остальные 20,9% вариации приходятся на долю прочих факторов, не учтенных в уравнении регрессии.
б) оценка тесноты связи показателей парной логарифмической регрессии.
Для дальнейших вычислений понадобится еще одна расчетная таблица.
Таблица 1.5
№ |
Y |
X |
|
|
|
|
1 |
4,3 |
0,610 |
-6,320 |
10,620 |
112,777 |
263,620 |
2 |
2,0 |
0,930 |
-0,149 |
2,149 |
4,618 |
343,597 |
3 |
5,1 |
1,264 |
4,341 |
0,759 |
0,576 |
238,281 |
4 |
7,6 |
1,600 |
7,790 |
-0,190 |
0,036 |
167,350 |
5 |
10,5 |
2,382 |
13,612 |
-3,112 |
9,687 |
100,729 |
6 |
13,0 |
3,344 |
18,576 |
-5,576 |
31,090 |
56,797 |
7 |
2,1 |
6,689 |
28,720 |
-26,620 |
708,625 |
339,900 |
8 |
50,0 |
10,936 |
35,913 |
14,087 |
198,445 |
868,106 |
9 |
18,9 |
12,633 |
38,024 |
-19,124 |
365,712 |
2,678 |
10 |
43,4 |
15,104 |
40,638 |
2,762 |
7,631 |
522,746 |
11 |
69,0 |
20,014 |
2,996 |
206,754 |
4761,00 |
8,979 |
∑ |
69,0 |
20,014 |
44,756 |
24,244 |
587,772 |
2348,724 |
- теоретические значение, рассчитанные по уравнению регрессии .
Найдем коэффициент детерминации:
.
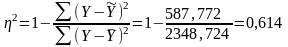Коэффициент детерминации показывает, что 61,4% вариации результативного признака Y (объем ВРП) объясняется изменением признака-фактора X (инвестиции в основной капитал).
Коэффициент
корреляции:
.
Значение коэффициента корреляции находится в пределах от 0,7 до 0,9, следовательно, связь между объемом ВРП и инвестициями в основной капитал тесная.
5. Оценим качество уравнения с помощью f-критерия Фишера.
F-критерий Фишера заключается в следующем:
Выдвигается
нулевая гипотеза
о том, что коэффициент детерминации
равен 0, и уравнение регрессии статистически
малозначимо и ненадежно. Альтернативная
ей гипотеза
будет заключаться в том, что коэффициент
детерминации отличен от 0, т.е. связь
между X
и
Y
статистически
значима, и уравнение регрессии качественно
описывает эту взаимосвязь.
Вычисляется наблюдаемое значение критерия по формуле
.
Находим:
Для
линейной регрессии:
;
Для
логарифмической регрессии:
.
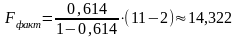По
таблице значений F-критерия
Фишера при уровне значимости α=0.05 и
степенях свободы
,
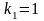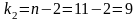получаем
.
Оба наблюдаемых значений F-критерия превышает табличное, а значит, в обоих случаях нулевая гипотеза H0 о случайной природе полученного уравнения регрессии отвергается в пользу гипотезы H1, свидетельствующей в 95% случаев о статистической значимости и адекватности уравнений регрессий. В первом случае факторная вариация в 34 раза превышает остаточную, во втором случае – только в 14,3 раз. Подобные различия не могут быть случайными, а являются результатом систематического взаимодействия валового регионального продукта и размером инвестиций.
6. Поскольку коэффициенты корреляции, детерминации, а также F-статистика в случае линейной регрессии выше соответствующих показателей для логарифмической регрессии, то лучшим уравнением является уравнение парной линейной регрессии.
7.
По уравнению линейной регрессии определим
теоретические значения результативного
признака (
),
отклонения фактических значений от
теоретических (
)
и вычислим среднюю ошибку аппроксимации
(
).
Таблица 1.6
№ |
Y |
X |
|
|
|
|
|
1 |
4,3 |
0,610 |
1,674 |
2,626 |
6,896 |
0,611 |
39,1 |
2 |
2,0 |
0,930 |
2,639 |
-0,639 |
0,409 |
0,320 |
35,2 |
3 |
5,1 |
1,264 |
3,646 |
1,454 |
2,113 |
0,285 |
31,4 |
4 |
7,6 |
1,600 |
4,660 |
2,940 |
8,645 |
0,387 |
27,7 |
5 |
10,5 |
2,382 |
7,018 |
3,482 |
12,122 |
0,332 |
20,1 |
6 |
13,0 |
3,344 |
9,920 |
3,080 |
9,489 |
0,237 |
12,4 |
7 |
2,1 |
6,689 |
20,008 |
-17,908 |
320,697 |
8,528 |
0,0 |
8 |
50,0 |
10,936 |
32,817 |
17,183 |
295,263 |
0,344 |
16,6 |
9 |
18,9 |
12,633 |
37,935 |
-19,035 |
362,326 |
1,007 |
33,3 |
10 |
43,4 |
15,104 |
45,387 |
-1,987 |
3,949 |
0,046 |
67,9 |
11 |
69,0 |
20,014 |
60,196 |
8,804 |
77,517 |
0,128 |
172,9 |
∑ |
225,9 |
75,506 |
225,900 |
0,000 |
1099,425 |
12,222 |
456,587 |
Фактические значения и теоретическая линия регрессии представлена на рис 1.2.
Средняя ошибка аппроксимации:
.
Средняя ошибка аппроксимации достаточно велика, т.е. фактические и теоретические значения различаются существенно.
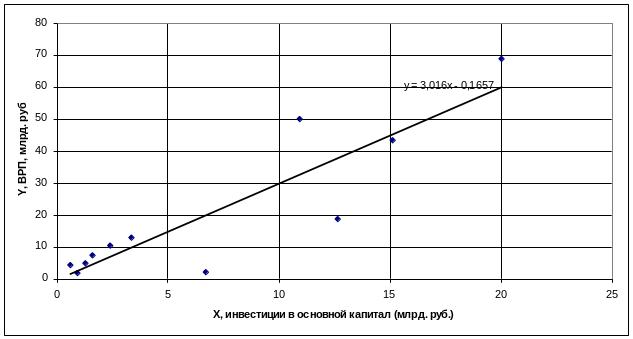
Рис. 1.2. Фактические значения и теоретическая линия регрессии
8. По полученному уравнению регрессии выполним прогноз.
Определим значение фактора X, которое составит 1,062 от среднего значения:
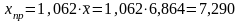(млрд.
руб.)
Тогда находим прогнозное значение Y:
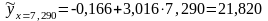(млрд.
руб.)
Таким образом, если объем инвестиций будет равен 7,290 млрд. руб., ожидаемое значение ВРП составит 21,820 млрд. руб.
9. Стандартная ошибка прогноза определяется по формуле
.
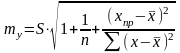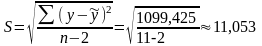(млрд.
руб.)
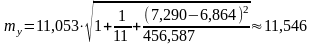(млрд.
руб.)
При доверительной вероятности 95% t=1.96. Определим доверительный интервал прогноза:
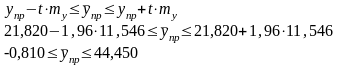
Диапазон верхней и нижней границ интервала:
(млрд.
руб.)
Относительная
погрешность:
.
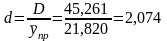Вывод: если размер инвестиций составит 7,290 млрд. руб., ВРП с вероятностью 95% будет не более 44,450 млрд. руб. Интервал прогноза весьма велик (в 2 раза больше предсказанного значения), так что точность прогноза невысокая.