45. Барометрическая формула.Распределение Больцмана.

На молекулы газа внешние силы не действуют,поэтому молекулы равномерно распределены по объему.Однако молекулы газа(например,воздуха)находятся в потенциальном поле Земли.Тяготение,с одной стороны,и тепловое движение-с другой,приводят к тому,что давление газа с высотой убывает по закону

p=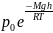 – барометрическая формула,где 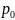-давление на высоте,соответствующей уровню моря,е=2,7.

p= = 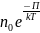– распределение Больцмана,где n-концентрация молекул газа на высоте h, -концентрация молекул газа на высоте h=0;П=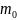 gh-потенциальная энергия молекулы в поле тяготения.Из формулы видно,что при постоянной температуре концентрация газа убывает с высотой,т.е.больше там,где меньше потенциальная энергия его молекул. k=1,38∙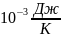

Плотность энергии электростатического поля

W=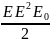 ,где E=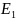 + ,т.к.векторы напряженности между зарядами и направлены в одну сторону.

48. Закон Джоуля – Ленца в интегральной и дифференциальной формах.

Если в проводнике течет постоянный ток и проводник остается неподвижным, то работа сторонних сил расходуется на его нагревание. Опыт показывает, что в любом проводнике происходит выделение теплоты, равное работе, совершаемой электрическими силами по переносу заряда вдоль проводника. Если на концах участка проводника имеется разность потенциалов , тогда работу по переносу заряда q на этом участке равна

По определению I= q/t. откуда q= I t. Следовательно

Так как работа идет па нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил (17.13)

Соотношение (17.13) выражает закон Джоуля-Ленца в интегральной форме. Введем плотность тепловой мощности , равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника

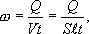
где S - поперечное сечение проводника, - его длина. Используя (1.13) и соотношение , получим

Но - плотность тока, а , тогда

с учетом закона Ома в дифференциальной форме , окончательно получаем

(17.14)

Формула (17.14) выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.

6. Теорема Остроградского-Гаусса для напряженности электрического поля в вакууме.

Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. Применяется отдельно для вычисления электростатических полей.

Теорема Гаусса для напряжённости электрического поля в вакууме

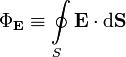поток вектора напряжённости электрического поля через замкнутую поверхность

полный заряд, содержащийся в объёме, который ограничивает поверхность .

• — электрическая постоянная.

Средняя длина свободного пробега молекул

Молекулы газа имеют конечные размеры и при тепловом движении непрерывно соударяются друг с другом. Между двумя последовательными соударениями молекулы, двигаясь равномерно и прямолинейно, проходят некоторые расстояния, называемые длинами свободных пробегов λ. Средней длиной свободного пробега называется среднее расстояние, которое молекула проходит без столкновений.

формула для средней длины свободного пробега

Для идеального газа ;