39 Закон вязкого трения, теплопроводности и диффузии в газах

Ньютон предположил, что величина этой силы (сила внутреннего трения) пропорциональна разности скоростей элементов жидкости. Закон вязкого трения Ньютона гласит, что сила внутреннего трения F пропорциональна изменению скорости жидкости v в направлении, перпендикулярном движению, и зависит от площади S соприкосновения элементов жидкости. Коэффициент пропорциональности в нём называется коэффициентом динамической вязкости (η).

Жидкости, в которых внутреннее трение подобным образом зависит от изменения скорости, называются жидкостями с линейной вязкостью, или ньютоновскими жидкостями. В более строгой формулировке линейная зависимость вязкого трения от изменения скорости движения жидкости называется уравнением Навье-Стокса. Оно учитывает сжимаемость жидкостей и газов и справедливо не только вблизи поверхности твёрдого тела, но и в каждой точке жидкости.

Теплопрово́дность — это перенос тепловой энергии структурными частицами вещества (молекулами, атомами, ионами) в процессе их теплового движения. Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества.

В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиенту температуры:

где  — вектор плотности теплового потока — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси,  — коэффициент теплопроводности (иногда называемый просто теплопроводностью),  — температура. Минус в правой части показывает, что тепловой поток направлен противоположно вектору grad T (то есть в сторону скорейшего убывания температуры). Это выражение известно как закон теплопроводности Фурье.^[1]

В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):

где  — полная мощность тепловых потерь,  — площадь сечения параллелепипеда,  — перепад температур граней,  — длина параллелепипеда, то есть расстояние между гранями.

Коэффициент теплопроводности измеряется в Вт/(м·K).

Диффузия (лат. diffusio — распространение, растекание, рассеивание, взаимодействие) — процесс взаимного проникновения молекул одного вещества между молекулами другого, приводящий к самопроизвольному выравниванию их концентраций по всему занимаемому объёму^[1]. В некоторых ситуациях одно из веществ уже имеет выравненную концентрацию и говорят о диффузии одного вещества в другом. При этом перенос вещества происходит из области с высокой концентрацией в область с низкой концентрацией (против градиента концентрации)

Примером диффузии может служить перемешивание газов (например, распространение запахов) или жидкостей (если в воду капнуть чернил, то жидкость через некоторое время станет равномерно окрашенной). Другой пример связан с твёрдым телом: атомы соприкасающихся металлов перемешиваются на границе соприкосновения. Важную роль диффузия частиц играет в физике плазмы.

Обычно под диффузией понимают процессы, сопровождающиеся переносом материи, однако иногда диффузионными называют также другие процессы переноса: теплопроводность, вязкое трение и т. п.

С точки зрения термодинамики движущим потенциалом любого выравнивающего процесса является рост энтропии. При постоянных давлении и температуре в роли такого потенциала выступает химический потенциал µ, обуславливающий поддержание потоков вещества. Поток частиц вещества пропорционален при этом градиенту потенциала

~

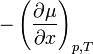
В большинстве практических случаев вместо химического потенциала применяется концентрация C. Прямая замена µ на C становится некорректной в случае больших концентраций, так как химический потенциал связан с концентрацией по логарифмическому закону. Если не рассматривать такие случаи, то вышеприведённую формулу можно заменить на следующую:

которая показывает, что плотность потока вещества J [ ] пропорциональна коэффициенту диффузии D [( )] и градиенту концентрации. Это уравнение выражает первый закон Фика (Адольф Фик — немецкий физиолог, установивший законы диффузии в 1855 г.). Второй закон Фика связывает пространственное и временное изменения концентрации (уравнение диффузии):

Коэффициент диффузии D зависит от температуры.

8 . Применение теоремы Островского –Гауса для расчета напряженности электростатических полей(поле бесконечной равномерно заряженной плоскасти)

       31.Кристаллическое состояние вещества

. Твердыми называют, , тела кристаллического строения, закономерности расположения атомов в которых в значительной мере определяют их свойства. Частицы вещества, находящегося в кристаллическом состоянии, имеют устойчивое положение и располагаются упорядоченно, образуя пространственную кристаллическую решетку. Строение этой решетки, легко определяемое в настоящее время рентгенографически, в большинстве случаев тесно связано с химическим составом вещества.чем проще химический состав тела, тем выше симметрия его кристаллов. 50% элементов и около 70% бинарных соединений образуют, например, кубические кристаллы, 75—85% соединений с четырьмя — пятью атомами в молекуле — гексагональные и ромбические кристаллы и около 80% сложных органических соединений — ромбические и моноклинные кристаллы. Все это можно объяснить тем, что чем однороднее составные части кристаллической решетки, тем более упорядоченно они могут располагаться в пространстве.Важной особенностью кристаллического состояния вещества является его анизотропия, заключающаяся в различии физических свойств химически однородного кристалла в разных его направле-ниях. Анизотропию можно наблюдать на механических, оптических, диффузионных, тепловых и электрических свойствах кристаллических тел. Она проявляется, между прочим, в различной скорости роста кристалла по разным направлениям, в соответствии с чем одни его грани получают большее развитие, чем другие.Структурные элементы, составляющие кристалл, и силы взаимодействия между ними могут быть различными. Соответственно этому различают решетки ионные, молекулярные, ковалентные и металлические.