10. Алгебраический критерий устойчивости дискретных систем

Система называется устойчивой, если ее реакция на кратковременное воздействие при t, стремящемся к бесконечности, будет стремиться к нулю

Передаточная функция:

Корни характеристического уравнения:

.

Это уравнение имеет бесконечное количество корней, однако в полосе частот от до , где ,, число корней характеристического уравнения равно n.

Устойчивость системы определяется положением корней характеристического уравнения на комплексной плоскости.

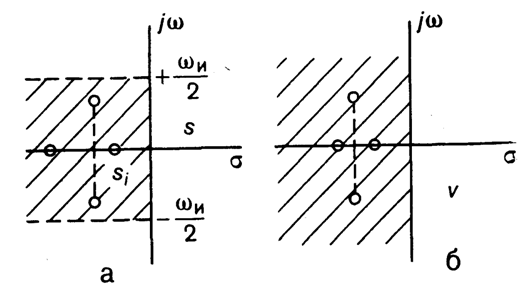
Когда все корни находятся в заштрихованной левой полосе, т. е. имеют отри­цательные вещественные составляющие, то система устойчива. Если хотя бы один корень имеет положительную вещественную составляющую, то система неустойчива. Если один или несколько корней расположены на мнимой оси, то система находится на границе устойчивости.

Чтобы применить к дискретной системе критерий Гурвица, необходимо ввести новую комплексную переменную характеристического многочлена, при которой заштрихованная полуполоса превратится в левую полуплоскость. Этому условию удовлетворяет подстановка:

Тогда характеристическое уравнение может быть записано в следующем виде:

a₀=0.

Приведем это выражение к общему знаменателю:

)ⁿ=0

Сгруппируем:

a₀(1-v)ⁿ=0.

К этому уравнению и следует применять критерий устойчивости Гурвица.

Определитель Гурвица имеет вид:

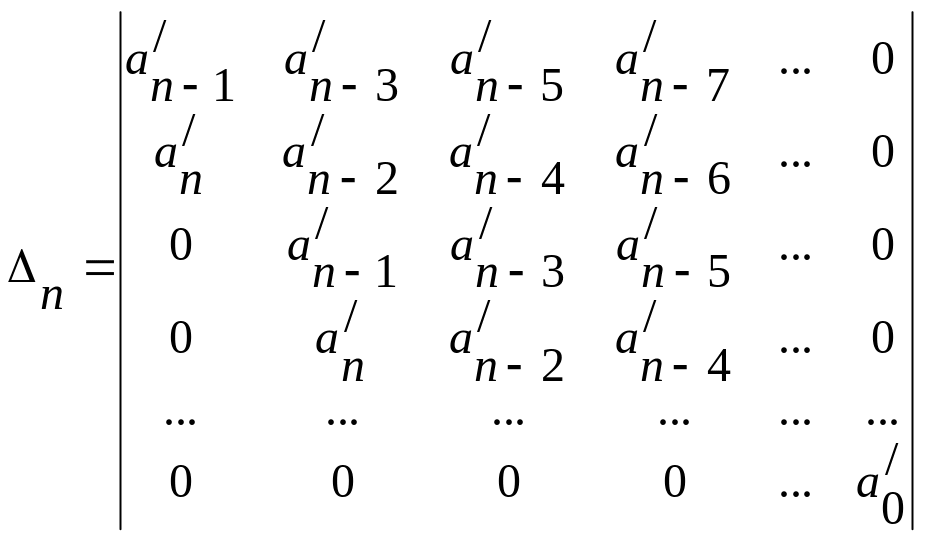
В устойчивой системе все диагональные миноры определителя Гурвица должны быть положительными.

11. Частотный критерий устойчивости дискретных систем

Рассмотрим характеристическое уравнение:

Оно имеет n корней, поэтому в соответствии с теоремой Безу его можно представить в виде:

z - z_n),,

где _zi – корни характеристического уравнения.

Введя переменную , получим:

^И- z_n),

Так как

sinωT_И,

то при изменении частоты от 0 до  угол поворота вектора e^jωTи - z_i будет также равен .

В устойчивой системе угол поворота вектора

равен сумме углов поворота векторов-сомножителей e^jωTи - z_i поэтому

где n – число корней.

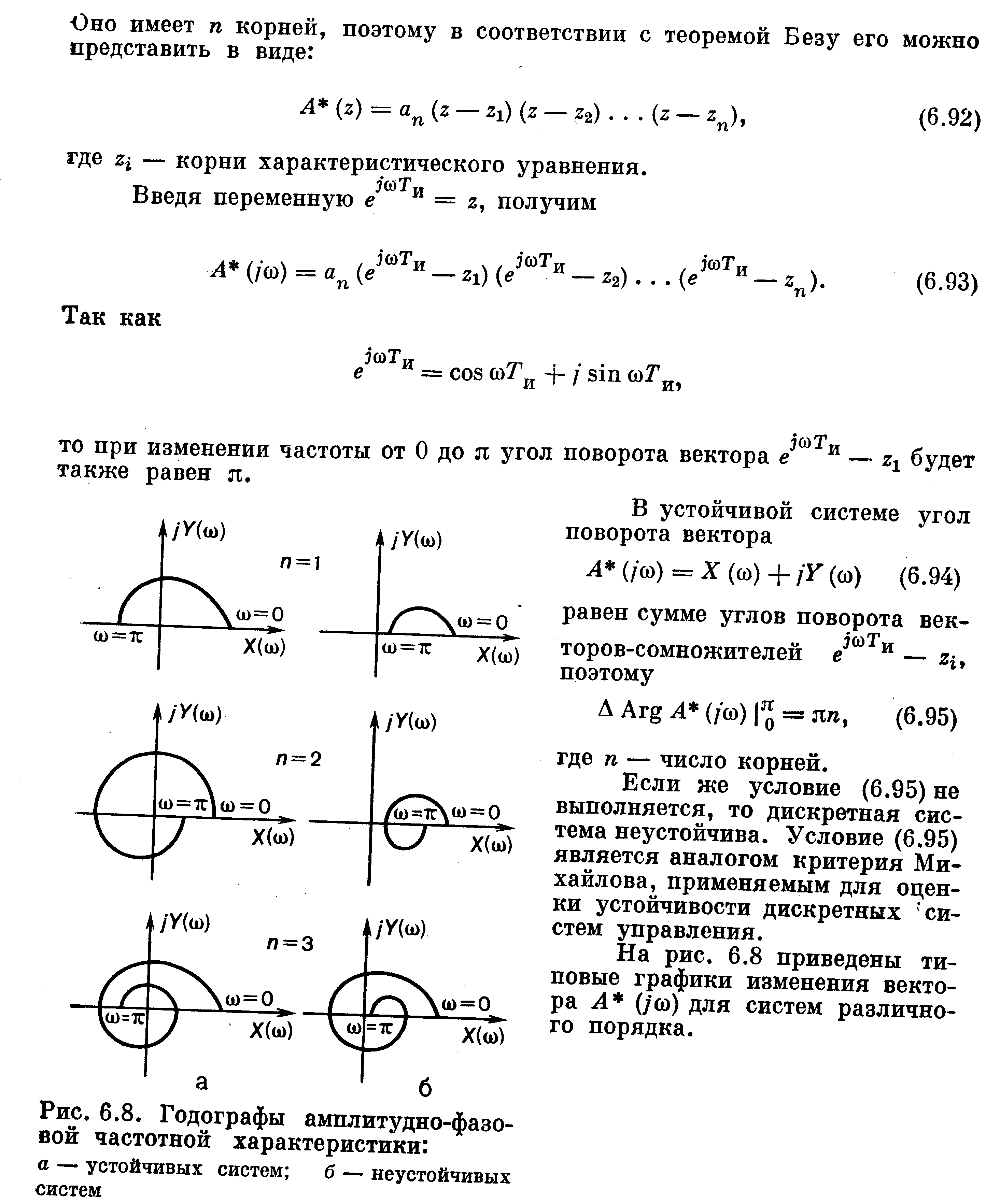
Если же это условие не выполняется, то дискретная система неустойчива. Условие является аналогом критерия Михайлова, применяемым для оценки устойчивости дискретных систем управления. На рис. приведены типовые графики изменения вектора А*(j) для систем различного порядка.

б

Рис. Годографы амплитудно-фазовой частотной характеристики: а-устойчивых систем(3 рисунка), б-неустойчивых(3 рисунка).

12. Метод гармонич линеариз нелин систем

(Б. П. Попов) Рассмотрим нелинейную систему, состоящую из нелинейного элемента и линейной части с комплексным коэффициентом передачи .

При подаче на вход нелинейного элемента гармонического система сигнала x(t) сигнал на его выходе y(t) состоит из бесконечного множества гармоник. При преобразовании сигнала y(t) линейной частью системы амплитуды высокочастотных гармоник существенно уменьшаются и могут стать пренебрежимо малыми по сравнению с амплитудой основной гармоники.

В зависимости от частоты основной гармоники сигнала одна и та же линейная система может обладать и не обладать фильтрующим свойством. В том случае, когда линейная часть системы обладает фильтрующим свойством, при анализе нелинейной системы в целом можно упитывать только одну гармонику сигнала на выходе нелинейного элемента. Это означает, что реальная нелинейная характеристика приближенно заменяется линейной моделью:

, где q и – коэффициенты линеаризации; – частота основной гармоники сигнала. При этом сигнал на выходе нелинейного элемента представляется в виде одной гармоники:

cosω₀t,

где a₁ и b₁ – коэффициенты разложения периодического сигнала на выходе нелинейного элемента в ряд Фурье.