1. Коммутативное (перемест-е) св-во.
Для любых натур-х чисел a и b верно рав-во a+b=b+a.
Теоретико-множ. смысл:
a=n(A), b=n(B)
A∩B=Ø
a+b=n(AUB)=n(BUA)=b+a
Т.к. объед-е мн-в подчиняется коммутат-му св-ву, то n(AUB)=n(BUA).
2. Ассоциативное (сочетат-е) св-во.
Для любых натур-х чисел a, b и с верно рав-во (a+b)+с=a+(b+c).
Теоретико-множ. смысл:
a=n(A), b=n(B), с=n(С)
A∩B=Ø, B∩C=Ø, A∩C=Ø
(a+b)+c=n((AUB)UC)
Т.к. (AUB)UC=AU(BUC), то n((AUB)UC)=n(AU(BUC))=a+(b+c) => (a+b)+c=a+(b+c)
Назначение св-в слож-я заключ-ся в том, чтобы обосновывать те преобраз-я, кот. вып-ся уч-ся нач. шк. при вычислении.
Пример:
1) 1+8=8+1=9 (1 кл.)
2) 20+38=20+(30+8)=(20+30)+8=50+8=58
Словесные формулировки:
От перестановки мест слаг-ых сумма не меняется.
По системе Эльконина-Давыдова сочетат-е св-во слож-я и умнож-я – в виде рав-ва.
Примеры заданий: задания на нахождение суммы.
У Алисы было 2 яблока, у Коли было 3 яблока. Ск-ко всего было яблок?
11. Опред-е вычит-я натур-х чисел через слож-е. Теоретико-множ. смысл разности натур-х чисел. Условие существ-я разности на мн-ве натур-х чисел. Правила вычит-я числа из суммы и суммы из числа, их теоретико-множ. интерпретация. Примеры заданий из нач. курса матем-ки, раскрывающих теоретико-множ. смысл разности натур-х чисел.
В аксиоматич. теории вычит-е натур-х чисел было определено как операция, обратная слож-ю.
Разностью целых неотриц-х чисел a и b назыв-ся такое неотриц-ое число c, что a=b+c.
Теоретико-множ. смысл.
Пусть: a=n(A); b=n(B); BCA (B – подмн-во мн-ва A).
Тогда a-b=n(A\B) (дополнение мн-ва B до мн-ва A).
С теоретико-множ. позиции разность натур-х чисел a и b представ-т собой число эл-тов в доп-ии мн-ва В до мн-ва А.
Напр.: 3-1=2 т.к. 2+1=3
Для того, чтобы разность натур-х чисел a и b существовала на мн-ве натур-х чисел нбх. и достаточно, чтобы a>b.
На мн-ве целых неотриц-х чисел нбх. и достаточно, чтобы a≥b.
I. Правила вычит-я числа из суммы.
Для того, чтобы (a+b)-c достаточно:
1) если a≥c, то (a+b)-c=(a-c)+b.
2) если b≥c, то (a+b)-c=(a+b)-c.
3) если a≥c и b≥c, то верно и 1 и 2.
Для того, чтобы из суммы чисел вычесть некот-е число, достат-о вычесть это число из одного из слагаемых и к получ-му рез-ту прибавить 2ое слаг-е.
Теоретико-множ. обосн-е:
Пусть a=n(A), b=n(B), c=n(C), A∩B=Ø, CCA.
(a+b)-c=n((AUB)\C)
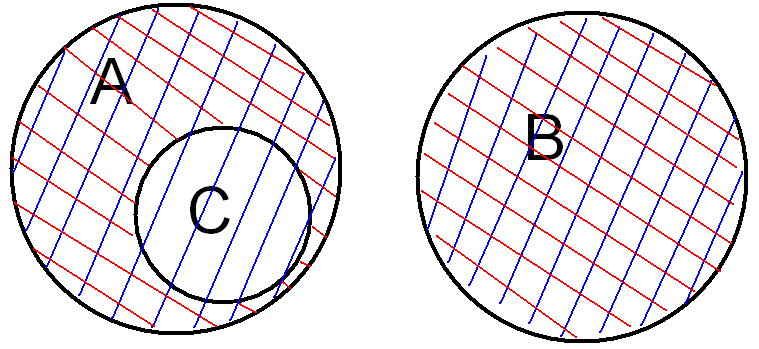
(a-c)+b=n((A\C)UB)
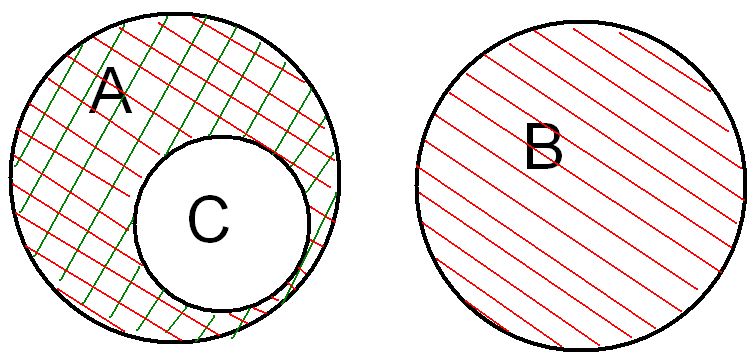
=> (AUB)\C=(A\C)UB => n((AUB)\C)=n((A\C)UB) => (a+b)-c=(a-c)+b
II. Правило вычит-я суммы из числа.
a ≥ b+c => a-(b+c)=(a-b)-c
a-(b+c)=n(A\(BUC))
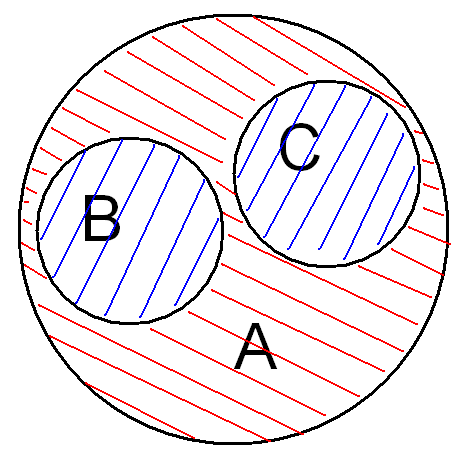
(a-b)-c=n((A\B)\C)
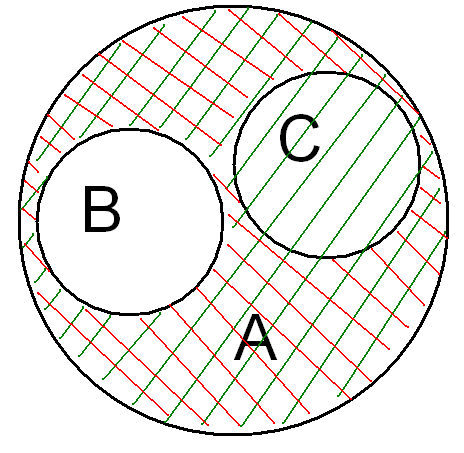
Примеры заданий:
1) У Карлсона было 6 конфет, 5 из кот. он не удержался и съел. Ск-ко у него осталось конфет?
Мн-во конфет – 6.
Подмн-во конфет, которые он съел – 5.
Нбх. найти число эл-тов в доп-нии указанного подмн-ва до данного мн-ва, поэтому данная задача решается при помощи действия вычитания.
2) На столе 5 чашек, а ложек на 2 меньше. Ск-ко на столе ложек?
12. Опред-е умнож-я натур-х чисел через слож-е. Теоретико-множ. смысл произвед-я. Св-ва умнож-я и теоретико-множ. интерпретация. Словесные формулировки св-в умнож-я, изуч. в нач. шк. Примеры заданий из нач. курса матем-ки, раскрывающих теоретико-множ. смысл умнож-я натур-х чисел.
Рез-том действия умнож-я явл-ся произвед-е.
Произвед-ем целых неотриц-х чисел а и b назыв-ся такое целое неотриц-ое число a•b, кот. удовлетворяет след-им усл-ям:
1) если b>1 => a•b=a+a+…+a (b раз);
2) если b=1 => a•1=a;
3) если b=0 => a•0=0.
Напр.:
3•4=3+3+3+3=12
3 – слагаемое
4 – кол-во раз
5•1=5 (по опред-ю)
2•0=0 (по опред-ю)
Теорема: Если b>1, то произвед-е чисел a и b равно сумме b слагаемых, каждое из кот-х равно a.
Теоретико-множ. смысл произвед-я.
Пусть а – натур-е число, число эл-в в b попарно непересек-ся равномощ-х м-у собой мн-в.
a=n(A1)=n(А2)=…=n(Ab)
A1, A2, …, Ab – попарно непересек-ся равномощ. м-у собой мн-ва.
Тогда a•b=n(A1UA2U…UAb)
a•b представляет собой число эл-тов в объединении b мн-в, каждое из кот-х содержит по a эл-тов и никакие 2 из них не пересек-ся.
Опред-е произвед-я целых неотриц-х чисел через декартово умнож-е мн-в:
a•b=n(A×B)
Пусть А и В конечные мн-ва, a=n(A) и b=n(B). Тогда их декартово произвед-е также явл-ся конечным мн-вом, причем n(A×B) = n(A)×n(B).
Декарт-ым произв-ем мн-в A и B назыв-ся мн-во всех пар, первая компонента кот. принадл-т мн-ву А, а вторая компонента принадл-т мн-ву В.
А={m; p}, B={e; f; k}
A×B={(m, e); (m, f); (m, k); (p, e); (p, f); (p, k)}
Св-ва умнож-я