2. Высказ-ия и высказыват-ые формы. Смысл логич-х связок «и», «или», «неверно, что» в составных высказ-ях. Высказ-ия с кванторами, способы установл-я их знач-я ист-ти.

Относ-но понятий и отнош-ий м-у ними м. высказывать различ. суждения. Языковой формой суждений явл-ся повествоват-е предложения (Число 12 – четное; 2+5>8; х+5=8). Они м.б. записаны как на естественном, так и на математич. языке.

Высказ-е – это предл-ие, в отнош-ии кот-го имеет смысл задать вопрос «истинно оно или ложно».

Определить истинность или ложность высказ-ия это значит найти знач-ие истинности высказ-ия.

Высказыват. форма – это предл-ие, содержащее одну или неск-ко переменных, кот. обращается высказ-ем при подстановке в него вместо переменных конкрет. знач-ий.

Высказывательная форма это есть предложение относительно которого не имеет смысл задавать вопрос об истинности или лжи.

По числу переменных, входящих в высказыват. форму, различают одноместные (х+5=8), двухместные (Прямая х параллельна прямой y) и т.д. Обознач-е: A(x), A(x,y) и т.д.

В высказыват. форме переменные м. содержаться неявно: «число четное» (подразум-ся: «число х – четное»)

Область опред-я высказыват. формы – знач-е переменных, при кот. высказыват. форма определена.

Мн-во истинности – знач-я переменных, кот. обращают высказыват. форму в истинное высказ-е (обознач.: Т).

Предл-я (высказ-я и высказыват. формы):

- простые, элементарные.

- сложные, составные (если тр-к равнобедр-й, то углы при основании в нем равны).

Составные предл-я образ-ся из простых при пом. логич. связок: «И», «Или», «Если то», «Не» и др.

Напр.: «число 28 четное и делится на 7».

Выявить логич. структуру математич-го предл-ия:

- опред-ть из каких эл-тов состоит предл-е

- с пом. каких логич. связок оно образовано.

Образ-е составного высказ-я с пом. логич. связки назыв-ся логической операцией.

Если высказ-е явл-ся простым математич. выраж-ем, то его знач-е ист-ти опред-ся на основе тех З., кот. имеются о рассматриваемом объекте.

Если высказ-е – составное математич. предл-е, то его знач-е ист-ти опред-ся по след-им правилам:

1) Смысл «и»

Конъюнкцией высказ-ий А и В наз-ся высказ-е A۸B, кот. истинно, когда обо высказ-я истины, и ложно, когда хотя бы одно высказ-е ложно.

А	В	A۸B
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

2) Смысл «или»

Дизъюнкцией высказ-ий А и В назыв. высказ-е AVB, кот. истинно, когда истинно хотя бы одно из этих высказ-ий, и ложно, когда оба высказ-ия ложны.

А	В	AVB
И	И	И
И	Л	И
Л	И	И
Л	Л	Л

3) Смысл «Неверно, что» (не)

Отрицанием высказ-я А наз-ся высказ-ие Ā, кот. ложно, когда высказ-е А истинно, и истинно, когда высказ-е А – ложно.

A	Ā
И	Л
Л	И

В формулировках математич. предл-ий часто встреч-ся слова: «каждый», «все», «некот-е», «хотя бы один».

Выражение «для всякого х» называется квантором общности.

(Vx) A(x) «для всякого значения х предложение А(х) – истинное высказывание». [V = перевернутая А]

Выражение «существует х такое, что…» называется квантором существования.

(Ех) А(х) «существует такое значение х, что А(х) – истинное высказывание». [Е = Е зеркальное]

«Всякий» = «все», «каждый», «любой».

«Существует» = «некоторые», «найдется хотя бы один», «есть хотя бы один».

Установл-е ист-ти для высказ-я с квантором общности:

Ист-ть высказ-я с квантором общности устанавл-ся путем док-ва.

Например:

Произвед-е любых 2ух последоват-х натур-х чисел кратно 2. Любой – V.

Выдвинем предпол-е, что высказ-е истинно. Чтобы обосновать ист-ть данного высказ-я, содержащего квантор общности, проведем док-во.

x₁=2n

x₂=2n+1

x₁*x₂=2n(2n+1), т.к. данное произвед-е содержит множ-ль, кратный 2, то всё произвед-е будет кратно 2.

Показать ложность таких высказ-ий м., приведя контрпример.

Например:

Произве-е любых 2х соседних натур-х чисел кратно 4.

3*2=6, 6:4 – доказана ложность данного высказ-я.

Установл-е ист-ти для высказ-я с квантором существования:

Ист-ть высказ-я с квантором существования устанавл-ся при пом. конкрет-го примера.

Например:

В некот-х тр-ках стороны равны (рисуем равнобедр-й тр-к и отмечаем равные стороны).

Чтобы убедиться в ложности такого высказ-я, нбх. привести док-во.

Например:

Хотя бы одно из чисел 0,1,2,3,4 явл-ся решением ур-ия -10x=20. Среди чисел 0,1,2,3,4 есть такое, кот-е явл-ся решением ур-ия.

Данное высказ-ие явл-ся ложным, оно содержит квантор существования. Чтобы доказать ложность данного высказывания, проведем док-во.

Док-во будем проводить методом полной индукции (рассмотрим все частные случаи).

х₁=0 => -10*0=20 – невер. числовое рав-во

х₂=1 => -10*1=20 – невер. числовое рав-во

х₃=2 => -10*2=20 – невер. числовое рав-во

х₄=3 => -10*3=20 – невер. числовое рав-во

х₅=4 => -10*4=20 – невер. числовое рав-во

3. Умозаключения (УЗ). Неполная индукция и аналогия. Примеры таких УЗ. Построения УЗ, с пом. кот. мл. шк-ки «открывают» св-во прямоуг-ка: «В любом прямоуг-ке диагонали равны». Пример использ-я в нач. курсе О. матем-ке УЗ по аналогии.

УЗ – это способ получ-я нов. З. на основе некоторого имеющегося. УЗ – это такая логич. операция, кот. позволяет из одного или нескольких предложений получить новое предложение, кот. будет содержать новые, по сравнению с исходными, знания.

УЗ состоит из посылок и заключения. Между посылками и заключ. сущ-ет опред. связь, благодаря которой мы получаем УЗ.

Посылки – это высказывания, содержащие исходное З.

Заключ-е – это высказ-ие, содержащее нов. З., полученное из исходного. В УЗ из посылок выводится заключ-е.

Рассм. примеры УЗ, кот. выполняют мл. шк-ки, изучая матем-ку.

Пример 1. Ученику предлаг-ся объяснить, почему число 23 м. представить в виде суммы 20 + 3. Он рассуждает:

«Число 23 – двузначное. Любое двузнач-е число м. представить в виде суммы разрядных слаг-ых. След-но, 23 = 20 + 3».

1ое и 2ое предл-ия в этом УЗ посылки, причем одна посылка общего хар-ра: высказ-е «любое двузнач. число м. представить в виде суммы разрядных слаг-ых», а др. – частная, она характериз. только число 23 – оно двузнач. Заключ-е – предл-е, кот. стоит после слова «след-но», - также носит частный хар-р, так как в нем речь идет о конкретном числе 23.

Пример 2. Один из приемов ознак-я мл. шк-ков с переместит-м св-вом умнож-я заключ-ся в следующем. Используя различ-е ср-ва наглядности, шк-ки вместе с (У) устанавл-ют, что 6•3=3•6, 5•2=2•5, 3•7=7•3. А затем, на основе получ-ых рав-в делают вывод: для всех натур-ых чисел а и b верно рав-во а•b=b•а.

УЗ бывают разные:

- дедуктивные (посылки и заключ-е находятся в отнош-и логич-го следования – пример 1)

- неполная индукция

- по аналогии

1) Дедуктивным назыв-ся УЗ, в кот. посылки и заключ-е находятся в отнош-ии логич-го следования.

2) Неполная индукция – УЗ, в кот. на основании того, что некот. объекты опред. класса обладают тем или иным св-вом, делается вывод о том, что этим св-вом обладают все эл-ты данного класса. Вид рассужд-я, кот. часто использ-ся в нач. шк. Такое рассужд-е м. привести как к истинным, так и к ложным выводам. Эти выводы д. носить хар-р гипотезы, кот. потом нужно доказать или опровергнуть. Неполная индукция не явл-ся доказательством.

Напр.: Для некот-х натур-ых чисел м. утверждать, что сумма < их произвед-я. На основании этого м. сделать вывод о том, что этим св-вом обладают все натур-ые числа, т.е. а+b<а*b. Но это утвержд-е ложно, в чем м. убедиться с помощью контрпримера: числа 1 и 2 – натуральные, но сумма 1+2>1*2.

3) Аналогия – УЗ, в кот. на основании сходства 2х объектов в некот-х признаках и при наличии дополнит-го признака у одного из них делается вывод о наличии такого же признака у др. объекта. Вывод по аналогии носит характер предпол-я, гипотезы, и поэтому д. б. доказан или опровергнут.

Термин «объект» использ-ся в широком смысле: им м. б. реальный предмет, модель, рис-к, числовое или буквенное выраж-е, задача и т.д. В кач-ве признаков м. выступать св-ва объектов, отнош-я м-у ними, способы ДД и т.д.

Напр.: (у) установил, что число делится на 6, если оно делится на 2 и на 3. Затем, действуя по аналогии, сделал вывод: число делится на 8, если оно делится на 2 и на 4. Чтобы убедиться в ложности получ-го вывода, достат-но привести контрпример: число 12 делится на 2 и на 4, но не делится на 8.

Аналогия м. б. использована для установления отнош-ий м-у данными объектами.

Напр., уч-ся установили, что 4•(3+7)>4•3+4•6, т. к. 4•(3+7)=4•3+4•7, а 4•7>4•6. Рассматривая затем выраж-я 3•(8+9) и 3•8+3•7, уч-ся м. по аналогии сделать вывод о том, что (8+9)>3•8+3•7. Проверить его прав-ть м. либо путем рассуждений, аналогичных тем, что проводились при выполнении 1го задания либо при пом. вычислений.

Примеры УЗ.

Неполная индукция:

3+3=6; 5+7=12; 1+1=2

Выделим некот. объекты из совокупности нат. чисел. 3,1,5,7 – рассмотрим их суммы. Их суммы – чётные числа. Предположим, что сумма двух нечётн. чисел есть число чётное.

Оно доказывается или опровергается.

3+2=5; 2+3=5

6+1=7; 1+6=7

5+4=9; 4+5=9

 от перемены мест слагаемых сумма не меняется.

По аналогии:

а) 45=40+5; 21=20+1; 34=10+4

 57=50+7

Построение УЗ, с пом. кот. мл. шк-ки «открывают» св-во прямоуг-ка: «В любом прямоуг-ке диагонали равны».

Уч-ся предлаг-ся на рассмотр-е неск-ко разных прямоуг-ков, у кот. требуется измерить диагонали. Уч-ся измеряют обе диагонали у кажд. прямоуг-ка, и на основе того, что они равны у всех прямоуг-ков, делают вывод: в люб. прямоуг-ке диагонали равны (неполная индукция).

Пример использ-я в нач. курсе О. матем-ке УЗ по аналогии.

После рассмотр-я способа умножения 27 на 3 (27•3=(20+7)•3=20•3+7•3=81) детям предлаг-ся умножить 712 на 4. Действуя по аналогии, они устанавл-т, что 712•4=(700+10+2) •4=2800+40+8=2848. Далее по аналогии устанавл-т, как умножить 6288 на 3.

4. Дедуктивные УЗ. Простейшие схемы дедукт-х УЗ. Примеры построения дедукт-х УЗ с использ-ем этих схем. Построение УЗ, доказыв-го, что: а) В заданном прямоуг-ке противоп-е стороны равны, б) Число 132 не кратно 5.

УЗ – способ получ-я нов. З. на основе некоторого имеющегося.

УЗ представляет собой логич-ю операцию, позволяющ. из одного или неск-их предл-ий получить нов., кот. содержит новые З. по отнош-ю к предыдущему предл-ию.

Каждое УЗ состоит из 2х посылок – общей и частной, и заключ-я. М-у посылками и заключ-ями сущ-ет опред-ая связь, благодаря кот. мы получаем УЗ.

Посылки – высказ-ия, содерж-ие исходное З.

Заключ-е – высказ-ие, содерж-ее новое З, полученное из исходного.

Например:

Общ. п.: «х:9  х:3»

Ч. п.: «27:9»

Закл.: « 27:3»

Дедуктивным наз-ся рассуждение (УЗ), в кот. посылки и заключ-е находятся в отнош-и логич-го следования.

В дедукт-м УЗ всегда из истинных посылок следует истинное заключ-е. Из истинных посылок НЕЛЬЗЯ получить ложное заключ-е.

Схемы дедуктивных рассуждений:

1) Правило заключения.

A(x)=>B(x), A(a)

B(a)

A(x)=>B(x) – общая посылка

A(a) – частная посылка

B(a) – заключение

2) Правило отрицания.

A(x)=>B(x), ¬B(a)

¬А(а)

3) Правило силлогизма.

A(x)=>B(x), B(x)=>C(x)

A(x)=>C(x)

Приведем пример умозаключения, выполненного по правилу заключения: Примеры построения дедукт-х УЗ с использ-ем этих схем.

1) Правило заключения

Если запись числа х оканч-ся цифрой 5, то число х делится на 5. Запись числа 135 оканч-ся цифрой 5. След-но, число 135 делится на 5.

2) Правило отрицания:

Если запись числа х оканч-ся цифрой 5, то число х делится на 5. Число 177 не делится на 5. След-но, оно не оканч-ся цифрой 5.

3) Правило силлогизма:

Если число х кратно 12, то оно кратно 6. Если число х кратно 6, то оно кратно 3. След-но, если число х кратно 12, то оно кратно 3.

Построение УЗ, доказыв-го, что:

а) в заданном прямоуг-ке противоп-ые стороны равны.

Если 4угольник явл-ся прямоуг-ком, то у него противопол-е стороны равны. 4угольник ABCD – прямоуг-к. Следоват-но, у него противопол-е стороны равны.

б) Число 132 не кратно 5 и др.

Если запись числа х оканч-ся цифрой 5, то число х кратно 5. Запись числа 132 не оканч-ся цифрой 5. Следоват-но, число 132 не кратно 5.

5. Понятие соответствия м-у мн-вами. Взаимно однозначные соответ-вия. Опред-ие числовой ф-ции. Способы задания ф-ций. Прямая и обратная пропорц-ти, их осн-е св-ва и графики. Примеры числовых ф-ций из нач. курса матем-ки, заданных при пом.: а) таблицы; б) выраж-я с перемен.; в) формулы.

Соответствием м-у эл-тами мн-ва X и эл-тами мн-ва Y назыв-ся всякое подмн-во декартова произвед-я мн-ва Х на мн-во Y.

Отнош-е есть частный случай понятия соответствие, в кот. в кач-ве мн-ва Y выступает само мн-во Х.

Соответствие принято обозначать буквами P, S, T, R и др. Если S – соответствие м-у эл-ми мн-в X и Y, то, согласно опред-ю, SСX×Y.

Х={-2;0;3;4}

Y={-1;2}

Т.к. соответствие – это подмн-во декартова произвед-я мн-в, то его м. задать при пом.:

1) перечисления эл-тов

2) характеристических св-в

3) графа

4) графика (если множества Х и Y – числовые)

Т: «x>y»

Т: {(0;-1); (3;-1); (3;2); (4;-1); (4;2)}

НА ГРАФИКЕ – ОТДЕЛЬНЫЕ ТОЧКИ

Мн-во назыв-ся упорядоченным, если на нем задано отнош-е порядка:

R – мн-во действит-х чисел

Т: «x<y» - отнош-е порядка

Отнош-е порядка обладает св-вами антисимметрич-ти и транзитив-ти, следоват-но, мн-во действит-х чисел явл-ся упорядоченным мн-вом.

1) X=R

Y={1; 2}

S: «x>y»

НА ГРАФИКЕ – ПРЯМЫЕ, ПАРАЛЛЕЛЬНЫЕ ОСИ Х (доходят до точек 1 и 2 соответств-но)

2) X={1; 2}

Y= R

S: «x<y»

НА ГРАФИКЕ – ПРЯМЫЕ, ПАРАЛЛЕЛЬНЫЕ ОСИ Y (доходят до точек 1 и 2 соответств-но)

Взаимно однознач-м соответств-м м-у эл-тами мн-ва Х и эл-тами мн-ва Y назыв-ся такое соответствие, когда кажд. эл-ту из мн-ва Х ставится в соответствие единств-ый эл-т из мн-ва Y и кажд. эл-т из мн-ва Y соответствует единственному эл-ту из мн-ва Х.

Х={1; 2; 3}

Y={a; b; c}

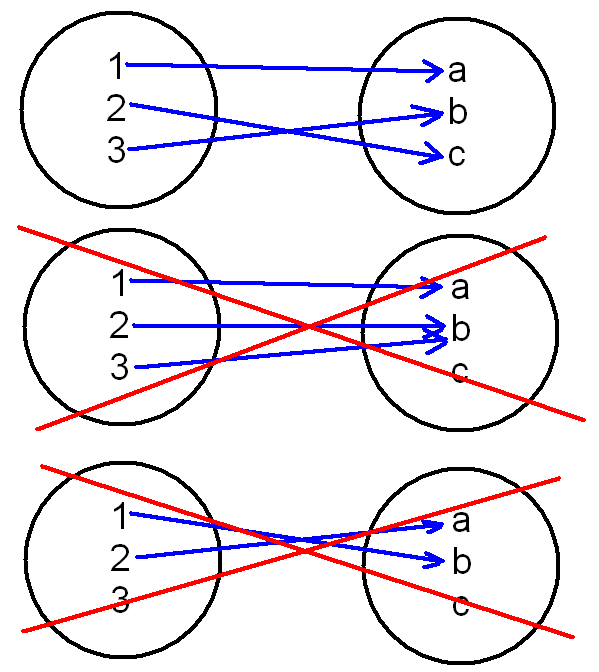
М-у мн-ми Х и Y существует взаимно однознач. соответствие, когда кажд-у действит-му числу соответствует единств-я точка координат. прямой и кажд. точка числовой прямой соответствует единств-му числу.

М-у мн-вом N и мн-вом точек числовой прямой м. установить взаимно однозначное соответствие.

Мн-ва X и Y называются равномощными, если м-у ними можно установить взаимно однозначное соответствие. X~Y

Пример: Пусть х – мн-во кружков, у – мн-во квадратов и соответствие м-у ними задано при пом. стрелок. Это соответствие взаимнооднозначно, т. к. кажд-у кружку из мн-ва х сопоставляется единств-й квадрат из мн-ва у и кажд. квадрат из у соответствует только 1му кружку из мн-ва х.

Отнош-е равномощности явл-ся отнош-ем эквивалентности, т.к. оно рефлексивно, симметрично и транзитивно.

Бесконеч-е мн-ва м. б. равномощными.

Если мн-ва конечны и равномощны, то они называются равночисл-ми. Если мн-ва конечны и содержат разное кол-во эл-тов, то они не м. б. равночисленными.

Если мн-во равномощно мн-ву натур-х чисел, то оно наз-ся счётным. Напр., мн-во чётных чисел; мн-во натур-х чисел; мн-во натур-х чисел, кратных 3.

Соответствие, обратное данному.

Пусть между эл-ми мн-ва Х и эл-ми мн-ва Y установлено соответствие Р, тогда Р^-1 называется обратным соответствием Р; если Y вступает в соответствие уР^-1х, то хРу.

X={a; b;c}

Y={2;3}

P={(a;2); (a;3); (b;2); (c;3)}

P^-1={(2;a); (3;a); (2;b); (3;c)}

Графики соответствий, кот. явл-ся обратными, симметрич. и симметрич. относит-но прямой y=x.

Числовой ф-цией наз-ся такое соответствие м-у числовым мн-вом Х и мн-вом R действит-х чисел, при кот. кажд-у числу из мн-ва X сопоставляется единств-ое число из мн-ва R.

Мн-во Х наз-ют областью опред-я ф-ции.

Ф-ции принято обознач. буквами f, g, h и др.

Мн-во чисел вида f(x) для всех х из мн-ва Х назыв-т областью знач-й ф-ции.

Ф-ция f назыв-ся монотонной на некот. промежутке А, если она на этом промежутке возрастает или убывает.

Ф-ция y=f(x) назыв-ся возраст-й на некот-м промежутке, кот. принадлежит области опред-ия этой ф-ции, если для любых x₁ и x₂ на этом промежутке вып-ся след-ее усл-е:

x₁>x₂ => f(x₁)<f(x₂)

Ф-ция y=f(x) назыв-ся убыв-й на некот-м промежутке, кот. принадлежит области опред-ия этой ф-ции, если для любых x₁ и x₂ на этом промежутке выполняется след-ее усл-е:

x₁<x₂ => f(x₁)>f(x₂)

Способы задания функций.

Для задания функции нбх. указать:

- числовое мн-во Х, т.е. область опред-я ф-ции;

- правило, по кот-му кажд-у числу из мн-ва Х соответствует единств-е дейст-ное число.

Способы задания:

1) С пом. формулы (y=2x-3, y=3x).

2) С пом. графика.

3) При пом. таблицы.

t (в часах)	0	3	6	9	12	15	18	21	24
p (в град.Цельсия)	-3	-7	-5	0	2	4	2	1	-3

Прямая и обрат. пропорц-ти, их осн-е св-ва и графики.

1) Прямой пропорц-тью назыв-ся ф-ция, кот. м. б. задана при пом. формулы y=kx, где k≠0 – действит-е число.

Св-ва прямопропорц-ой завис-ти:

- областью опред-я функции y=kx и областью ее знач-я явл-ся мн-во действит-х чисел R.

- графиком прямой пропорц-ти явл-ся прямая, проходящая через начало координат.

- при k>0 ф-ция возраст. на всей области опред-я; при k<0 – убывает.

- если ф-ция f – прямопропорц-ая завис-ть и (x₁, y₁), (x₂, y₂) – пары соответств-ых знач-ий переменных x и y, то с увелич-ем (уменьш-ем) знач-я переменной х в неск-ко раз соответств-е знач-е переменной у увелич-ся (уменьш-ся) во столько же раз.

2) Обратной пропорц-тью наз-ся ф-ция, кот. м. б. задана при пом. формулы y=k/x, где k≠0 – действит-ое число.

Св-ва обратнопропорц-ой завис-ти:

- область опред-я ф-ции и область знач-я – мн-во действит-х чисел, отличных от нуля.

- график – гипербола

- при k>0 ветви гиперболы распол-ны в 1й и 3й четвертях и ф-ция убывает на всей области опред-я х; при k<0 ветви гиперболы распол-ны во 2й и 4й четвертях и ф-ция возраст-т на всей области опред-я х.

- если ф-ция f – обратная пропорц-ть и (x₁, y₁), (x₂, y₂) – пары соответств-х знач-й переменных x и y, то (х₁/x₂)=(у₂/у₁). С увелич-ем (уменьш-ем) знач-я переменной х в неск-ко раз соответств-щее знач-е переменной у увелич-ся (уменьш-ся) во столько же раз.

Примеры числовых ф-ций из нач. курса матем-ки, заданных при пом.: а) таблицы; б) выраж-я с переем-ой; в) формулы.

6. Опред-ия отнош-ий на мн-ве. Способы задания отнош-ий. Отнош-ия эквивалент-ти и их связь с разбиением мн-ва на классы. Отнош-я порядка. Примеры заданий из учеб-ов мат-ки для нач. кл., при выполнении кот-х происходит: а) разбиение на классы с пом. отнош-я; б) упорядочение заданных мн-в.

Отнош-ем м-у эл-тами мн-ва Х или отнош-ем на множестве Х назыв-ся любое подмн-во декартова произвед-я мн-ва на себя. Отнош-е – это есть мн-во упорядоч-х пар.

Обознач-ся заглавными буквами лат. алфавита, причем принято брать буквы из конца алфавита.

Способы задания отнош-ий.

1) Перечисл-е входящих в него эл-тов (только конечное мн-во).

R={(2;1); (3;1); (3;2); (4;1); (4;3); (4;2)}

2) Характеристич-е св-во (в словесной форме, с пом. формулы).

R: «x>y»

3) Графич-й способ (представл-е данного отнош-я при помощи рисунков – графов)

Св-ва отнош-ий:

1) Св-во рефлексивности (около кажд. эл-та имеется стрелочка)

Отнош-е R, заданное на мн-ве Х, назыв-ся рефлексивным, если кажд. эл-т данного мн-ва вступает в отнош-е R с самим собой.

(R - рефлексивно) <=> (Vx€X xRx)

2) Св-во симметрич-ти (стрелочки в обе стороны)

Отнош-е R, заданное на мн-ве Х, назыв-ся симметрич., если из того, что эл-т х находится в отношении R с эл-том у, следует, что и эл-т у находится в отнош-и R c эл-том х.

(R - симметрично) <=> (xRy => yRx)

3) Св-во антисимметрич-ти (стрелочка только от одного эл-та к др-у, в обратную сторону стрелочки не д.б.).

Отнош-е R, заданное на мн-ве Х, обладает св-вом антисимметрич-ти, если для различ. эл-тов х и у из мн-ва Х из того, что эл-т х вступил в отнош-е R с эл-том у следует, что эл-т у в отнош-е R с эл-том х не вступает.

(R - антисимметрично) <=> (xRy и х≠y => ⌐yRx)

4) Св-во транзитив-ти (имеется тр-к)

Отнош-е R, заданное на мн-ве Х, назыв-ся транзитивным, если из того, что эл-т х находится в отнош-и R с эл-том у и эл-т у находится в отнош-ии R с эл-том z, следует, что эл-т x находится в отнош-и R с эл-том z.

(R - транзитивно) <=> (xRy и yRx => xRz)

Отнош-е R, заданное на мн-ве Х явл-ся отнош-ем эквивалент-ти, если оно обладает св-вами рефлексив-ти, симметрич-ти, транзитив-ти.

Q= {1/3; 2/3; 3/9; 2/6; 4/6; 1/12}

R: «x=y»

R={(1/3;1;3); (2/3;2/3); (3/9;3/9); (2/6;2/6); (4/6;4/6); (1/12;1/12); (1/3;3/9); (3/9;1/3); (1/3;2/6); (2/6;1/3); (2/6;3/9); (3/9;2/6); (2/3; 4/6); (4/6;2/3)}

Если на мн-ве Х задано отнош-е эквивалент-ти, то оно разбивает это мн-во на попарно непересекающ-ся подмн-ва (классы эквивалент-ти).

Напр.:

Х={1/2; 1/3; 1/4; 2/4; 2/6; 3/6}

Отнош-е рав-ва дробей. Мн-во разбилось на три подмн-ва: {1/2; 2/4; 3/6}, {1/3; 2/6}, {1/4}. Эти подмн-ва не пересек-ся, а их объед-е совпад. с мн-вом Х => мн-во Х разбито на классы.

Если на мн-ве задано отнош-е, кот. разбивает это мн-во на классы, то это отнош-е будет явл-ся отнош-ем эквивалент-ти.

Примеры: отнош-я рав-ва геометрич-х фигур, отнош-е параллельности прямых (при усл-и, что совпадающие прямые считаются параллельными)

Отнош-е R на мн-ве Х наз-ся отнош-ем порядка, если оно одновр-но обладает св-вами антисимметрич-ти и транзитив-ти.

Например:

Отнош-е «меньше» на мн-ве натур-х чисел.

X= {2; 7; 9; 11; 12}

S: «x>y»

S= {(7;2); (9;2); (9;7); (11;2); (11;7); (11;9); (12;2); (12;7); (12;9); (12;11)}

S – антисимметрич. и транзитив. => отнош-е S явл-ся отнош-ем порядка

Мн-во Х назыв-ся упорядоченным, если на нем задано отнош-е порядка.

Примеры заданий из учеб. матем-ки для нач. ., при вып-нии кот. происходит:

а) разбиение на классы с помощью отношения.

Какие из фигур на рис. имеют одинак. площадь? На рис. фигуры разбиты на клеточки; F1=9, F2=9, F3=6, F4=9, F5=12, F6=4, F7=6, F8=12. Отнош-е Х: «иметь одинак-ю площадь». Х={(F1; F2); (F1;F4); (F2; F1); (F2; F4); (F1; F1); (F2; F2); (F3; F7); (F3; F3); (F4; F1); (F4; F2); (F4;F4); (F5;F5); (F5; F8); (F6; F6); (F7; F7); (F7; F3); (F8; F8); (F8; F5)}

б) упорядочение заданных множеств.

На рис. даны 4 отрезка. Какие из этих отрезков длиннее др-х? a=4, b=2, c=6, d=8; X: «х длиннее у»; Х={(a;b); (d;a); (d;b); (d;c); (c;a); (c;b)}

7. Числовое выраж-е и выраж-е с переменной. Тождеств-е преобраз-я выраж-ий. Числовые рав-ва и нерав-ва, их осн-е св-ва. Примеры тождеств-х преобраз-ий выраж-й, выполняемых мл. шк-ками при изуч-и устных приемов умнож-я двузнач-х чисел на однознач-е.

Числовое выраж-е – это такое математич. предлож-е в записи кот. использ-ся числа, знаки действий скобок.

Напр.: 4+2; 3; 5•(8+3); 9•3+6:2

Читается числовое выраж-е по рез-ту послед. действия, выполн-го в этом выраж-ии.

Рез-т выполненных выраж-й действий назыв-ся его знач-ем.

Если знач-е выраж-я нельзя найти, то такое выраж-е назыв-ся выраж-ем, не имеющим смысла.

Напр.: (4:(3-3)).

Если в числ-м выраж-и число заменить буквой, то получ-ое математич. предл-ие будет называться выраж-ем с переменной.

Напр.: (4а-6; 3*a; 3*a + 6).

Те знач-я переменной, при кот. выраж-е имеет смысл наз-ся область опред-я выраж-я.

Если f и g – числовые выраж-я, то f±g; f•g; f:g – тоже будут явл-ся числовыми выраж-ями.

Два выраж-я назыв-ся тождественными, если при их любых знач-ях переменой из области опред-я этих выраж-й их соответств-ие знач-я равны.

Напр.: 5(х+2) =5х+10

Тождеств. преобраз-е выраж-я – переход от 1го выраж-я к выраж-ю, кот. явл-ся тождественно равным первому.

К тождеств. преобраз-ям выраж-й относятся:

- раскрытие скобок

- вынесение общего множ-ля за знак скобок

- привед-е подобных слаг-ых

- замена рез-та действий его знач-ем и т.д.

Числ-е рав-во.

Пусть f и g – два числ-х выраж-я. Соединим их знаком рав-ва. Получим предл-е f=g, кот. назыв-т числ-ым рав-вом.

Числ-е рав-ва бывают:

- истинные (3+2=6-1)

- ложные (3+2=7-3)

Числ-е рав-во истинно, если знач-я числовых выраж-й, стоящих в левой и правой частях рав-ва, совпадают.

Св-ва числ-х рав-в:

1) Если к обеим частям истинного числ-го рав-ва прибавить одно и то же числ-е выраж-е, имеющее смысл, то получим также истинное числ-е рав-во.

2) Если обе части истинного числ-го рав-ва умножить на одно и то же числ-е выраж-е, имеющее смысл, то получим также истинное числ-е рав-во.

Числ-е нерав-во.

Пусть f и g – два числ-х выраж-я. Соединим их знаком «>» (или «<»). Получим предл-ние f>g (или «f<g»), кот. назыв-т числ-ым нерав-вом.

Числ-е нерав-ва бывают:

- истинные (6+2>13-7)

- ложные (6+2<13-7)

Св-ва числ-ых нерав-в:

1) Если к обеим частям истинного числового нерав-ва прибавить одно и то же числ-е выраж-е, имеющее смысл, то получим также истинное числ-е нерав-во.

2) Если обе части истинного числ-го нерав-ва умножить на одно и то же числ-е выраж-е, имеющее смысл и положит-е знач-е, то получим также истинное числ-е нерав-во.

3) Если обе части истинного числ-го нерав-ва умножим на одно и то же числ-е выраж-е, имеющее смысл и отриц-е знач-е, а также поменяем знак нерав-ва на противопол-й, то получим также истинное числ-е нерав-во.

Примеры тождест-х преобраз-й выраж-й, выполняемых мл. шк-ками при изуч-и устных приемов умнож-я двузнач-х чисел на однознач-е.