Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донбасский государственный педагогический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Мет_Практ №1 (n-мерные векторы и их системы).doc

Скачиваний:

Добавлен:

31.08.2019

Размер:

542.21 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

3. Краткие теоретические сведения

В геометрии вектором называется направленный отрезок. В фиксированной системе координат каждый вектор a однозначно определяется своими координатами:

, (1)

где называются координатами вектора a.

Если какой-либо другой вектор, то

, (2)

, (3)

где k – число.

Сложение векторов и умножение вектора на число называется линейными операциями над векторами.

Обобщим понятие вектора следующим образом: назовем последовательность n чисел n-мерным вектором и представим его в виде (1). Число a₁ называется первой координатой вектора a; a₂ – второй координатой и т.д., а число n (количество координат) называется размерностью вектора а.

Два n-мерных вектора:

считаются равными только тогда, когда равны их соответствующие координаты

, ,…, .

Очевидно, что для любого вектора а: , где . Вектор O называется нулевым.

Вектор (-1)a называется противоположным вектору a и обозначается -a, т.е. . Ясно, что , вместо .

Так как операции над n-мерными векторами определяются через операции над их координатами, свойства арифметических операций справедливы и для операций над векторами.

(сложение коммутативно);
(сложение ассоциативно);
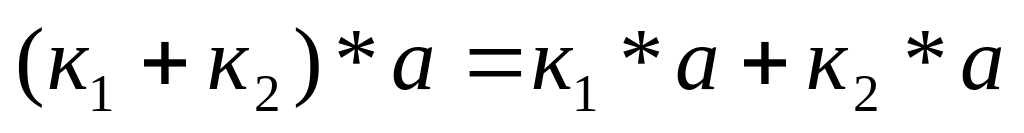(сложение дистрибутивно);
(сложение дистрибутивно);
,

где – некоторые вещественные числа.

Скалярное произведение и длина n-мерных векторов

Как известно из геометрии, если векторы а и b заданы своими координатами и , то их скалярное произведение ab определяется по формуле:

По аналогии скалярным произведением n-мерных векторов и называется число .

Некоторые свойства произведения чисел справедливы и для скалярного произведения векторов:

, где k – число.
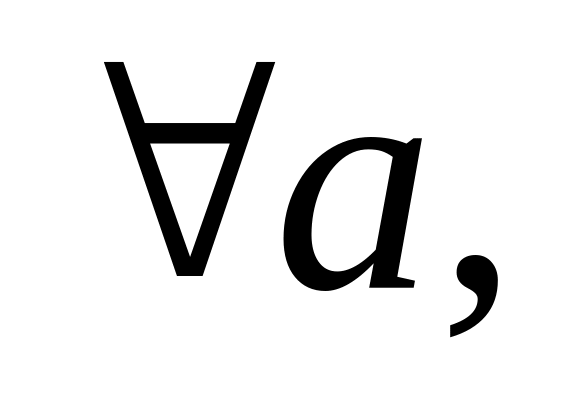причем тогда и только тогда, когда (нулевой вектор).

Длиной n-мерного вектора a называется число . Длина вектора a обозначается .

Из 4 свойства скалярного произведения векторов вытекает, что каждый n-мерный вектор a обладает длиной, причем нулевой вектор O, является единственным вектором, длина которого равна нулю.

Если а и b – n-мерные векторы, то справедливы следующие числовые соотношения:

, k – число;
(неравенство Коши-Буняковского);
(неравенство треугольника).

Вектор называется нормированным, если его длина равна 1.

Каждый вектор a можно нормировать, т.е. умножить на число k, чтобы вектор ka был нормированным.

, .

Угол между n-мерными векторами

Из неравенства Коши-Буняковского следует:

Углом между n-мерными векторами a и b называется значение; которое получается из решения уравнения (4):

, которое принадлежит отрезку .

Причем решение единственно при любых и . Следовательно, и угол между векторами a и b определен однозначно.

Перепишем соотношение (4) в виде

отсюда следует, что скалярное произведение векторов a и b равно произведению длин этих векторов на косинус угла между ними.

Геометрическая характеристика векторов – длина вектора и угол между векторами, – позволяют сформулировать критерий равенства n-мерных векторов.

Теорема: ненулевые n-мерные вектора а и b равны тогда и только тогда, когда угол между ними равен нулю и длины этих векторов равны.

Коллинеарные вектора

Два ненулевых n-мерных вектора называются коллинеарными, если угол между ними равен 0 или .

Если , то коллинеарные вектора считаются одинаково направленными, если же , то коллинеарные вектора противоположно направлены. Символичная запись означает, что векторы а и b одинаково (противоположно) направлены.

Ненулевые векторы a и b называются неколлинеарными, если угол между ними >0 и <.

Ненулевые векторы а и b коллинеарны тогда и только тогда, когда можно подобрать такое k (число), что .

Разложение вектора по системе векторов

Пусть дана система n -мерных векторов выбираем n – произвольных чисел . Заметим, что чисел ровно столько, сколько векторов в системе.

Вектор называется линейной комбинацией векторов с коэффициентами .

Пусть теперь наряду с векторами дан еще -мерный вектор . Будем говорить, что вектор линейно выражается через векторы , если он равен некоторой линейной комбинации векторов, т.е. найдется такой набор чисел , что

. (5)

В этом случае будем говорить также, что вектор разлагается по векторам . Числа называются коэффициентами разложения вектора по системе .

Разложение считается отличным от разложения (5), если различна хотя бы одна пара соответствующих коэффициентов разложения (т.е. хотя бы один ).

Справедливы следующие утверждения:

Нулевой вектор разлагается по каждой системе векторов

Если вектор разлагается по части системы векторов , то он разлагается и по всей системе векторов.

Предположим, что часть системы векторов можно представить

, где

тогда

Каждый - мерный вектор разлагается по диагональной системе - мерных векторов:

с коэффициентами, которые равны координатам вектора .

В самом деле

Если вектор разлагается по системе векторов , а каждый вектор этой системы разлагается по системе векторов , то вектор разлагается по системе векторов .

Из условия следует, что

После подстановки получаем:

Т.е. вектор разлагается по векторам .

Векторная формула системы линейных уравнений

Используя введенные операции над векторами, запишем систему линейных уравнений:

в векторной форме.

Обозначим столбцы коэффициентов при неизвестных

, , ; .

Тогда систему (1) можно представить в виде:

(2)

Уравнение (2) называется векторной формой системы линейных уравнений (1). Последовательность чисел называют решением системы (2), если - верное векторное равенство.

Пусть n-мерный вектор ( ) является решением системы (3). Тогда ясно, что для разложения вектора по системе достаточно найти решение системы линейных уравнений (2).

Пример: дана система векторов и вектор

; ; ; ; .

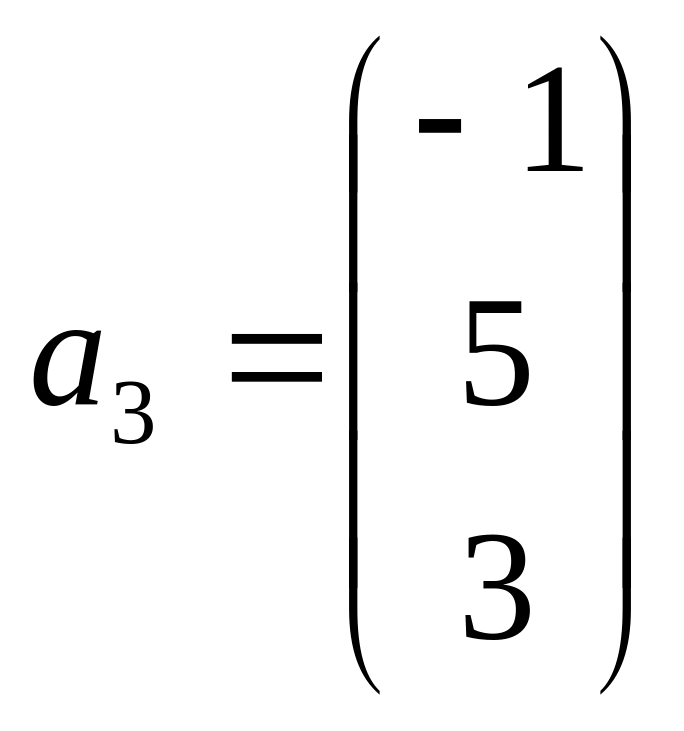Выяснить разлагается ли вектор по системе векторов .

Для этого необходимо решить систему уравнений

И меем:

Общее решение системы имеет вид:

Главные неизвестные и , так как получена система 2 уравнений (остальные линейно зависимы).

Общее решение:

Достаточно положить свободные неизвестные и произвольные значения и получить разложение вектора по системе векторов .

Например:

, тогда , .

Следовательно:

Если же , тогда

и .

Линейная зависимость и линейная независимость системы векторов.

Система векторов а₁, а₂, …, а_n называется линейно зависимой, если система уравнений

a₁x₁ + a₂x₂ + … + а_nx_n = 0 (1)

имеет ненулевое решение, если же система уравнений не имеет ненулевых решений, то система векторов a₁, a₂ …, a_n называется линейно независимой.

Будем говорить, что набор чисел k₁, k₂, … k_n является ненулевым, если хотя бы одно из чисел k отлично от нуля.

Для линейно зависимых систем векторов (линейно независимых) справедливы следующие утверждения:

Система векторов, состоящая из одного вектора a ≠ 0 линейно независима.

В самом деле, из любого соотношения a = 0 и a ≠ 0 → k = 0, что и означает линейную независимость системы.

Диагональная система векторов

; ; …, ;

линейно независима.

Запишем систему уравнений

e₁x₁+e₂x₂+…e_nx_n = 0 (2)

в виде таблицы

x₁	x₂	…	x_n
1	0	…	0	0
0	1	…	0	0
0	0	…	1	0

Откуда ясно, что система уравнений (2) имеет единственное решение x₁=0; x₂=0…x_n=0, т. е. не имеет не нулевых решений и поэтому диагональная система векторов линейно независима.

Система векторов a₁, a₂ …, a_n линейно зависима, если хотя бы один из векторов системы разлагается по остальным векторам этой системы.

Пусть какой-нибудь вектор А1 разлагается по остальным векторам системы

a₁=l₂a₂+l₃a₃+…+l_na_n(3)

Представим (3) в виде

-1a₁+l₂a₂+l₃a₃…+l_na_n=0

Так как набор чисел (решение) -1, l₂, l₃…, l_n – не нулевой, система векторов a₁, a₂,…,a_n –линейно зависима.

Система m мерных векторов a₁, a₂,…, a_n линейно зависима, если n<m.

Действительно система уравнений

a₁x₁+a₂x₂+…+a_nx_n=0 (4)

содержит m уравнений и n неизвестных.

Так как по условию n>m, то из теории «Система однородных уравнений, в которой число уравнений меньше числа неизвестных, всегда имеет нулевое решение» вытекает, что система уравнений (4) обладает ненулевым решением. Следовательно, система векторов a_1,a_2,_…,a_nлинейно зависима.

Свойства линейно зависимых и линейно независимых систем векторов

1. Непосредственно из определений видно, что каждая система векторов либо линейно зависима, либо линейно независима.

2. Если часть системы векторов a₁, a₂, …, a_n линейно зависима, то и вся система линейно зависима.

Допустим, что часть, состоящая из векторов a₁, a₂,…, a_p линейно зависима, т. е. k₁a₁+k₂a₂+…k_pa_p=0 и k₁k₂…, k_p ненулевой набор чисел. Тогда соотношение

k₁a₁+k₂a₂+…+ k_pa_p+ a_p+1+ a_p+2+…+ a_n=0

выполняется с не нулевым набором чисел.k₁, k₂…k_p, 0, 0 - что и означает линейную зависимость системы a₁,…,a_n.

3.Если система векторов a₁, …, a_n линейно независима, то и любая ее часть линейно независима.

Докажем это свойство от противного.

Предположим, что часть системы линейно зависима. Тогда из свойства (2) следует, что и вся система линейно зависима, однако это противоречит условию. Следовательно, любая часть данной системы линейно не зависима.

4. Если система векторов a₁, a₂,…, a_n линейно зависима, то хотя бы один из векторов этой системы разлагается по остальным ее векторам.

5. Если система векторов a₁, a₂,…, a_n линейно зависима, а ее часть линейно не зависима a₁…, a_n_-1, то вектор a_n разлагается по векторам a₁, a₂,…, a_n_-1.

Пример 1

Выяснить, является ли данная система векторов линейно зависимой или линейно независимой.

a₁=(3, 5, 1, 4), a₂=(-2, 1,-5, -7), a₃= (-1, -2, 0, -1)

Преобразуем систему линейных уравнений

a₁x₁+a₂x₂+a₃x₃=0 методом Гаусса, (столбец свободных членов состоит только из нулей и не изменяется в процессе преобразований, поэтому его можно не записывать)