Термодинамика линейных необратимых систем
1. Соотношения взаимности Онзагера
2. Принцип Кюри
3. Явление термодиффузии и диффузионный термоэффект
4. Стационарные неравновесные состояния
5. Устойчивость стационарных состояний
6. Теорема Пригожина о минимуме производства энтропии
6.1. Доказательство необходимого условия
6.2. Доказательство достаточного условия
7. Определение диаметра включения, устойчивого к дроблению
7.1. Постановка задачи
7.2. Исследование экстремума производства энтропии системы
7.3. Устойчивость стационарного состояния
8. Определение порозности слоя …
1. Соотношения взаимности Онзагера
В термодинамике необратимых процессов Ларс Онзагер сформулировал следующее положение: при небольших отклонениях от равновесия термодинамический поток можно представить в виде линейной комбинации термодинамических движущих сил:
(4.1)
Здесь
– движущая сила, сопряжённая с потоком
;
она определяет прямой эффект.
– движущие силы, сопряжённые с другими
потоками; они характеризуют в (4.1)
перекрёстные эффекты по отношению
к процессу i. Коэффициенты
L называют
феноменологическими коэффициентами:
– при прямом эффекте,
– при перекрёстных эффектах, причём
влияние прямого эффекта существенно
превышает влияние перекрёстных эффектов:
Соотношения типа (4.1) для систем, близких к равновесию, называют соотношениями взаимности Онзагера или линейными соотношениями.
С учётом (4.1) производство энтропии системы можно представить в виде квадратичной формы:
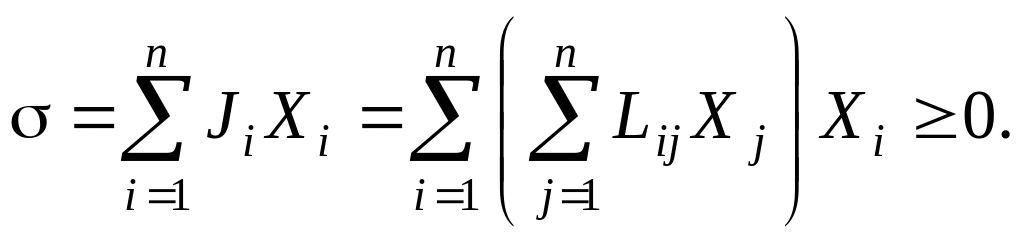
Данная квадратичная форма является положительно определённой (доказательство приводится в разделе "Характеристика производства энтропии").
Л. Онзагер также определил, что в линейных соотношениях (4.1) недиагональные коэффициенты равны [9]:
(4.2)
т.е. матрица
феноменологических коэффициентов
должна быть симметричной. Иными словами,
если на поток
,
соответствующий необратимому процессу
i, действует сила
необратимого процесса j, то сила
действует на поток
с тем же коэффициентом
.
Соотношения (4.2) называют принципом
симметрии феноменологических
коэффициентов.
2. Принцип Кюри
В термодинамике существует принцип Кюри для изотропных систем, свойства которых одинаковы во всех направлениях: потоки и движущие силы разной тензорной размерности не могут быть связаны друг с другом. Так например, причина-скаляр не может вызвать векторный поток.
Таким образом, согласно принципу Кюри линейные соотношения (4.1) и принцип симметрии феноменологических коэффициентов (4.2) справедливы только для потоков и сил одинаковой тензорной размерности.
По тензорной размерности необратимые процессы можно разделить на три группы:
1. скалярные – химические реакции, теплообмен и массообмен между фазами;
2. векторные – диффузия и теплопроводность в сплошной фазе, вязкое взаимодействие между фазами;
3. тензорные – вязкое взаимодействие в сплошной фазе.
Движущей
силой химических реакций является
химическое сродство, а потоком –скорость
реакции. Например, для реакции
:
где w – скорость реакции; k – константа скорости реакции; А – химическое сродство реакции; Kp – константа равновесия реакции; x, y, c – концентрации компонентов X, Y, C; Т – температура реакции; R – универсальная газовая постоянная.
Подробное описание потоков и движущих сил остальных необратимых процессов приведено в разделе "Структура производства энтропии".
В рамках термодинамики необратимых процессов определить конкретные границы применимости линейных соотношений невозможно. Эксперимент показывает, что для процессов диффузии и теплопроводности линейные соотношения справедливы в достаточно широкой области параметров. Для химических реакций линейные соотношения w = LA оказываются справедливыми только в очень узкой области, вблизи состояния химического равновесия. Тем не менее, если для описания состояния системы (независимо от того, какие процессы в ней протекают) применимы линейные соотношения (4.1), то это состояние условно характеризуют, как близкое к равновесию, а систему называют линейной.