Системы двух случайных величин

Двумерной называют СВ (Х,У), возможные значения которой есть пары чисел (х, у). Составляющие Х и У, рассматриваемые одновременно, образуют систему двух случайных величин.

Дискретной называют двумерную величину, составляющие которой дискретны. Если составляющие непрерывны, двумерная величина называется непрерывной.

Законом распределения вероятностей двумерной СВ называют соответствие между возможными значениями и их вероятностями ( ).

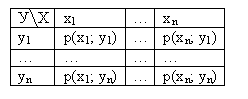
Зная закон распределения ДДвСВ можно найти законы каждой из сотавляющих: чтобы найти вероятность Р(Х=хi) надо просуммировать вероятности столбца хi, сложив вероятности строки уi, получим вероятность Р(У=уi).

Функцией распределения вероятностей ДвСВ называют функцию F(x, y), определяющую для каждой пары чисел (х, у) вероятность того, что Х примет значение меньше х, при этом У примет значение меньшее у:

F(x, y)=P(X<x, Y<y)

Вероятность попадания случайной точки в прямоугольник

Плотностью совместного распределения вероятностей НДвСВ называется смешанная производная второго порядка функции распределения

Тогда

Вероятность попадания случайной точки в область D

ДДвСВ: Условным распределением составляющей Х при У=уj называют совокупность условных вероятностей

где

Аналогично, условное распределение У при Х=хi –

где .

НДвСВ: Условной плотностью φ(Х|У) распределения составляющих Х при значении У=у назвается отношение плотности совместного распределения f(х, у) системы (Х,У) к плотности распределения f₂(у) составляющей У:

Функция φ(Х|У) дает распределение Х при условии, что У приняла значение у; f₁(x) дает распределение Х независимо от того, какие значения из возможных приняла У.

Аналогично, условная плотность У распределения при Х=х

Числовые характеристики системы двух случайных величин

1. Математическое ожидание и дисперсия

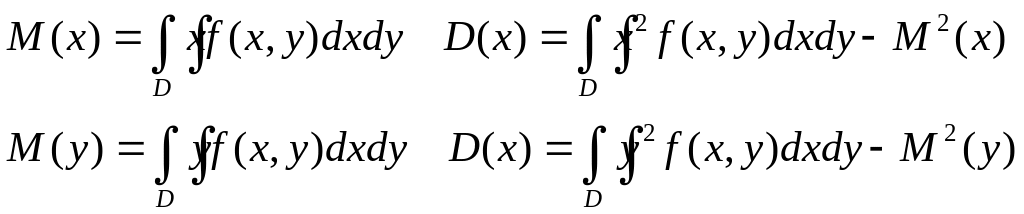
Условным математическим ожиданием НСВ У при Х=х называется

Условное математическое ожидание НСВ У при Х=х есть функция регрессии У на Х

Аналогично,

Условное математическое ожидание НСВ Х при У=у есть функция регрессии Х на У

Для ДСВ и

2. Корреляционный момент и коэффициент корреляции

Корреляционным моментом μ_ху СВ Х и У называется математическое ожидание произведение отклонений этих величин:

Корреляционный момент служит для характеристики связи между Х и У

Если Х и У независимы, то μ_ху=0

Коэффициентом корреляции r_ху СВ Х и У называется отношение корреляционного момента к произведению средних квадратических отклонений этих величин

,

Коэффициент корреляции служит для оценки тесноты линейной связи Х и У: чем ближе модуль коэффициента корреляции к 1, тем связь сильнее, чем ближе к 0, тем связь слабее.

Коррелированными называются две СВ, если μ_ху≠0. Если μ_ху=0, то Х и У некоррелированные.

Выборочное уравнение регрессии

Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой.

Корреляционной называют статистическую зависимость, проявляющуюся в том, что при изменении одной из величин изменяется среднее значение другой.

Условным средним называется среднее арифметическое наблюдавшихся значений У, соответствующих Х=х.

Условным средним называется среднее арифметическое наблюдавшихся значений Х, соответствующих У=у.

Условные средние являются оценками условных математических ожиданий:

Выборочное уравнение регрессии У на Х –

- выборочной регрессией У на Х, ее график – выборочной линией регрессии У на Х.

Аналогично, уравнение выборочным уравнением регрессии Х на У, - выборочной регрессией Х на У, ее график – выборочной линией регрессии Х на У

Обычно уравнение регрессии У на Х ищут в виде прямой линии

Угловой коэффициент прямой линии регрессии У на Х называется выборочным коэффициентом регрессии У на Х и обозначают ρ_ух

Для отыскания коэффициентов ρ_ух и b пользуются методом наименьших квадратов.

В качестве критерия рассмотрим функцию F(ρ, b) и найдем ее минимум.

Получим систему линейных уравнений

Решив систему найдем искомые коэффициенты

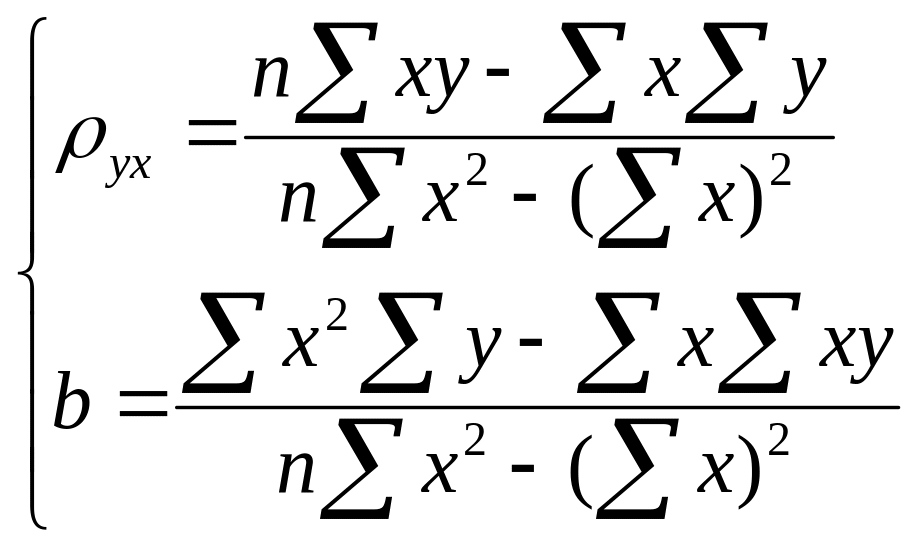
Аналогично находят выборочное уравнение прямой линии регрессии Х на У –

Уравнение прямой линии регрессии (по сгруппированным данным)

При большом числе наблюдений одно и то же значение х может встретиться n_х раз, одно и то же значение у – n_у раз, одна и та же пара чисел (х, у) – n_ху раз. Данные наблюдений группируют в корреляционную таблицу:

n_ху – в прямоугольнике на пересечении значений х и у;

n_у – сумма частот строк (у);

n_x – сумма частот столбцов (х);

n – сумма всех частот

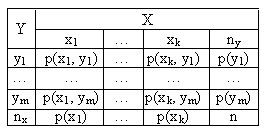
Тогда система для отыскания коэффициентов прямой линии регрессии У на Х примет вид:

Решив систему, найдем коэффициенты ρ_ух и b, а также само уравнение.

Однако, удобнее переписать уравнение в виде

где , , ,

r_в называется выборочным коэффициентом корреляции и является оценкой коэффициента корреляции.

Аналогично, , где

Если данные наблюдений над признаками Х и У заданы в виде корреляционной таблицы с равноотстоящими вариантами, то целесообразно перейти к условным вариантам:

где С₁ – ложный нуль варианты Х (варианта с наибольшей частотой); С₂ – ложный нуль варианты У; h₁ – шаг варианты Х (разность между двумя соседними вариантами), h₂ – шаг варианты У.

Выборочный коэффициент корреляции

где

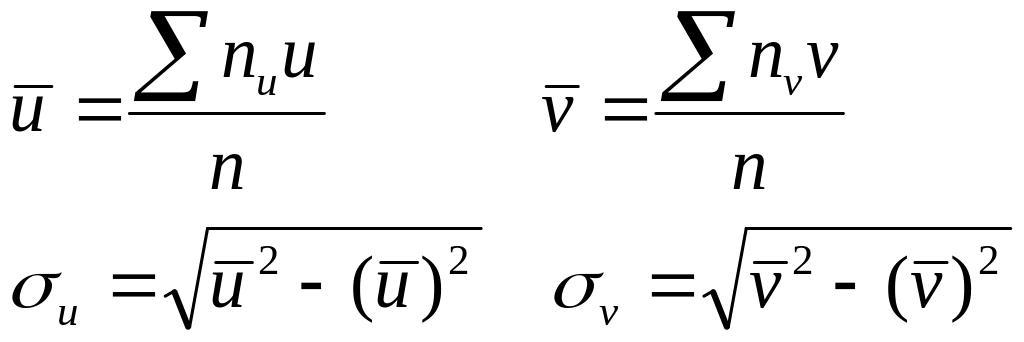
Определяют величины

Подставляют их в уравнения регресии и