
- •17. Случайные величины.
- •17.1. Закон распределения дискретной случайной величины.
- •17.2. Математическое ожидание дискретной случайной величины.
- •17.3. Дисперсия дискретной случайной величины.
- •17.5. Непрерывные случайные величины.
- •Функция распределения непрерывной случайной величины.
- •Плотность вероятности.
- •17.6. Мода и медиана. Квантили. Моменты случайных величин.
- •18. Основные законы распределения.
- •18.1. Биноминальный закон распределения.
- •18.2. Закон распределения Пуассона.
- •18.3. Геометрическое распределение.
- •18.4. Гипергеометрическое распределение.
- •1 8.5. Равномерный закон распределения.
- •18.6. Показательный (экспоненциальный) закон распределения.
- •18.7. Нормальный закон распределения.
18.6. Показательный (экспоненциальный) закон распределения.
Н епрерывная
случайная величина Х
имеет показательный (экспоненциальный)
закон распределения с параметром
,
если ее плотность вероятности имеет
вид:
епрерывная
случайная величина Х
имеет показательный (экспоненциальный)
закон распределения с параметром
,
если ее плотность вероятности имеет
вид:
![]()
Функция распределения случайной величины Х, распределенной по показательному (экспоненциальному) закону, есть
![]()
математическое
ожидание
![]() ,
,
![]() .
.
Показательный закон распределения играет большую роль в теории массового обслуживания и теории надежности.
18.7. Нормальный закон распределения.
Непрерывная
случайная величина Х
имеет нормальный закон распределения
(закон Гаусса) с параметрами а
и
![]() ,
если ее плотность вероятности имеет
вид
,
если ее плотность вероятности имеет
вид
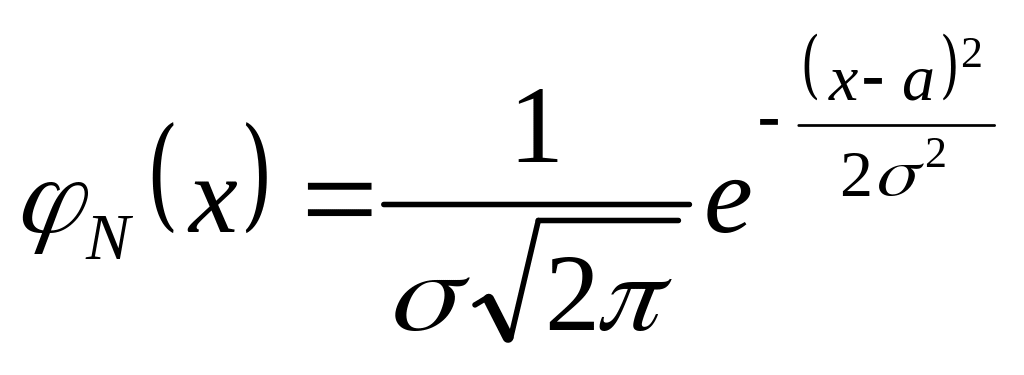 .
.
Н ормальный
закон распределения является предельным
законом, к которому приближаются другие
законы распределения при некоторых
типичных условиях. Этот закон наиболее
часто встречается на практике. Кривая
нормального распределения называется
нормальной или гауссовой кривой.
ормальный
закон распределения является предельным
законом, к которому приближаются другие
законы распределения при некоторых
типичных условиях. Этот закон наиболее
часто встречается на практике. Кривая
нормального распределения называется
нормальной или гауссовой кривой.
Математическое
ожидание случайной величины Х,
распределенной по нормальному закону,
равно параметру а
этого закона, т.е.
![]() ,
а ее дисперсия – параметру
,
а ее дисперсия – параметру
![]() ,
т.е.
,
т.е.
![]() .
.
Функция
распределения случайной величины Х,
распределенной по нормальному закону,
выражается через функцию Лапласа Ф(Х)
по формуле
![]() .
.
Случайная величина, распределенная по нормальному закону, обладает следующими свойствами:
Вероятность попадания случайной величины Х в интервал
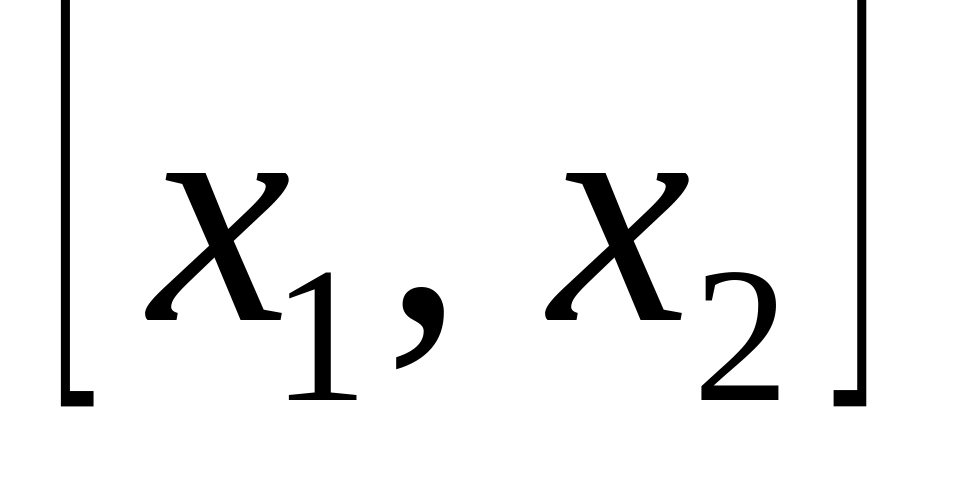 равна
равна
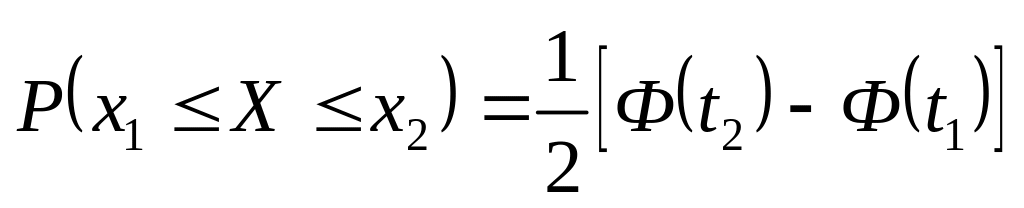 ,
где
,
где
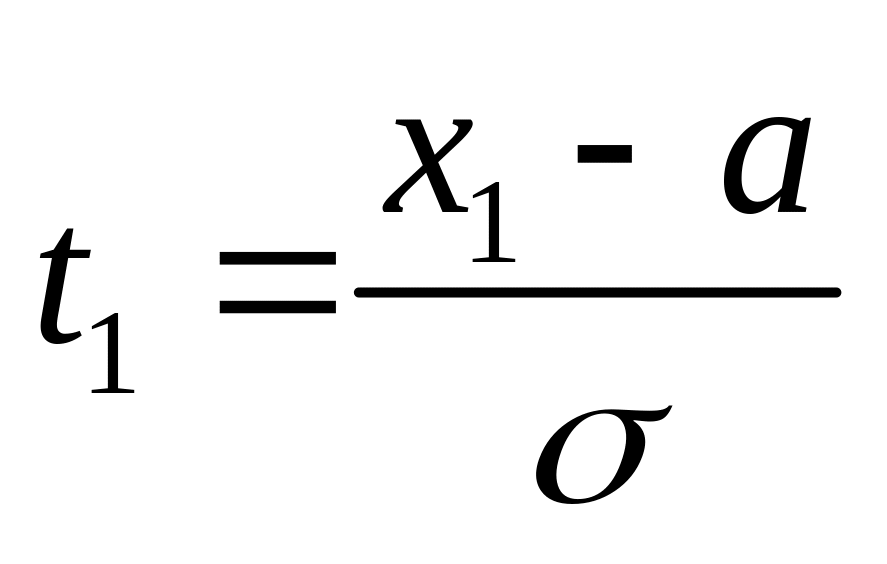 ,
,
 .
.Вероятность того, что отклонение случайной величины Х от математического ожидания не превысит величину
 (по абсолютной величине), равна
(по абсолютной величине), равна
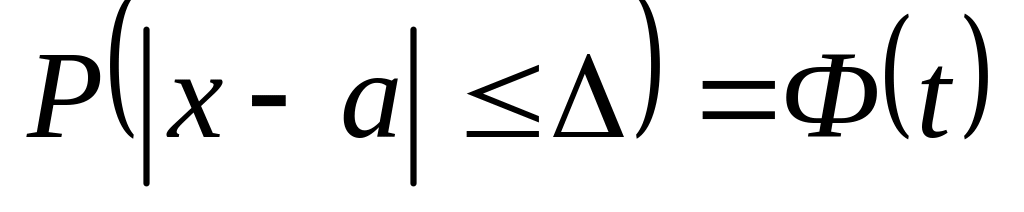 ,
где
,
где
 .
.
Правило трех сигм.
Если
случайная величина Х
имеет нормальный закон распределения
с параметрами а
и
,
то практически достоверно, что ее
значения заключены в интервале
![]() .
.
Пример.
Полагая, что рост мужчины определенной
возрастной группы есть нормально
распределенная случайная величина Х
с параметрами
![]() ,
найти:
,
найти:
1.
а) выражение плотности вероятности и
функции распределения случайной величины
Х;
б) доли костюмов 4-го роста (176 – 182 см) и
3-го роста (170 – 176 см), которые нужно
предусмотреть в общем объеме производства
для данной возрастной группы; в) квантиль
![]() и 10% точку случайной величины Х.
и 10% точку случайной величины Х.
2. Сформулировать «правило трех сигм» для случайной величины Х.
1.
а)
![]()
![]()
б) Доля костюмов 4-го роста (176 – 182 см) в общем объеме производства определяется по формуле как вероятность
![]()
![]()
![]()
![]()
Долю
костюмов 3-го роста (170 – 176 см) можно
высчитать проще, учитывая, что данный
интервал симметричен относительно
математического ожидания
![]()
![]()
в) Квантиль случайной величины Х найдем из уравнения с учетом
![]()
![]()
Это
означает, что 70% мужчин данной возрастной
группы имеют рост до 176 см. 10% точка –
это квантиль
![]() ,
т.е. 10% мужчин имеют рост не менее 181 см.
,
т.е. 10% мужчин имеют рост не менее 181 см.
2.
Практически достоверно, что рост мужчин
данной возрастной группы заключен в
границах
![]()
![]()
19. Закон больших чисел.
Под законом больших чисел в широком смысле понимается общий принцип, согласно которому совокупное действие большого числа случайных факторов приводит (при некоторых весьма общих условиях) к результату, почти независящему от случая. Т.е. при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности. (А.Н. Колмогоров)
19.1. Неравенство Маркова (лемма Чебышева).
Если
случайная величина Х
принимает только неотрицательные
значения и имеет математическое ожидание,
то для любого положительного числа А
верно неравенство
![]() .
.
19.2. Неравенство Чебышева.
Для любой случайной величины, имеющей математическое ожидание и дисперсию, справедливо неравенство
![]() .
.
![]() .
.
Первое неравенство устанавливает верхнюю границу вероятности рассматриваемого события, а вторая – нижнюю границу.
19.3. Теорема Чебышева.
Если
дисперсии п
независимых случайных величин
![]() ограничены одной и той же постоянной,
то при неограниченном увеличении числа
п
средняя арифметическая случайных
величин сходится по вероятности к
средней арифметической их математических
ожиданий
ограничены одной и той же постоянной,
то при неограниченном увеличении числа
п
средняя арифметическая случайных
величин сходится по вероятности к
средней арифметической их математических
ожиданий
![]() ,
т.е.
,
т.е.
![]() .
.
Если независимые случайные величины имеют одинаковые математические ожидания, равные а, а их дисперсии ограничены одной и той же постоянной, то неравенство Чебышева примет вид
![]() .
.
