17. Случайные величины.

17.1. Закон распределения дискретной случайной величины.

Будем полагать, что результатом реального опыта (эксперимента) может быть один или несколько взаимоисключающих исходов; эти исходы неразложимы и взаимно исключают друг друга. В этом случае говорят, что эксперимент заканчивается одним и только одним элементарным исходом.

Множество всех элементарных событий, имеющих место в результате случайного эксперимента, называется пространством элементарных событий (элементарное событие соответствует элементарному исходу).

Случайными событиями (событиями), будем называть подмножества пространства элементарных событий .

Случайной величиной Х называется функция, заданная на множестве элементарных исходов (или в пространстве элементарных событий): ,

Пример 1. Подбросим монету один раз. Монета может упасть цифрой вверх - элементарное событие , или гербом - элементарное событие . Соответствующее пространство элементарных событий состоит из двух элементарных событий:

Пример 2. Бросаем один раз игральную кость. В этом опыте пространство элементарных событий , где - выпадение i очков. Событие A - выпадение нечетного числа очков, .

Пример 3. На отрезке [0, 1] наугад (случайно) поставлена точка. Измеряется расстояние точки от левого конца отрезка. В этом опыте пространство элементарных событий - множество действительных чисел на единичном отрезке.

В более точных, формальных терминах элементарные события и пространство элементарных событий описывают следующим образом.

Случайной величиной называется величина, которая в результате опыта может принять определенное (но заранее неизвестное) значение.

Дискретной называют случайную величину, возможные значения которой есть отдельные изолированные числа (их можно пронумеровать).

Непрерывной называется случайная величина, которая может принимать любое значение из некоторого конечного или бесконечного промежутка.

Для дискретной случайной величины множество возможных значений случайной величины конечно или счетно, для непрерывной – бесконечно и несчетно.

Каждое значение дискретной случайной величины появляется с некоторой вероятностью.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически.

Простейшей формой задания закона распределения дискретной случайной величины Х является таблица (матрица), которая называется рядом распределения дискретной случайной величины.

		…		…
		…		…

или .

Ряд распределения может быть изображен графически в виде ломанной, которая называется многоугольником или полигоном распределения вероятностей.

Пример 1. Вероятность промаха при стрельбе равна 0,2. Найти вероятности возможного числа появления промахов при 5 выстрелах.

Вероятность промаха , число испытаний . Искомые вероятности находим по формуле Бернулли:

.

Закон распределения имеет вид:

Х	0	1	2	3	4	5
Р	0,32768	0,4096	0,2048	0,0512	0,0064	0,00032

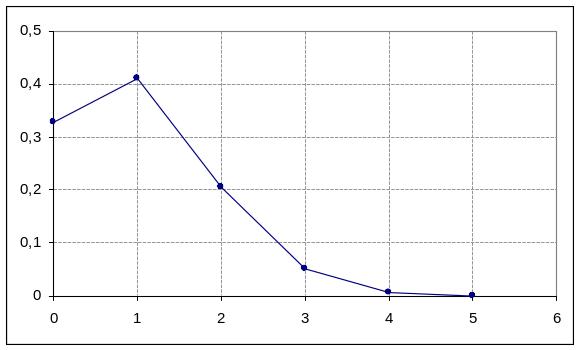и ли

Функция распределения – вероятность того, что случайная величина X примет значение меньшее x.

Свойства функции распределения:

1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей .

2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси, т.е. если 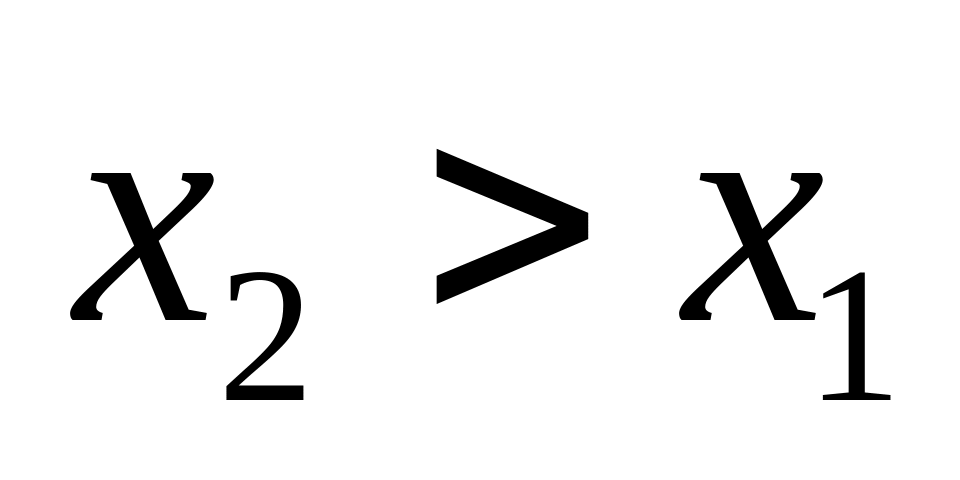, то .

3. , .

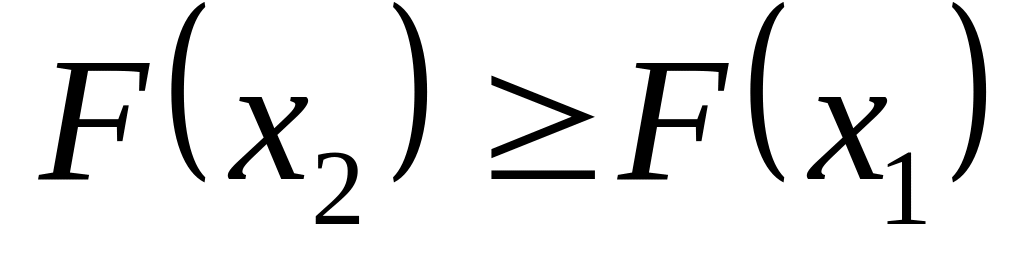4. Вероятность попадания случайной величины Х в интервал 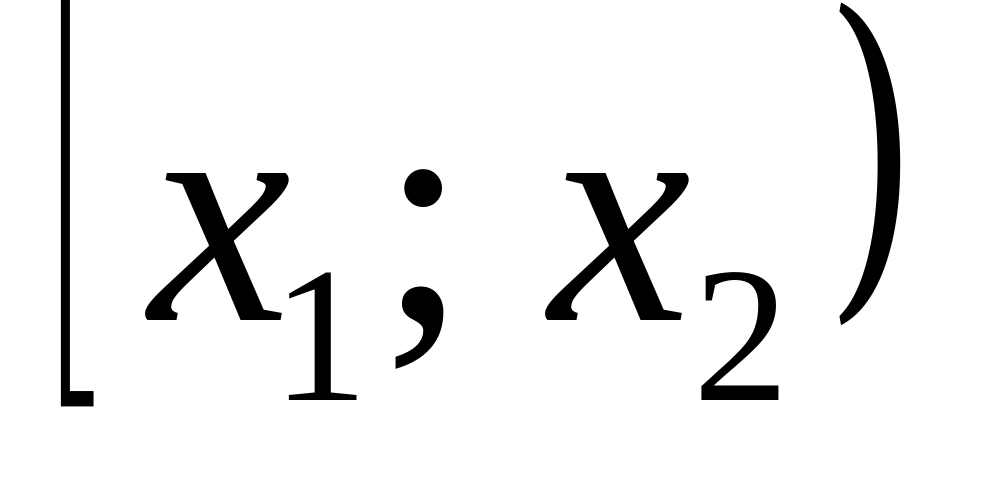равна приращению ее функции распределения на этом интервале: .

Составим функцию распределения в примере 1.

1. Если , то

2. Если , то

3. Если , то

4. Если , то

5. Если , то

6. Если , то

7. Если , то